Творческие задания на уроке математике для 5-6 классов. (работы учащихся). Творческое задание по математике 5 класс
Творческие задания по математике для учащихся 5—6-х классов
Разделы: Математика
Хорошо учит, хорошо помогает детям в учении не тот, кто знает науку, а тот, ктоумеет строить мост от незнания к знанию,кто видит и противоположный тёмный берегнезнания и непонимания.
Симон Соловейчик
Учебный материал по математике для 5-6 классов содержит очень много важных и сложных тем. Это и «Обыкновенные дроби и действия с ними», и «Десятичные дроби», и «Координатная прямая», «Положительные и отрицательные числа». В определённой мере понятия абстрактные и отличаются от количественных величин, изучаемых в начальной школе. Чтобы повысить эффективность усвоения данного материала, применяю в своей практике выполнение домашнего задания в виде творческих работ. Это написание сказок, составление кроссвордов, собирание пословиц по заданной теме. Ведь, чтобы написать сказку, необходимо увидеть в новом понятии или способе «изюминку», то чем оно отличается от других. Уяснить каковы его особенности, в чем его суть, а также обратить внимание на внешние признаки и характеристики. Иначе сказка не получится. В своём материале хочу представить содержание некоторых детских работ моих учеников, которые учатся сегодня, и которые уже закончили школу.
Сказка про десятичную дробь
Жило когда-то в «Математии» смешанное число, знаменатель которого был выражен единицей и нулями. Жило оно, не тужило, как вдруг в «Математию» прилетел огромный дракон. Он забирал себе то, что нравилось. И понравилось дракону у этого смешанного числа дробная черта и «круглый» знаменатель. Забрал всё это дракон и улетел. Заплакало смешанное число и отправилось к доброму математическому волшебнику. Волшебник сказал: «Не горюй, смешанное число. Взамен дробной черты дам я тебе компактную «запятую». И после этого все будут называть тебя десятичной дробью. И живёт теперь, не горюет эта десятичная дробь.
Садыкова Регина, ученица 5А класса
Сочинение «Пропажа»
Однажды пошли слухи, что у десятичной дроби украли запятую, а она сама сидит в пещере и плачет. Но когда случается где-нибудь беда, там сразу появляется Скуби-ду-би-ду, и всегда всех выручает. И вот однажды он пошел в эту пещеру, где сидела десятичная дробь. Десятичная дробь ему всё рассказала. Оказывается запятую украл её лучший друг – Шегги и теперь ей стыдно выходить из пещеры потому, что она стала обыкновенным числом. И тогда Скуби пошёл искать её друга Шегги. И вот, наконец, нашел его и увидел, где спрятана запятая. Она висела у него на шее. Тогда Скуби стал думать, как её спасти. И когда Шегги лёг спать, он пробрался и снял с шеи запятую, отнёс в пещеру и отдал десятичной дроби. И всё встало на свои места. Но Шегги проснувшись, не обнаружил на шее запятой, побежал скорее в пещеру, но там поджидал его сюрприз… Десятичная дробь позвала своих друзей и они наказали Шегги за воровство. Но как они его наказали для нас останется загадкой.
Андреева Анжелика, ученица 5Б класса
Сказка про параллельные прямые
Жили-были параллельные прямые a и b. Однажды они пошли в лес за ёлкой. Долго выбирали и наконец нашли. Хотели срубить, но оказалось, что не могут. Потому что они не пересекаются, а всегда идут прямо параллельно друг другу.
Федякова Елена, ученица 7Б класса
Миф: «Как возникли положительные и отрицательные числа»
Жили-были в математическом поселке АРАБЕЛЛА два числа-друга. Одного звали АЛЬ-ДЖЕБР, а другого АЛЬ-МУКАБАЛА. АЛЬ-ДЖЕБР – это число было очень порядочное и воспитанное, никогда не грубило другим числам, всегда слушалось своих родителей и ни разу в своей жизни не обмануло взрослого человека. А другое число, АЛЬ-МУКАБАЛА, было хулиганом и грубияном. Оно постоянно ввязывалось в драки, донимало всех подряд, начиная от маленьких и заканчивая большими, никогда не прислушивалось к советам других. За их поступки их начали называть так: АЛЬ-ДЖЕБР – положительным числом, а АЛЬ-МУКАБАЛА – отрицательным числом. И до наших дней дошёл этот миф. Учёные-математики придумали положительные и отрицательные числа в математической науке. Емельянова Анастасия, 5А класс
Сказка о координатной прямой
В одном графстве, которое называлось «Координатной прямой», жили числа. В центре города стоял главный дворец, в котором жил граф Нуль. Он решал важные вопросы. Население, которое проживало в этом графстве, называли числами. У каждого числа был домик, но не было адреса. И поэтому, когда числа ходили в гости друг к другу, то долго блуждали, ища нужный домик. Тогда жители начали жаловаться графу Нулю. Граф долго думал, как решить эту проблему. И, наконец, решил, что нужно написать адреса. Например, числа, которые живут справа, будут иметь адрес со знаком плюс (+1, + 2,…), а те, которые слева – со знаком минус (–1, – 2,…). С этого дня весь город жил тихо и никто не жаловался на жизнь.
Пинтилина Наталья, 6А класс
Сказка о координатной прямой
Жил на свете Плюсик и не было у него никогда друзей. Однажды Плюсик пошёл по белу свету друзей искать. Шёл Плюсик по лесу и видит, стоит Прямая под деревом и плачет. «Что же ты плачешь?» – спрашивает Плюсик. «Как же мне не плакать», – отвечает ему Прямая, - Не было у меня никогда друзей, скучно мне одной». «А я хожу по белу свету и ищу друзей. Пойдём со мною» – сказал Плюсик. Прямая очень обрадовалась и предложила: «Садись на меня я тебя прокачу. Здесь неподалёку город, пойдём туда». Плюсик согласился, и они отправились в путь. Долго они шли по лесу и заблудились. «Что же теперь делать, куда идти?», – сказал Плюсик. «Я вижу огонёк, пойдём туда», – предложила Прямая. Когда они подошли, то увидели, что на поляне стоял домик. Оказалось, что там жил Минус. Он был тоже одинокий, поэтому ребята взяли его с собой. Через некоторое время перед ними стоял город «Чиселко», в котором жили числа. Числа увидели Прямую, Плюсик и Минус и решили, что это враги. Но вскоре они поняли, что трое друзей пришли не воевать. Все они вскоре сдружились, и прямая предложила числам идти с ними. Числа согласились и стали рассаживаться на прямой. Каждый хотел сесть между Плюсиком и Минусом, и числа начали ссориться. «Я позову короля, он лучше, знает кому где сесть», – сказала троечка. Вскоре пришёл король Нуль. «Между Плюсиком и Минусом сяду я», – сказал король. Все жители замолчали и больше не ссорились. Король приказал, чтобы всех жителей рассадили на одинаковое расстояние друг от друга, а около короля сели Единицы – слуги его. За ними сели Двойки, потом Тройки, и так по очереди: 4, 5, 6. Получилось очень интересно: с правой стороны числа со знаком «+», а с левой со знаком «–». Королю это очень понравилось и он издал новый указ: «Отныне числа со знаком «+» будут положительными, а со знаком «–» – отрицательными. А ты, Прямая, со всеми числами будешь координатной». Так получилась координатная прямая.
Кокшарова Елизавета, 6А класс
Тема «Прямая и обратная пропорциональная зависимость» вызывает затруднение у шестиклассников при определении вида зависимости. Творческое задание по данной теме предполагает поиск пословиц, отражающих вид зависимости. Предварительно оговариваем, что пропорциональность в пословицах «удержать» затруднительно.
Пословицы, отражающие прямую зависимость:
- Чем дальше в лес, тем больше дров.
- Как аукнется, так и откликнется.
- Много снега, много хлеба.
- Кто рано встаёт, тому Бог подаёт.
- Как потопаешь, так и полопаешь.
- Выучишь правило, выполнишь верно задание.
- Кто много читает, тот много знает.
Пословицы, отражающие обратную зависимость:
- Тише едешь, дальше будешь.
- Мир строит, а война разрушает.
- Меньше народа, больше кислорода.
- Лето собирает, зима съедает.
- Было густо, стало пусто.
- Мал грех, да большую вину несёт.
- С большого грома – малый дождь.
- Меньше слов – больше дела.
Творческие работы учащихся
Аппликация из геометрических фигур. Автор: Голубева Алёна, 5Б класс.
Рисуем в координатной плоскости. Автор: Елисеева Анна, 6А класс.
Выполнение творческих работ позволяет повысить интерес к изучаемым темам даже у слабых учащихся. Как правило, задания подобного типа не вызывают у них трудностей, повышают интерес к математике и помогают сделать «нелюбимый» предмет доступным. Сильные же ученики, благодаря творческим работам, овладевают способностью переводить сложный математический материал в мир фантазий и красок. Данные задания позволяют показать красоту науки математики, её взаимосвязь с общечеловеческой культурой. Улучшают эмоциональное состояние учащихся. Повышают их интеллектуальное развитие и ведут к формированию всесторонне развитой личности.
xn--i1abbnckbmcl9fb.xn--p1ai
Творческие домашние задания по математике в 5-6 классах
Н.Н. Почикеева
Учитель математики
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 7 имени Героя Советского Союза Б.С. Левина»
г. Рославля Смоленской области
Творческие домашние задания по математике в 5-6 классах.
«Если ученик в школе не научился сам ничего творить, то и в жизни он всегда будет только подражать, копировать, так как мало таких, которые бы, научившись копировать, умели сделать самостоятельное приложение этих сведений»
(Л.Н. Толстой).
ФГОС ориентирован на становление ключевых характеристик выпускника, среди которых важными являются осознание ценности творчества, способность к творческой деятельности.
Поэтому одной из задач учителя является создание условий для развития и реализации творческого потенциала учащихся.
Для достижения данной задачи в 5-6 классах я использую разнообразные творческие домашние задания.
1. Создание задачи на заданную тематику. Учащиеся должны придумать задачу, решить ее и сделать к задаче соответствующую иллюстрацию.
Предлагаю создать «Осенние задачи», «Зимние задачи», «Весенние задачи», «Сказочные задачи» на изучаемые темы, «Вкусные задачи» на части, задачи «Проценты в нашей жизни», « Портрет нашего класса в процентах», «Великая Победа в задачах», «История нашего города в задачах».
Задачи, предложенные учениками, включаю в математические диктанты, самые интересные решаем в классной работе, обмениваются учащиеся задачами и решают их в домашней работе. Ребятам очень нравиться решать задачи своих товарищей.
Устраиваем конкурс самых лучших работ и победители «награждаются» пятеркой в журнал.
2. Создание ребусов.
Учащимся предлагается зашифровать слово. Это может быть название ранее не изученных тем из учебника. Предложенные учащимися ребусы, использую при объяснении нового материала по данной теме. Предлагаю зашифровать математические термины, фамилии математиков и рассказать о их вкладе в развитие математики, высказывания ученых о математике, пословицы и поговорки, связанные с математикой.
Создать ребус, в котором цифры заменены буквами. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы.
Создать цифровой ребус. В нем зашифрованы звездочками цифры от 0 до 9.
Использую ребусы, чтобы снять усталость, решаем их на занятиях математического кружка.
3. Сочинение математических сказок. Сочинение сказок, действующими лицами которых становятся математические объекты – также один из способов развития творческого воображения учащихся. При этом у детей развиваются умения наблюдать, сравнивать, обобщать. Вот что писал об этом В.А. Сухомлинский : «Создание сказок – один из самых интересных для детей видов поэтического творчества. Вместе с тем это важное средство для умственного развития… Если мне удавалось добиться, что ребенок, в развитии мышления которого встречались серьезные затруднения, придумал сказку, связал в своем воображении несколько предметов окружающего мира – значит можно сказать с уверенностью, что ребенок научился мыслить».
4. Сочинение стихов или частушек о математике, ее терминах.На недели математики устраиваем конкурс математических сказок, стихов и частушек.
5. Математические сочинения. В качестве тем предлагаю следующие темы: «Математика в моей семье», «Что было бы на земле без математики?», « Как дроби помогают человеку?» « Что изменилось для меня в изучении математики к концу 5, 6 класса?»
6. Создание кроссвордов и чайнвордов. Кроссворды и чайнворды хороши тем, что ученики должны дать грамотное определение тем математическим терминам, которые находятся в сетке данного кроссворда, чайнворда. В выполнении работы учащимся помогает справочник по теории, который мы ведем, начиная с 5 класса. В него записываем все изученные правила, определения, математические факты. В конце справочника создаем предметный указатель, для простоты его использования в дальнейшем в процессе повторения и создания кроссвордов.
7. Создание криптограмм. Криптограмма- это зашифрованное письмо. Чтобы разгадать криптограмму, надо расшифровать ключевые слова, приведенные к ней. Ученики составляют числовые выражения, которым ставят в соответствие буквы, значения выражений заносят в таблицу. Вычислив значения выражений, нужно расшифровать слово. Слово может быть из любой дисциплины. Кроме этого нужно сообщить интересные сведения о зашифрованном слове. Например, зашифровать «иллистый прыгун», сообщив о том, что это рыба, которая «бегает» по суше. Криптограммы предлагаю создать после изучения тем: действия с натуральными, целыми числами, действия с обыкновенными, десятичными дробями, смешанными числами.
Придуманные учениками криптограммы включаю в математические диктанты, предлагаю в качестве домашних заданий.
8. Создание анаграмм. Анаграммой называется слово, в котором поменяны местами все или несколько букв в сравнении с исходным словом. Решить анаграмму – означает определить исходное слово. Предлагаю зашифровать несколько слов так, чтобы слова были связаны закономерностью, а одно было лишним. Например,
ьпят, ост, ветядь (пять, сто, девять, пять и девять – цифры, сто – число – лишнее слово).
Созданные учениками анаграммы использую в паузах для смены видов деятельности.
9. Создание рисунков и аппликаций из одних окружностей, геометрических фигур после изучения тем «Окружность», «Прямоугольник», «Треугольник».
Создание рисунков к отдельным темам. Например, проиллюстрировать теорему о сумме углов треугольника, определение биссектрисы угла.
Создание рисунков «Симметрия в окружающем мире»
Устраиваем выставку работ и определяем победителей путем голосования.
10. Создание заданий «Лови ошибку» на заданную тему. Ученики разбиваются на группы, каждая группа должна придумать задания с решениями, содержащие ошибки и без ошибок. На уроке группы обмениваются своими заданиями, обсуждают предложенные задания, определяя в каких заданиях допущены ошибки и какие, а в каких нет. Затем делают взаимопроверку в группах. «Лови ошибку»- универсальный приём, активизирующий внимание учащихся.
11. Придумать математическую физкультминутку. Например, физкультминутка «Обыкновенная дробь»: ученик повторяет команды «числитель», «знаменатель», «черта дроби», а учащиеся повторяют соответствующие движения: «числитель» - руки вверх, «знаменатель» - руки вниз, «черта дроби» - руки в стороны. Предложенные физкультминутки используем во время динамических пауз на уроке.
12. Составить рисунок по координатам при изучении темы «Координатная плоскость». Ученики выполняют рисунок в координатной плоскости и указывают координаты точек, которые нужно последовательно соединить, чтобы получить задуманный рисунок. Учащиеся обмениваются заданиями и используют их в качестве домашних заданий: по выполненному рисунку указать координаты точек или построить по указанным координатам рисунок.
13. Придумать последовательности чисел по некоторой закономерности и продолжить ряд чисел. Придуманные последовательности разгадываем на кружке, включаем в разминку.
14. Создание «рассуждалок». Нужно задумать математическое понятие, а затем не называя его, рассуждать, где это понятие встречается, что с его помощью можно сделать, рассказать о его свойствах. Например, ученик загадал слово «окружность». Рассуждал так: это такая геометрическая фигура, интересная, красивая, у которой нет начала и нет конца. Эта фигура используется везде: в быту, в технике, архитектуре и других областях. Если пойдешь по нему, то все равно, когда-нибудь придешь туда, откуда ушел.
Таким образом, выполнение творческих работ позволяет повысить интерес к изучаемым темам даже у слабых учащихся. Как правило, задания подобного типа не вызывают у них трудностей, повышают интерес к математике и помогают сделать «нелюбимый» предмет доступным. Сильные же ученики, благодаря творческим работам, овладевают способностью переводить сложный математический материал в мир фантазий и красок. Данные задания позволяют показать красоту науки математики, её взаимосвязь с общечеловеческой культурой, улучшают эмоциональное состояние учащихся, повышают их интеллектуальное развитие и ведут к формированию всесторонне развитой, творческой личности.
infourok.ru
Творческие задания на уроке математике для 5-6 классов. (работы учащихся)
Творческие задания на уроке математике
для 5-6 классов.
Класс: 5
Творческое задание: составление задач на проценты.
Глава 5. Проценты.
Тема: Нахождение процента от числа и числа по ее проценту.
Творческое задание ориентировано на проверку знаний, умений и навыков учащихся.
Творческое задание используется на этапе актуализации знаний учащихся. Данную работу можно проводить в группах и индивидуально.
Учащиеся составляют задачи по данной теме на альбомных листах, красочно, с рисунками.
Данную форму работы можно применять как на уроке (закрепление, повторение, обобщение), так и в качестве домашней работы.
Приложение:
Класс: 5
Творческое задание: назовите слова, в которых имеются цифры и меры длины.
Творческое задание ориентировано на повышение интереса к знаниям, развитию познавательных способностей, развитию творческого воображения.
Данное творческое задание можно применять в начале урока, в качестве рефлексии, физминут пауз.
Например: группы по очереди называют слова, где имеются цифры или меры длины. (стол, столб, стоп, тритон, столовая, барометр, тонометр и т.д.).
Класс: 5-6
Творческое задание: составление ребусов.
Творческое задание ориентировано на развитие познавательной способности и творческого воображения. Ребусы учат логически рассуждать и нестандартно мыслить, развивает интерес к уроку. Применяются на различных этапах урока, по различным темам.
Чаще всего данное творческое задание использую на этапах повторения, закрепления и обобщения учебного материала.
Приложение:
Составил: учитель математики Ахметова Ирина Михайловна
(без категории, стаж по предмету 1 год)
www.metod-kopilka.ru
Творческие задания на уроках математики в 5-6 классах
Творческие задания на уроках математики в 5-6 классах
Самостоятельное приобретение учащимися новых знаний – творческий процесс. Большую помощь при этом оказывает введение в обучение творческих заданий.
Реальная творческая деятельность и творчество учащихся в учебном процессе – несколько разные вещи, поскольку последних творчеству всё-таки обучают. Поэтому в процессе творческой деятельности учащемуся может оказываться определенная помощь, например, через предъявление ему определённых эвристических предписаний. Осуществление таких предписаний может быть реализовано через творческие задания на уроках математики, через совместную деятельность педагога и учащихся. С дидактической точки зрения творческие задания представляют собой логически взаимосвязанные с друг другом задания, которые предлагаются учащимся в определенной последовательности, от простого к сложному. Итак, под творческим заданием понимают вид учебной деятельности, в которой учащиеся при непосредственном участии педагога целенаправленно усваивают знания, приобретают умения и навыки, которые в свою очередь используются в создании нового, посредством комбинации прошлого опыта. Применение творческих заданий на уроках математики способствует формированию убеждённости учащихся в том, что они не только успешно усваивают теоретический курс математики, но и сами создают нечто новое, несущее учебную нагрузку.
Среди наиболее применяемых заданий выделяют следующие:
составление учащимися задач по изученным темам программы с определённой целевой установкой на их содержание - экологическое, нравственное, связанное с местными проблемами и пр. (тем более, это важно в связи с тем, что содержание имеющихся в учебниках задач не всегда соответствует жизненным реалиям).
В 5 и 6 классе я предлагаю учащимся составить на нахождение части от целого и нахождение целого по значению его части. Ребята должны подобрать числа так, чтобы задача хорошо считалась. Заодно тренируем и устный счёт. Также можно предложить составить задачи по темам «Проценты», «Диаграммы».
сочинение сказок, рассказов по изученным разделам программы, что в методическом аспекте помогает решать и задачи целостного обобщения пройденной темы.
Это творческое задание можно предложить учащимся в 5 классе в теме «Геометрические фигуры», в 6 классе в теме «Положительные и отрицательные числа»
сочинение стихотворений на изученное правило или закон хорошо удаётся учащимся в 6 классе при изучении темы «Пропорции»
творческие практические задачи на геометрический материал программы (придумывание фигур, названий фигурам, рисунки, составление рассказов и сказок по графикам и диаграммам, как из учебных пособий, так и самостоятельно изображённым) хорошо давать детям в 5 и 6 классах. Мыслят они не тривиально, поэтому задания получаются оригинальные и весёлые. Учащиеся, выполняя рисунки, прослеживают связь математики с реальной жизнью.
написание сочинений по математике – высшая форма письменной работы, которая отражает опыт учащихся, их умение наблюдать, видеть, представлять, систематизировать, ясно излагать свои мысли, фантазировать. Такое задание стоит предлагать учащимся постарше. Во-первых, они уже имеют навык написания сочинений. Во-вторых, видят связь изученных тем и реальной жизни. Естественно, что данное задание носит необязательный характер.
Основную часть творческих заданий можно предлагать классу для домашнего выполнения, причём в некоторых случаях по желанию. После чего результаты творческих заданий просматриваются учителем, анализируются школьниками. Умелое использование разнообразных индивидуальных домашних заданий по математике способствует укреплению связи обучения с жизнью, развитию творческой самостоятельности и активности школьников в обучении, преодолению трафарета в задавании учебного материала на дом, развитию индивидуальных интересов учащихся, повышению качества обучения в школе. Таким образом, соблюдая все изложенные требования к домашним заданиям, учитель может создать оптимальные условия для развития творческой самостоятельности мышления школьников. Доклады учащихся оживляют урок, способствуют развитию способностей школьников, развивают интерес к математике. Готовя доклад, учащиеся приобретают навык работы с книгой, учатся выбирать главное из прочитанного текста и излагать материал лаконичным математическим языком. Несомненно, этот вид домашнего задания должен иметь больший удельный вес в старших классах, однако его можно практиковать и в средних классах.
Также следует отметить задания, выполняемые непосредственно на самом уроке:
это ряд заданий, выполняемых устно: можно использовать задания из тестов Айзенка; анаграммы и ребусы – их ребята с удовольствием подбирают сами.
задания на повторение учебного материала;
задания при объяснении нового материала: дети вполне могут подготовить несложную презентацию;
задания на выработку алгоритма действий, выработку умений и навыков, на закрепление знаний: алгоритм может быть оформлен с помощью «программы»;
задания для самостоятельных работ творческого характера: школьники придумывают задания для одноклассников;
задания с игровыми моментами.
Проводить весь учебный процесс, на уроке только используя задания творческого характера невозможно, необходимо чередовать творческую деятельность с деятельностью алгоритмической, стереотипной. В связи с этим в творческих заданиях предусмотрены тренинги, которые способствуют многократному повторению заданий одного типа для лучшего закрепления материала и быстрой наработки навыка.
infourok.ru
Творческое домашнее задание для 5 класса по теме «Правильные и неправильные дроби» - К уроку - Математика, алгебра, геометрия
Домашнее задание для 5 класса по теме:
«Правильные и неправильные дроби».
Цель работы:
закрепить умение сравнивать дроби;
находить часть от числа и число по его части;
поддержать интерес учащихся к математике интересным заданием.
Задание распечатывается каждому индивидуально на листе с двух сторон. Все вычисления должны выполняться детьми в тетради. Листочек-разукрашка закрашивается цветными карандашами, подписывается и сдается вместе с тетрадью на проверку. Лучшие работы на следующем уроке вывешиваются на доске.
Ребята очень любят выполнять такие задания. Это интересно, но требуют много времени для выполнения. Поэтому рекомендую давать такие задания на выходные дни.
Автор: Кусиди Анастасия Владимировна,
учитель математики,
МАОУ «Средняя школа №31»
г. Петропавловска-Камчатского
Ресурсы:
раскраска с сайта аllforchildren.ru
задания с учебника Виленкин Н.Я. «Математика 5 класс»
4
т ттттттттттттттттттттттттттттттттттттттттттттттттттт
Задания:
Какая из дробей больше или ?
Какая из дробей меньше или ?
Какая из точек лежит левее на координатном луче
А( ) или В( )?
Какая из точек лежит правее на координатном луче
К( ) или М( )?
Сложите числа 40 и числа 60.
Из числа 72 вычтите числа 21.
№ 1002 (учебник).
Таблица ответов:
| ответ | цвет | ответ | цвет | |
| красный | розовый | |||
| 60 | зеленый | 15 | голубой | |
| 56 | бордовый | фиолетовый | ||
| жёлтый | черный | |||
| серый | сиреневый | |||
| 33 | синий | 34 | коричневый |
На рисунке указаны номера заданий. Выполните задание в тетради, найдите ответ в таблице и соответствующим цветом разукрасьте рисунок.
Задания:
Какая из дробей больше или ?
Какая из дробей меньше или ?
Какая из точек лежит левее на координатном луче
А( ) или В( )?
Какая из точек лежит правее на координатном луче
К( ) или М( )?
Сложите числа 40 и числа 60.
Из числа 72 вычтите числа 21.
№ 1002 (учебник).
Таблица ответов:
| ответ | цвет | ответ | цвет | |
| красный | розовый | |||
| 60 | зеленый | 15 | голубой | |
| 56 | бордовый | фиолетовый | ||
| жёлтый | черный | |||
| серый | сиреневый | |||
| 33 | синий | 34 | коричневый |
На рисунке указаны номера заданий. Выполните задание в тетради, найдите ответ в таблице и соответствующим цветом разукрасьте рисунок.
pedsovet.su
Примеры творческих задании на уроках математики в 5 классе
Учитель математики СОШ №73Алимбаева Д.С.
Примеры творческих задании на уроках математики
в 5 классе
Степень развития ученика измеряется и оценивается его способностью самостоятельно приобретать новые знания и использовать их в учебной и практической деятельности. Самостоятельная работа занимает одно из ведущих мест среди факторов, способствующих формированию творческой активности учащихся, она позволяет глубоко усвоить знания, выработать и закрепить умения, превратить их в соответствующие навыки умственного труда.
Все виды самостоятельных работ, применяемых в учебном процессе, можно классифицировать по различным признакам:
- по дидактической цели
- по характеру учебной деятельности
- по степени самостоятельности
- по элементу творчества и т.д.
В зависимости от целей самостоятельные работы можно разделить на:
- обучающие
- тренировочные
- закрепляющие
- повторительные
- развивающие
- творческие
- контрольные.
Творческие самостоятельные работы вызывают у учащихся наибольший интерес. Здесь они открывают для себя новые стороны уже имеющихся знаний, учатся применять эти знания в неожиданных нестандартных ситуациях. Такой вид работ по математике служит формированию у учащихся интереса к предмету, воспитывает положительное отношение к предмету, развивает математическое мышление. Они предполагают достаточно высокий уровень самостоятельности.
Вот те виды самостоятельных творческих работ, которые я использую на уроках:
- решение задач и доказательство теорем нестандартным способом
- решение задач несколькими способами
- составление задач и примеров
- решение задач на нахождение и составление закономерностей
- задачи практического характера: разрезать, начертить, зашифровать, заполнить таблицу
- математические сочинения (стихи, сказки)
- исследовательские работы
- конструирование и моделирование.
А использование презентаций существенно помогает их организовать.
Самостоятельно составить задачи я обычно предлагаю ученикам в конце изучения темы. И даю определенную целевую установку на их содержание: экологическое, нравственное, сказочное или фантастическое. На мой взгляд, это важно в связи с тем, что содержание имеющихся в учебнике задач не соответствует жизненным реалиям. Наиболее интересные задачи я помещаю на слайд, оживляя красками.
Например:
Составление задач возможно:
- по краткой записи
- по формулам и уравнениям
- по графикам и диаграммам
- по заданному вопросу
- обратной данной или продолжающей данную.
Например.
К этой задаче можно поставить вопрос «Какова скорость ветра?» или «Чему равна собственная скорость бабочки?». При ответе на второй вопрос возможны 2 способа решения.
Приведу еще несколько примеров:
Важной особенностью нашего интеллекта является способность устанавливать взаимосвязи, находить закономерности. Именно эта способность дает нам возможность определить выражение лица собеседника, понять, что мы слушаем именно Вагнера, издали узнать друга по походке. Поиск закономерностей, а также составление своих подобных задач – один из любимых видов деятельности моих учеников. Предлагаю я такие задания в качестве разминки, обычно, в начале урока.
Примеры.
1.Определи закономерность и найди неизвестное число:
2. Какая буква должна быть следующей в этой последовательности:
O Д Т Ч П Ш С...
Для того, чтобы решить предложенную выше задачу, нужно понять, что же объединяет эти буквы. Можно проверить место букв в алфавите, форму букв, можно прикинуть так и эдак, и в конце концов придет озарение - последовательность представляет собой первые буквы слов один, два, три, четыре... Значит, следующая буква будет В.
3. Посмотрите на рисунок и скажите, какая фигура здесь лишняя.
Если ученик ответит, что круг, значит, он заметил, что это единственная фигура, которая не имеет прямых линий. Но если кто-то другой решил, что лишним является квадрат, ответ тоже будет правильным, так как он является здесь единственной фигурой, имеющей четыре прямых угла. Если учащемуся кажется, что в эту компанию не вписывается треугольник, то и он тоже прав - это единственный несимметричный объект. Сектор, в свою очередь, единственная из всех фигур, которая содержит и прямые линии, и кривые. Ну и, наконец, оставшаяся фигура единственная, которая имеет выемку. Короче говоря, каждая из фигур чем-то отличается от всех других. Но, в то же время, все они в равной степени имеют признаки, которые их объединяют. Главное при выполнении этого задания, привести аргументы, подтверждающие правильность выбора.
Написание математических сочинений, на мой взгляд, высшая форма письменной работы, которая отражает опыт учащихся, их умение наблюдать, видеть, представлять, систематизировать, ясно излагать свои мысли, фантазировать. Такую самостоятельную творческую работу я предлагаю обычно в конце четверти, разрешаю ее дополнить рисунками или кроссвордами.
Вот некоторые варианты тем для учащихся 5-6 классов:
- Как дроби помогают человеку.
- Простые числа.
- Мир треугольников.
- Симметричные фигуры.
- Прямоугольники различного вида.
- Как я подружился с модулем.
- Мои любимые задачи.
Например.
1. Сколькими способами вы можете разделить квадрат на четыре одинаковые части? Попытайтесь найти десять различных способов.
2. Из шести одинаковых палочек составить 4 равносторонних треугольника.
3. Определить вид треугольников (по сторонам и углам).
Сначала ученики называют виды треугольников, изображенных на картинке. Затем каждый из них получает карточку, на которой необходимо раскрасить треугольники одного вида одинаковым цветом.
В заключении хочу отметить, что урок был и остается основной формой организации учебно-воспитательного процесса. Сущность урока составляет организация учителем разнообразной работы учащихся по усвоению новых знаний, умений, навыков, в ходе которой осуществляется их воспитание и развитие. Современный урок - это урок, на котором учитель умело использует все возможные формы организации познавательной деятельности учащихся.
Один из потенциалов – это использование информационных технологий на уроках математики. Оно делает обучение более содержательным, зрелищным, способствует развитию самостоятельности и творческих способностей обучаемого, существенно повышает уровень индивидуализации обучения.
Моя задача как педагога - организовать педагогический процесс таким образом, чтобы у учащегося повышался интерес к знаниям, возрастала потребность в более полном и глубоком их усвоении, развивалась самостоятельность в работе. Чтобы в процессе обучения учащиеся не только овладевали установленной системой научных знаний, получали и отрабатывали учебные умения и навыки, но и развивали свои познавательные способности, накапливали опыт творческой деятельности, развивали творческое воображение.
Развитие творческой потенции ученика возможно только при непосредственном включении его в творческую деятельность. Никакой рассказ о творческой деятельности других людей и даже показ её не может научить творчеству. Русский классик Л.Н. Толстой считал: “Если ученик в школе не научился творить, то в жизни он будет только подражать, копировать”. Эти слова, на мой взгляд, актуальны и сейчас.
На тему: «Примеры творческих задании на уроках математики в 5 классе»
Уч.математики : Алимбаевва Д.С.
Караганда 2011-2012 у.г.
kzgov.docdat.com
Творческие задания по математике
Творческие задания по геометрии .
Задание 1.
Выполните построение по указанным координатам точек :
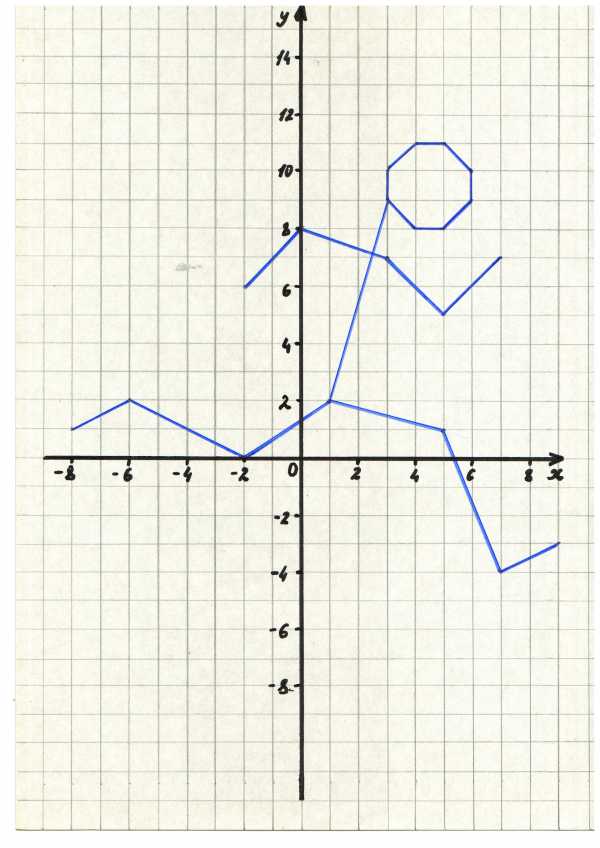
Бегун: (-8;1), (-6;2), (-2;0) ,(1;2), (5;1) ,(7;-4), (9;-3),
(-2;6), (0;8), (3;7) ,(5;5), (7;7)
(1;2) ,(3;9), (3;10) ,(4;11), (5;11),
(6;10), (6;9) ,(5;8) ,(4;8), (3;9)
Выполните построение в той последовательности, в которой указаны координаты точек.
Задание 2.
Выполните построение по указанным координатам точек :
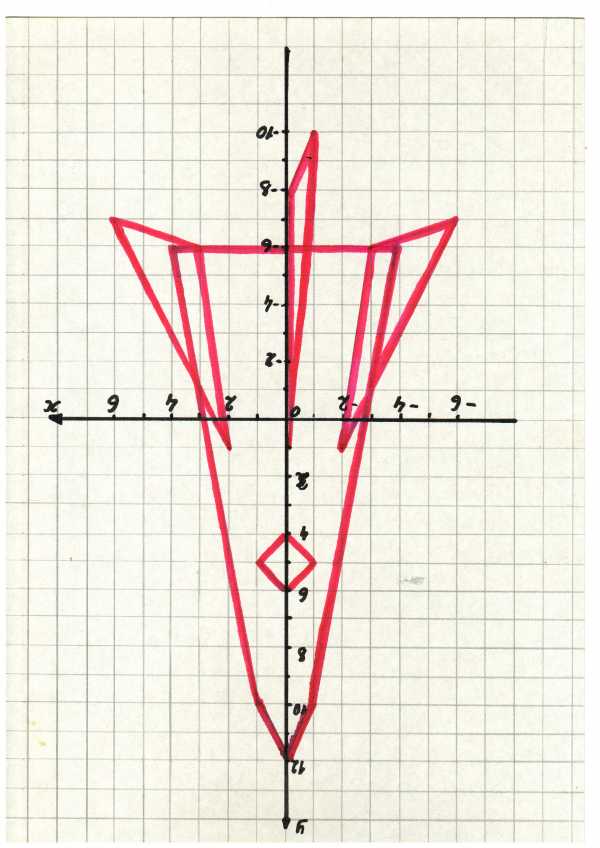
Ракета: (1;5), (0;6), (-1;5) ,(0;4), (0;-8) ,(-1;-10), (0;1),(0;-8)
(-4;-6), (-1;10), (0;12) ,(1;10), (4;-6),(-4,-6)
(-3;-6) ,(-6;-7), (-2;1) ,(-3;-6),
(2;1), (3;-6) ,(6;-7) ,(2;1)
Выполните построение в той последовательности, в которой указаны координаты точек.
Задание 3.
Выполните построение по указанным координатам точек :
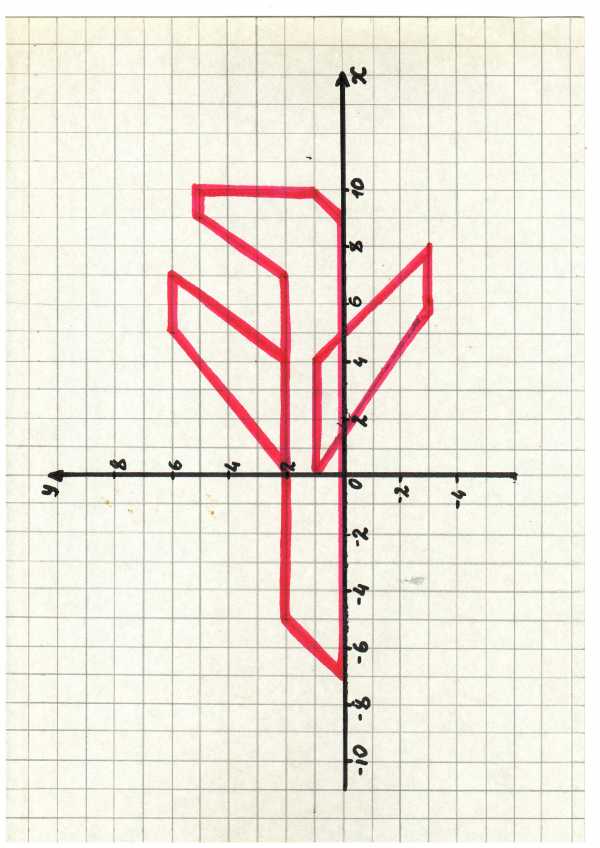
Ракета: (-7;0), (-5;2), (7;2) ,(9;5),
(10;5), (10;1), (9;0) ,(-7;0)
(0;2) ,(5;6), (7;6) ,(4;2),
(0;1), (6;-3) ,(8;-3) ,(4;1),(0;1)
Выполните построение в той последовательности, в которой указаны координаты точек.
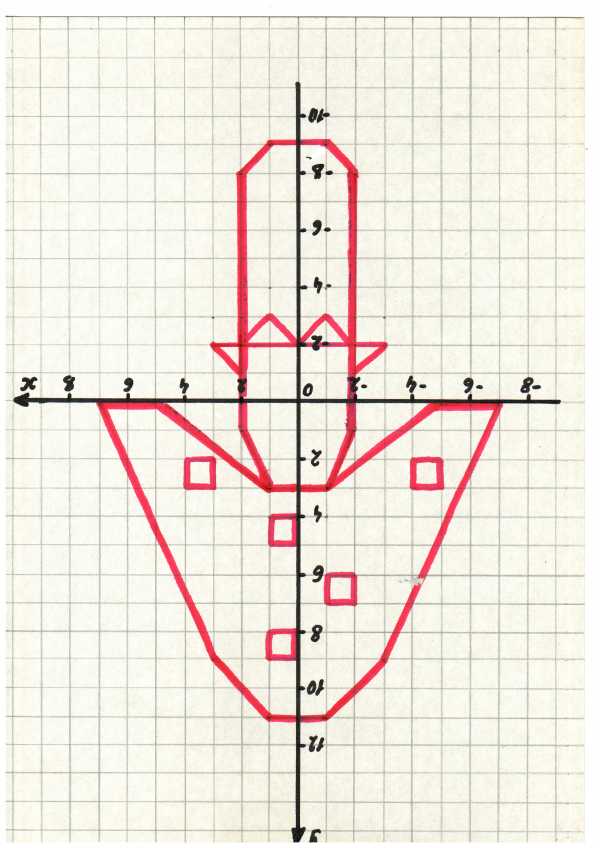
Задание 4.
Выполните построение по указанным координатам точек :
Мухомор: (-7;0), (-3;9), (-1;11) ,(1;11), (3;9) ,
(7;0), (5;0),(1;3), (-1;3) (-5;0) (-7;0)
(1;-9), (2;-8), (2;1) ,(1;3), (-1;3),(-2,1)
(-2;-8) ,(-1;-9), (1;-9) ,
(-2;-1), (-3;-2) ,(-2;-2) ,(-1;-3), (0;-2),
(1;-3), (2;-2), (3;-2), (2;-1),
(-2;6), (-2;7), (-1;7), (-1;6),
(3;2), (3;3), (4;3), (4;2),
(0;8), (0;9), (1;9), (1;8),
(-5;2), (-5;3), (-4;3), (-4;2),
(0;4),(0;5), (1;5), (1;4)
Выполните построение в той последовательности, в которой указаны координаты точек.
xn--j1ahfl.xn--p1ai