Математические головоломки. Математическая головоломка

в картинках и текстовые, для взрослых и детей

Разберите подборку головоломок вместе с детьми: «разомнете» мозги, весело проведете время и знание истории «прокачаете»! Мы выбрали интересные задачки, дошедшие до наших дней из «древности», и приближенные к «нашему» времени.

Папирус Ахмеса

Древние египтяне были не только опытными строителями пирамид, но и прекрасными математиками. Доказательством этому служит древнеегипетский папирус, автором которого был некий Ахмес. Как выяснили исследователи-египтологи, папирус Ахмеса — копия очень древнего математического сборника, составленного во времена фараона Аменемхета III (приблизительно 1853-1806 гг. до н.э.). Задач в сборнике много — ниже одна из них.

Задача о переправе

Не только древние египтяне упражнялись в решении задач на сообразительность. Историки обнаружили книгу, написанную на латыни, под названием «Задачи для развития молодого ума». Ирландский богослов, ученый и просветитель Алкуин, живший в IX веке, собрал в книге 53 задачи. Предлагаем одну из них — настолько «бородатую», что ее знают школьники во всем мире.

Как крестьянину перевезти все в целости и сохранности?

Печать царя Соломона

На гробнице мудрого легендарного библейского царя Соломона потомки изобразили знаменитую печать правителя.

Попробуйте сосчитать, сколько равносторонних треугольников изображено на печати.

Задача Фибоначчи о размножении кроликов

Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.

«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов».

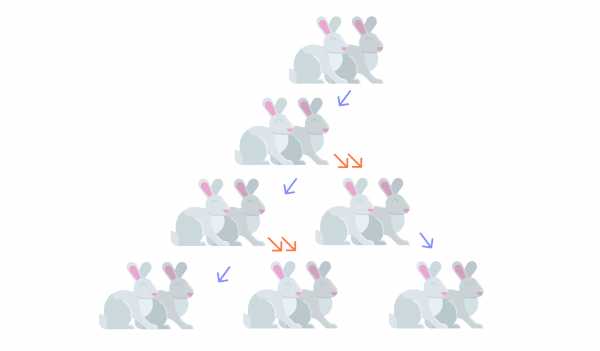
Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?

Смотреть подсказку и ответ

Вспомните последовательность Фибоначчи или запаситесь терпением — и считайте.

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …, …, …).

Ответ: 233 пары.

Задача Тартальи «Трудное наследство»

Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.

Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.

Как выполнить завещание?

Показать решение

Сам Тарталья предложил следующее решение. Для раздела имеющихся лошадей необходимо заимствовать еще одну, после чего их общее количество станет 18. Раздел этого количества даст 2, 6 и 9 лошадей, которых в сумме окажется 17. Одна лошадь из 18 оказалась как бы «лишней» — это заимствованная лошадь, которую следует вернуть владельцу после раздела имущества.

Можно решить головоломку и арифметическим способом: пропорцию 1/2 : 1/3 : 1/9 достаточно умножить на 18 и получится тот же результат.

Ответ: 2, 6 и 9 лошадей.

Головоломка Льюиса Кэрролла

Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику. Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:

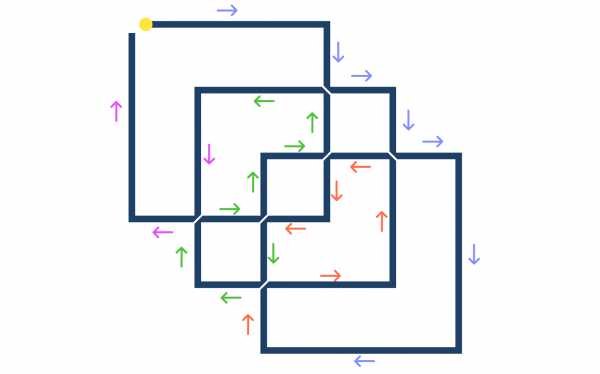
Нарисуйте фигуру, изображенную на рисунке.

Задача усложняется особыми условиями ее выполнения:

карандаш от бумаги отрывать нельзя;
дважды проводить карандашом в одном месте нельзя;
пересекать линии нельзя.

Смотреть решение

Ниже мы изобразили 2 варианта решения. Возможно, вам удастся найти и другие.

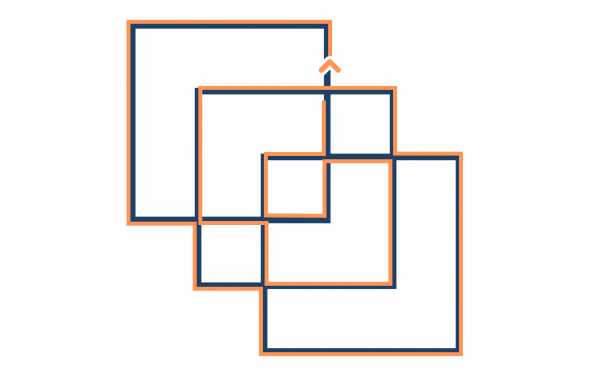
«Безумный разрез» Мартина Гарднера

Мартин Гарднер — известный американский писатель, математик-любитель, автор множества статей и книг по занимательной математике, научно-популярных этюдов, математических фокусов, головоломок и задач на сообразительность и множества других публикаций.

Предлагаем решить одну из самых популярных головоломок Гарднера.

Сделайте один разрез (или нарисуйте одну линию) — не обязательно, прямую — чтобы разделить нарисованную фигуру на две одинаковые части.

Сингапурская головоломка

Благодаря социальным сетям некоторые головоломки распространяются, как вирус, и становятся известными. Так случилось с головоломкой, которую телеведущий Кеннет Конг из Сингапура разместил на своей странице в фейсбуке, и вскоре ею поделились 4400 человек.

Альфред и Бернард только что познакомились с Шерил и хотят выяснить, когда у нее день рождения.

Шерил показала поклонникам 10 возможных дат:

Затем она показала Альфреду месяц своего рождения, а Бернарду — день.

Чтобы решить головоломку, друзья обменялись парой реплик:

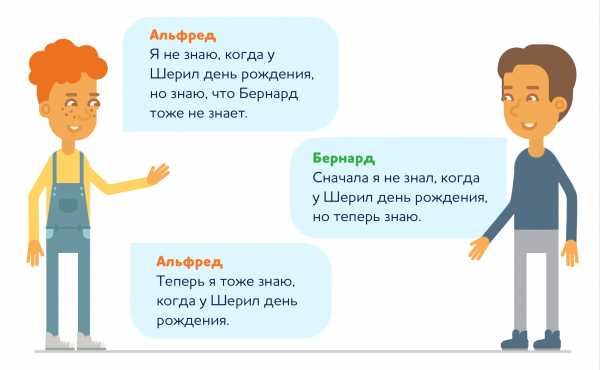
Так когда же у Шерил день рождения?

Смотреть решение и ответ

Даты находятся в промежутке от 14 до 19. Числа 18 и 19 встречаются по разу. Если день рождения в эти даты, то Бернард сразу бы сказал месяц.

Если Шерил сказала Альфреду, что родилась в мае или июне, значит, день рождения может быть 19 мая или 18 июня. Раз Альфред точно знает, что Бернард не знает ответ, значит, речь не о мае или июне. Остаются июль или август.

В июле и августе остались даты в диапазоне от 15 до 17, а 14 встречается дважды. Если бы день рождения был 14-го, то Бернард после реплики Альфреда еще не мог бы дать точного ответа. Значит, речь не о 14-ом. Остаются 16 июля, 15 августа и 17 августа.

Если бы Шерил сказала Альфреду, что родилась в августе, то после ответа Бернарда, Альфред не мог бы точно узнать дату рождения — ведь целых 2 даты приходятся на август.

Значит, Шерил родилась 16 июля.

Ответ: 16 июля.

Эту задачку Конгу показала племянница друга. Она же разыграла телеведущего, сказав, что головоломка предназначена для 10-летних школьников. Дебаты о том, как решить «простую» задачку, развернулись нешуточные. Спустя 2 дня, когда большинство участников сдались, выяснилось, что задача — олимпиадная, для 14-летних школьников.

Танграм

Согласно легенде, головоломка была создана несколько тысяч лет назад тремя древнекитайскими мудрецами для сына императора. Правитель хотел чтобы через простую игру его сын постиг начала математики, научился видеть окружающий мир глазами художника, стал терпеливым, как философ, и осознал, что сложные вещи состоят из простых.

Так появился «Ши-Чао-Тю» — квадрат, разрезанный на семь частей: 5 треугольников (2 больших, 2 маленьких, 1 средний), квадрат и параллелограмм.

Суть «свободной» игры в танграм - собирать из имеющихся деталей по принципу мозаики всевозможные фигурки: животных, птиц, человека, что угодно. Младшим дошкольникам предлагают простой вариант развивающей игры, когда фигурки танграма нужно просто наложить на готовый образец-ответ. Многие дети в 5-7 лет складывают модели из фигурок рядом с изображением-ответом, даже если размеры вырезанных фигур и деталей на картинке отличаются.

Танграм как головоломка обычно по силам ребенку начиная с 6-7 лет. Все так же — из элементов танграма нужно сложить готовую модель, но на карточке изображен лишь силуэт фигуры.

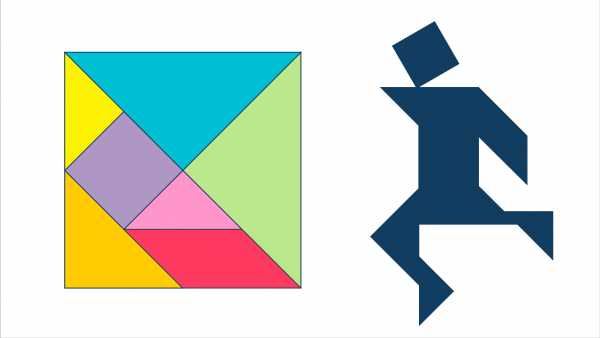
Вырежьте элементы танграма из бумажного, картонного или другого квадрата, и для начала предлагаем собрать одну из популярных фигурок — бегущего человека, как на рисунке выше.

Помните 2 правила головоломки: 1) необходимо использовать все 7 фигурок головоломки; 2) фигуры не должны накладываться друг на друга.

Среди поклонников танграма были Льюис Кэрролл и Наполеон Бонапарт. Считается, что именно «танграмом» назвал игру американский шахматист, изобретатель «пятнашек» и многих других головоломок, Самюэль Лойд. В 21 веке самые интересные проявления танграма встречаются в дизайне мебели, одежды, ландшафтном дизайне и архитектуре.

Со всеми головоломками успешно справились? Великие математики и логики мира гордились бы вами!

Делитесь ссылкой с друзьями — пусть и они проверят свои силы!

На ЛогикЛайк вас ждут более 2500 заданий на развитие логического, математического и пространственного мышления.

Задания по возрасту

logiclike.com

Математические головоломки | Логические задачи

Кирпич

Кирпич весит 1 килограмм плюс половину собственного веса. Сколько весит кирпич?

Муха

Два поезда, находящиеся на расстоянии 200 км, движутся навстречу друг другу со скоростью 50 км/ч каждый. Муха берёт старт с одного из поездов и летит по направлению к другому со скоростью 75 км/ч. Долетев до другого поезда, муха разворачивается и летит назад к первому. Так она летает туда и обратно, пока два поезда не сталкиваются, и насекомое погибает. Какое расстояние успела пролететь муха? Есть два способа решить эту задачку, один – простой, другой – тяжёлый.

Поезда

Из Бостона в Нью-Йорк выходит товарный поезд, двигаясь со скоростью 60 км/ч. Через 30 минут навстречу ему из Нью-Йорка в Бостон выходит пассажирский поезд, двигающийся со скоростью 80 км/ч. Который из поездов будет ближе к Нью-Йорку в момент встречи? (Попросите помощи школьников - они наверняка быстрее справятся с задачкой.)

Средняя скорость

Половину пути до города, находящегося на расстоянии 60 км, я проехал со средней скоростью 30 км/ч. С какой скоростью я должен ехать остаток пути, чтобы общая средняя скорость всего путешествия была бы 60 км/ч?

Проволка над экватором

Окружность Земли равна примерно 40000 км. Если протянуть проволоку над экватором вокруг Земли так, чтобы длина проволоки была бы только на 10 метров (0,01 км) длиннее окружности земли, сможет ли пролезть под этой проволокой блоха? Мышь? Человек?

Диофант

Мало что известно о жизни одного греческого математика из Александрии, которого называют родоначальником алгебры. Предполагается, что он жил в 3-м веке нашей эры. По рассказам, на его надгробии была высечена следующая эпитафия: «Детство Диофанта 1/6 жизни заняло; 1/12 жизни Диофант бороду растил; ещё 1/7 жизни Диофанта прошла до того, как он женился. Через 5 лет после свадьбы у Диофанта родился сын, который прожил только половину лет, что прожил его отец. А через 4 года после смерти сына умер Диофант.» Сколько лет прожил Диофант?

Папирус Ахмеса

В 1858 году Шотландский коллекционер Генри Райнд приобрел древнеегипетский папирус подписанный именем "Ахмес". Этот свиток папируса, шириной 33 см и длинной 5,25 метров, является копией ещё более древнего математического руководства, относящегося ко времени фараона Аменемхета III. Вот одна задача из этого древнейшего из математических сборников: Сто мер зерна надо поделить между пятью работниками так, чтобы второй получил настолько больше, чем первый, насколько третий больше, чем второй, и на столько же, насколько четвёртый больше, чем третий, и на столько же, насколько пятый больше, чем четвёртый. Сколько мер зерна должен получить каждый, если первый и второй работники вместе получат зерна в семь раз меньше, чем остальные три работника?

Сколько осталось до полуночи?

Через два часа до полуночи останется в два раза меньше, чем оставалось бы через час. Который сейчас час?

Стрелки часов

В полдень часовая, минутная и секундная стрелки часов совпадают в одной точке циферблата. Чуть больше, чем через час и пять минут, часовая и минутная стрелки совпадут снова. Найдите с точностью до миллисекунды время, когда они совпадут. Какой угол с ними будет в это время составлять секундная стрелка?

Бассейн

К бассейну подходят четыре трубы, по которым через краны можно контролировать скорость заполнения бассейна. Открыв первый кран, можно заполнить бассейн за 2 дня, второй – за 3 дня, третий – за 4 дня и четвёртый – за 6 часов. Сколько понадобится времени, чтобы наполнить бассейн, открыв все четыре крана одновременно?

Переезд через пустыню

Военный автомобиль с важным посланием должен пересечь пустыню. Однако полного бензобака хватает только на половину пути. В распоряжении военной базы имеется несколько таких автомобилей, и бензин можно перекачивать из одного бака в другой. Никакими канистрами и тросами они воспользоваться не могут. Как доставить сообщение, не бросая ни одного автомобиля в пустыне? (Попробуйте для наглядности проиграть ситуацию с игрушечными машинками.)

Авиотур

На одной далёкой планете есть только один аэропорт, находящийся на Севеном полюсе. В распоряжении аэропорта имеются 3 самолёта и неограниченное количество горючего. Бака самолёта хватает ровно до Южного полюса. Самолёты имеют возможность дозаправляться (перекачивать горючее из одного в другой), находясь в полёте. Как самолёт может облететь вокруг планеты так, чтобы все самолёты вернулись в аэропорт?

Мысленно разделите весь путь от полюса до полюса на три части (от Северного полюса до Южного полюса 3 части. И от Южного полюса до Северного полюса 3 части). Стратегия состоит в следующем. Шаг №1. Два смолета летят до первой трети пути, один из них дозаправляет второй и поворачивает назад, а второй продолжает лететь до отметки 2/3 пути. Шаг №2. Два самолета вновь вылетают из аэропорта до первой третьей пути. Один из них дозаправляет второй и поворачивает назад, а второй продолжает путь до отметки 2/3 пути. Шаг №3. На отметке 2/3 пути теперь два самолета, бензобаки каждого заполнены на 2/3. Один из них дозаправляет второй и отправляется назад до отметки в 1/3 пути, где его встречает и дозаправляет 1/3 своего топлива третий самолет из аэропорта, оба летят обратно в аэропорт. В это время самолет, бывший на отметке 2/3 пути, с полным баком летит дальше, насколько это возможно (он пролетит над Южным полюсом, обогнет планету и долетит до отметки последней 1/3 пути до аэропорта). Шаг №4. Остальные действия очевидны. Из аэропорта вылетает еще один самолет (на этот раз в противоположном направлении, то есть навстречу обогнувшему планету самолету), чтобы поделиться 1/3 своего топлива с основным самолетом и вместе с ним вернуться в аэропорт.

Волшебный пояс

Волшебный пояс, исполняющий желания хозяина, уменьшается в два раза в длину и в 3 раза в ширину после каждого исполненного желания. После исполнения трёх желаний площадь лицевой стороны стала 4 см2. Какова была изначальная длина ремня, если его изначальная ширина была 9 см?

Болдвил

У всех жителей города Болдвил разное количество волос на голове. Нет ни одного жителя, у которого было бы точно 518 волос на голове. Население города превышает число волос на голове любого из жителей Болдвил. Каково максимально возможное население города Болдвил?

Неверные жёны

Антрополог, изучавший племя в отдалённом уголке джунглей Амазонки, обнаружил странный обычай. Когда муж узнавал, что его жена изменяет, он должен был публично её казнить в полночь того же дня. Про любую женщину, изменяющую мужу, всегда знали все жители племени, кроме её мужа. Но мужу никто никогда не рассказывал об изменах его жены, потому что это противоречило кодексу чести. Тот же кодекс чести не позволял жёнам известить ту жену, чей муж был ей неверен. В противном случае она в тот же вечер пристрелила бы своего мужа. В день своего отъезда антрополог созвал всех представителей племени и объявил: «Я знаю, что в этом племени есть неверные жёны.» И на девятый день все неверные мужья были казнены. Сколько было неверных мужей?

Если принять количество неверных мужей за число «n», то количество неверных мужей, известных каждой жене неверного мужа, составляет «n-1» (потому что всем обо всём точно известно – только о верности собственного мужа приходится догадываться). Теперь построим следующую логическую цепочку. Предположим, что количество неверных мужей равно единице. Тогда всем, кроме одной, жёнам известно, что среди жителей есть один неверный муж, в то время как жена этого неверного мужа уверена, что все мужья верны своим жёнам. Как только она услышит, что среди жителей есть как минимум один неверный муж, она тут же поймёт, что может быть только её муж, поэтому в тот же вечер она его незадумываясь застрелит. А теперь представьте, что среди жителей есть два неверных мужа. Каждая жена таких неверных мужей уверена, что среди жителей есть только один неверный муж, поэтому ждёт, пока какая-нибудь из жён пристрелит своего мужа. Но в этот вечер никто никого не застрелил, а это может означать только одно: её СОБСТВЕННЫЙ муж ей ТОЖЕ неверен и является ВТОРЫМ неверным мужем в племени. Первая жена первого неверного мужа приходит к точно таким же выводам (она также ждала, что кто-то из жён застрелит своего мужа). Таким образом, обе оскорбленные жены в первый же вечер понимают, что их мужья им изменяют, и на следующий вечер (второго дня) пристреливают обоих мужей. Следуя этой логике, нетрудно догадаться, что количество неверных мужей «n» будут пристрелены в «n»-нный вечер.

1 = 2

Найдите ошибку в математических выкладках:

x = 2 x(x-1) = 2(x-1) x2-x = 2x-2 x2-2x = x-2 x(x-2) = x-2 x = 1

9 точек

Соедините 9 точек четырьмя прямыми линиями не отрывая руки и не обводя линий.

Девиз

В юности я обнаружил, что большой палец ноги рано или поздно проделывает дырку в носке. Поэтому я перестал надевать носки. Альберт Эйнштейн

brainden.com

Математические головоломки | Головоломки | Математика, логика, интеллект

Какой знак нужно поставить между цифрами 2 и 3, чтобы результат получился больше 2, но меньше 3?

Сложность головоломки: 3.

Разделите 10 апельсинов поровну между 12-ю мальчиками, при условии, что резать каждый апельсин можно не более чем на 3 равные части.

Сложность головоломки: 5.

Ответ

6 апельсинов режем пополам, а каждый из остальных — на 3 равные части, после чего даем каждому мальчику по половине и одной трети апельсина.

Полторы курицы за полтора дня снесут полтора яйца. Сколько яиц снесут 3 курицы за 4 дня?

Сложность головоломки: 4.

Щука весит столько, сколько весит килограмм и пол щуки. Какой вес щуки?

Сложность головоломки: 3.

Пошел отец с четырьмя сыновьями в лес по ягоды. Отец нашел 45 ягод, тогда, как ни один из его сыновей, не нашел ни одной ягоды. Раздал отец все собранные им ягоды детям и все снова разошлись по лесу. Когда собрались идти домой, оказалось, что один из сыновей нашел еще столько ягод, сколько получил от отца, второй нашел 2 ягоды, третий две съел, а четвертый, не найдя ни одной, съел половину того, что получил от отца, после чего оказалось, что во всех ягод стало поровну. Сколько ягод дал отец каждому из сыновей?

Сложность головоломки: 4.

У пастуха, который вел 70 быков, спросили: "Какую часть быков своего многочисленного стада ты ведешь?" Он ответил: "Я веду две трети от трети скота". Сколько быков было во всей череде?

Сложность головоломки: 4.

Ответ

Обозначим количество скота в стаде через x. Тогда по условию задачи получим равенство: 2/3 × (1/3 × x) = 70. Решив равенство получим ответ — 315 быков.

Из четырех жертвователей второй дал вдвое больше, чем первый, третий — втрое больше, чем второй, четвертый — вчетверо больше, чем третий, а все вместе дали 132. Сколько дал первый?

Сложность головоломки: 5.

Ответ

Пусть первый дал x. Тогда второй — 2x, третий — 3 (2x), четвертый — 4 (3 (2x)). Вместе же они пожертвовали: x + 2x + 3 (2x) + 4 (3 (2x)) = 132. Решив уравнение узнаем, что первый дал 4.

Несколько человек вместе покупают барана. Если каждый внесет по 5 монет, то не хватит к стоимость барана 45. Если каждый внесет по 7, то не хватит 3. Сколько людей и какова стоимость барана?

Сложность головоломки: 4.

Ответ

Пусть количество людей — x. А стоимость барана — y. Тогда составляем систему уравнений: y − 5x = 45, y − 7x = 3. Решив ее, получим ответ: 21 человек, а баран стоит 150.

Собака гонится за кроликом, который находится в 150 футах от нее. Она делает прыжок на 9 футов каждый раз, когда кролик прыгает на 7 футов. Сколько прыжков должна сделать собака, чтобы догнать кролика?

Сложность головоломки: 4.

Ответ

С каждым прыжком собака приближается к кролику на 9 − 7 = 2 фута. Поэтому, чтобы пройти расстояние в 150 футов, собаке нужно сделать 150/2 прыжков. Ответ: 75 прыжков.

На ферме выращивают кроликов и фазанов. Сейчас их столько, что во всех вместе 740 голов и 1980 ног. Сколько сейчас находится на ферме кроликов и фазанов?

Сложность головоломки: 4.

Ответ

Пусть x — количество фазанов, y — количество зайцев. Тогда 2x + 4y = 1980 и x + y = 740, отсюда x = 490, y = 250. То есть, на ферме есть 490 фазанов и 250 кроликов.

formula.co.ua

Математическая головоломка — Википедия с видео // WIKI 2

Математическая головоломка — задача занимательной математики с игровыми элементами (правилами возможных действий, иногда — сюжетом), требующая в большей степени сообразительности, нежели математической подготовки или специальных знаний.

Многие из общеизвестных головоломок в той или иной степени несут математическое содержание, например, в пентамино существенны формы и расположения фигур, а в судоку — свойства графов. Игру Конвея «Жизнь» и задачу построения фракталов можно также рассматривать в качестве математических головоломок, хотя игрок оперирует с ними только путём задания начальных конфигураций, а после того, как начальные условия установлены, правила головоломки определяют все дальнейшие изменения и ходы.

Многие головоломки хорошо известны, поскольку обсуждались Мартином Гарднером в колонке «Mathematical games» (рус. «Математические игры») в журнале Scientific American. Математические игры иногда используются для того, чтобы вовлечь студентов в изучение техники решения школьных задач[1].

Энциклопедичный YouTube

1/5
Просмотров:
15 628
4 784
1 144
20 527
5 149

Математическая головоломка 2
Загадочная математическая головоломка
Математическая головоломка, которая сбила с толку полмиллиона человек
Задача со спичками-3
Загадка со спичками с ответом

Содержание

Некоторые математические головоломки

Числа, арифметика и алгебра

Комбинаторные

Логика

Анализ и дифференцирование

Муравей на резиновой нити[en][5]

Вероятность

Мозаики, упаковки и разбиения

Игры на доске

Игры двух лиц

Шахматные задачи

Топология, узлы и теория графов

В области теории узлов и топологии интуитивно неочевидные выводыe часто становятся частями занимательной математики[23].

Механические головоломки

Примечания

↑ Kulkarni, D. Enjoying Math: Learning Problem Solving With KenKen Puzzles Архивировано 1 августа 2013 года., книга, посвященная головоломкам KenKen.
↑ Гарднер, 2009, Глава 10. Циклические числа, стр. 111—121
↑ Гарднер, 2009, Глава 33. Игра в 15 и другие головоломки, стр. 401
↑ Гарднер, 1999, Глава 6. «Икосаэдрическая игра» и «Ханойская башня», стр. 53
↑ Гарднер, 1990, Глава 9. Резиновый жгут и другие задачи, стр. 132
↑ Не игра!
↑ Гарднер, 1999, Глава 5. Парадоксы теории вероятности, стр. 50
↑ Гарднер, 2009, Глава 11. Геометрические задачи на разрезание фигур.
↑ Гарднер, 1999, Глава 40. Упаковка шаров, стр. 66
↑ Гарднер, 1974, Глава 7. Пентамино и полимино: пять игр и серия задач, стр. 95
↑ Гарднер, 1999, Глава 21. Кубики сома, стр. 176
↑ Гарднер, 1999, Глава 33. Механические головоломки, стр. 295
↑ Гарднер, 1999, Глава 1. Гексафлексагоны, стр. 10; Глава 17. Тетрафлексагоны, стр. 146
↑ Гарднер, 1999, Глава 13. Полимино, стр. 100
↑ Гарднер, 1999, Глава 32. Квадрирование квадрата, стр. 275
↑ Гарднер, 2009, Глава 38. Игра «Жизнь», стр. 458; Гарднер, 1988, Главы 20—22. Игра «Жизнь», стр. 287
↑ Гарднер, 2010, Глава 11. Покрытие «изуродованных» шахматных досок с помощью L-тримино, стр. 191
↑ Гарднер, 2009, Глава 16. Игра в солитёр, стр. 193
↑ Гарднер, 1999, Глава 8. Игра в Гекс, стр. 66
↑ Гарднер, 1999, Глава 14. Ним и Так-Тикс, стр. 119
↑ Гарднер, 2009, Глава 21. Восемь ферзей и другие занимательные задачи на шахматной доске, стр. 263
↑ Гарднер, 2009, Глава 35. Плоские графы, стр. 433—435
↑ Гарднер, 1999, Глава 22. Занимательная топология
↑ Гарднер, 1974, Глава 23. Топологические игры «Рассада» и «Брюссельская капуста», стр. 281

Литература

Мартин Гарднер. Математические головоломки и развлечения. — Москва: «Мир», 1999. — ISBN 5-03-003340-8.
Мартин Гарднер. Лучшие математические игры и головоломки. — Москва: АСТ,Астрель, 2009. — ISBN 978-5-17-058244-0 («Издательство АСТ»),978-5-271-23247-3 («Издательство Астрель»).
Мартин Гарднер. Математические новеллы. — Москва: «Мир», 1974.
Мартин Гарднер. Путешествие во времени. — Москва: «Мир», 1990.
Мартин Гарднер. Когда ты была рыбкой, головастиком — я…. — Москва: КоЛибри, 2010. — ISBN 978-5-389-00971-4.
Мартин Гарднер. Крестики-нолики. — Москва: «Мир», 1988. — ISBN 5-03-001234-6.

Ссылки

Эта страница в последний раз была отредактирована 6 ноября 2017 в 04:34.

wiki2.org

Математические головоломки для детей

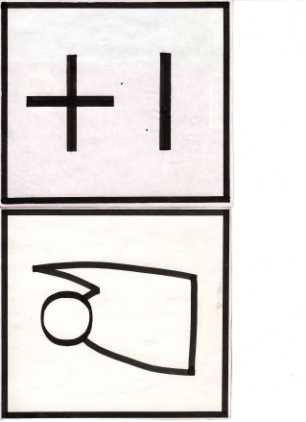
Математическая головоломка 1

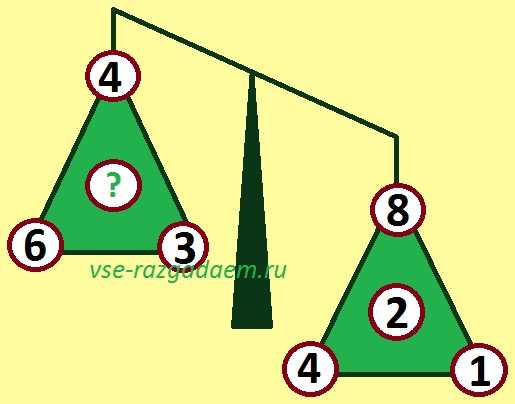
Первая математическая головоломка с числами (смотрите картинку № 1) предназначена для детей, которые уже освоили сложение и вычитание в пределах двадцати.

Задание для этой детской головоломки звучит так:

Реши эту арифметическую головоломку – подбери для кружочка с вопросом такое число, которое сможет уравновесить весы.

Упражняясь в решении таких математических головоломок, дети закрепляют свои навыки в счете, сложении и вычитании в пределах 20, а также развивают логическое мышление и смекалку.

Математическая головоломка для детей 2

Выполняя задание следующей головоломки, дети не только упражняются в счете в пределах двадцати, развивают восприятие, внимание, но также закрепляют умение оперировать такими понятиями, как цвет, размер, расположение на рисунке, форма (геометрические фигуры: круг, треугольник, квадрат).

Задания к данной головоломке могут быть такими.

Рассмотри внимательно картинку и ответь на следующие вопросы:

Какие фигуры здесь изображены и какого цвета?

Сколько всего квадратов (кругов, треугольников) на рисунке?

Сколько всего фигур на картинке?

Сколько фигур красного (синего, фиолетового) цвета?

Сколько фигур закрашенных в красный (фиолетовый, синий) цвет?

Сколько всего не закрашенных фигур?

Найди большой красный треугольник. Какая фигура находится внутри него, слева, сверху, за ним и так далее.

Примечание: подобных вопросов можно задать еще много. Все будет зависеть от того, какие понятия вы хотите закрепить с детьми.

Математическая головоломка для детей 3

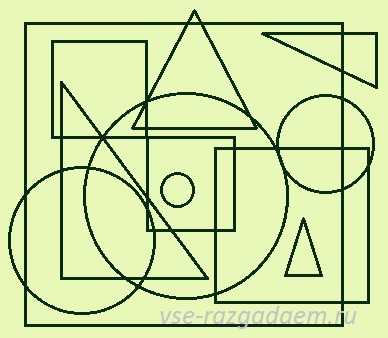
Эта математическая головоломка подобна предыдущей. Но, как вы можете заметить, здесь делается акцент только на количество, форму и расположение геометрических фигур. Так что все вопросы, исключая вопросы про цвет и наличие закрашенных фигур, из прошлой головоломки подойдут и к данной.

С одной стороны рисунок к этой головоломке выглядит проще, но решать детям ее даже труднее, так как вычленить определенные фигуры из более однородной массы изображенных объектов сложнее.

Для совсем маленьких деток, которые не умеют считать, рекомендую головоломку для малышей «Путаница».

vse-razgadaem.ru

Доклад «Математические головоломки»

Муниципальное образование Ленинградский район

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №10

х. Куликовского

муниципального образования

Ленинградский район

ДОКЛАД

«Математические головоломки»

Работу выполнил

ученик 7 класса

Сердюк Сергей

х. Куликовский

2012 г

Головоломка — это задача или загадка для решения которой требуется проявить сообразительность и знания в области, о которой идет речь в головоломке. Головоломки – игрушки на все времена. С самых давних пор умельцы изготавливали подобные забавы, отличающиеся многообразием вариантов решения. В наше время очень много людей увлекаются головоломками. Они любимы не только детьми, но и взрослыми. Это способ отвлечения от повседневных проблем и направлены на развитие различных мыслительных процессов - сопоставление, обобщение, установление последовательности, определение отношений «целое» - «часть».

Как же появились головоломки? Появились они очень давно. Логические головоломки находят в древнегреческих манускриптах, на стенах египетских пирамид и во многих других исторических документах и памятниках. В конце IX века наблюдался расцвет в истории головоломок, что закономерно связано с ростом уровня образования в то время и уменьшением религиозной нетерпимости к различного рода наукам. В тоже время в Европе появляется и первая книга головоломок ирландского просветителя Алкунина "Задачи для развития молодого ума".

В конце XIX начале XX веков, благодаря американцу Сэму Лойду и англичанину Генри Дьюдени головоломки получают очень широкое распространение. Они появляются во многих популярных изданиях и становятся популярны среди населения. Сэм Лойд считается автором такой известной и популярной игры как Пятнашки. Одно время игра была столь любима, что многие работодатели были вынуждены издать приказы, запрещающие приносить ее на рабочее место.

До 1974 года в мире головоломок наблюдалось некоторое затишье пока на сцену не вышел венгр Эрне Рубик со своим всемирно известным изобретением. Но Кубик Рубика, который изначально вовсе не был головоломкой,стал не только игрушкой, но и объектом серьезного исследования инженеров и математиков.

Известно, что число возможных состояний Кубика Рубика равно 43 252 003 274 489 856 000 комбинаций. Но, несмотря на такое огромное число было доказано, что из любого из этих состояний головоломка может быть собрана не более чем за 20 ходов. Этот алгоритм решения головоломки был назван "Алгоритмом Бога".

Индустрия головоломок в современном мире развивается огромными темпами. На рынке постоянно появляются новые игры и конструкции, призванные тренировать мозг человека и держать его в тонусе. Появился даже вид спорта — Пазлспорт — соревнование на скоростное решение головоломок. А с 1992 года проводятся регулярные Чемпионаты Мира по решению головоломок.

Виды головоломок

Существует огромное количество головоломок различного вида и какой-либо общепринятой классификации нет.

Устные головоломки. Это головоломки, условие которых может быть передано в устной речи без привлечения каких-либо дополнительных предметов. К ним можно отнести: загадки, шарады, парадоксы, игру данетки

Головоломки с предметами. Это головоломки, в которых активно используются обычные бытовые предметы: головоломки со спичками, монетами, карточные головоломки.

Следующий вид головоломок — это механические головоломки. Механические головоломки — это класс головоломок, которые специально были изготовлены как головоломки. Это всевозможные проволочные головоломки, головоломки типа Кубика Рубика, пазлы, пентамино и др.

Еще одним отдельным видом можно выделить печатные головоломки. Это те головоломки, для которых необходима бумага и карандаш. Они могут быть напечатаны или нарисованы. К таким головоломкам относятся, самые разнообразные кроссворды, ребусы, головоломка какуро, японские кроссворды, различные геометрические и математические головоломки и многие другие.

С развитием компьютеров стали активно развиваться компьютерные головоломки. В первую очередь туда попали устные и печатные головоломки, а также стали активно создаваться программы-головоломки: флеш-головоломки, пасьянсы и другие.

Для многих людей знакомство с головоломками начиналось с “пятнашек” – так часто называют известную игру “15”. С пятнашек начинается история игр с дыркой – головоломок, в которых фишки перемещаются по игровому полю за счёт того, что одно из мест на поле свободно. У “пятнашек” есть множество родственников, которые как раз и образовывают целый раздел этих головоломок. До “пятнашек” никакая другая головоломка таким успехом не пользовалась. Вскоре после своего появления на свет коробочка с цифрами 15 на крышке пересекла океан, быстро распространилась во всех европейских странах и поучила новое имя “такен”.

Знаменитейшая головоломка нашего времени – кубик Рубика – начала своё победное шествие по свету с 1978 года, когда с ней впервые ознакомились математики на Международном математическом конгрессе в Хельсинки. Лишь несколько кубиков увезли математики с конгресса, но это стало начальным толчком лавинного распространения игрушки по всему миру. Практически каждый может собрать одну грань кубика Рубика, но чтобы составить его полностью, часто приходится серьёзно задуматься. Собирая первую грань (или первый слой), можно не заботиться об остальных, но когда остаётся поменять местами последние несколько кубиков, очень легко всё испортить и начинать сначала. Мы рассмотрели лишь малую часть замечательных головоломок, которые придумали математики разных времён, но если когда-нибудь ещё и изобретут головоломку более популярную, чем, например, игра “15”, то известней знаменитого кубика Рубика наверняка – нет!

mognovse.ru

Математическая головоломка — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Некоторые математические головоломки

Числа, арифметика и алгебра

Комбинаторные

Логика

Анализ и дифференцирование

Вероятность

Мозаики, упаковки и разбиения

Игры на доске

Игры двух лиц

Шахматные задачи

Топология, узлы и теория графов

Механические головоломки

Напишите отзыв о статье "Математическая головоломка"

Примечания

↑ Kulkarni, D. [www.matholympiad.info/Documents/TeachingWithKenKen.pdf Enjoying Math: Learning Problem Solving With KenKen Puzzles], книга, посвященная головоломкам KenKen.
↑ Гарднер 2009, Глава 10. Циклические числа, стр. 111—121
↑ Гарднер 2009, Глава 33. Игра в 15 и другие головоломки, стр. 401
↑ Гарднер 1999, Глава 6. «Икосаэдрическая игра» и «Ханойская башня», стр. 53
↑ Гарднер 1990, Глава 9. Резиновый жгут и другие задачи, стр. 132
↑ Не игра!
↑ Гарднер 1999, Глава 5. Парадоксы теории вероятности, стр. 50
↑ Гарднер 2009, Глава 11. Геометрические задачи на разрезание фигур.
↑ Гарднер 1999, Глава 40. Упаковка шаров, стр. 66
↑ Гарднер 1974, Глава 7. Пентамино и полимино: пять игр и серия задач, стр. 95
↑ Гарднер 1999, Глава 21. Кубики сома, стр. 176
↑ Гарднер 1999, Глава 33. Механические головоломки, стр. 295
↑ Гарднер 1999, Глава 1. Гексафлексагоны, стр. 10; Глава 17. Тетрафлексагоны, стр. 146
↑ Гарднер 1999, Глава 13. Полимино, стр. 100
↑ Гарднер 1999, Глава 32. Квадрирование квадрата, стр. 275
↑ Гарднер 2009, Глава 38. Игра «Жизнь», стр. 458; Гарднер 1988, Главы 20—22. Игра «Жизнь», стр. 287
↑ Гарднер 2010, Глава 11. Покрытие «изуродованных» шахматных досок с помощью L-тримино, стр. 191
↑ Гарднер 2009, Глава 16. Игра в солитёр, стр. 193
↑ Гарднер 1999, Глава 8. Игра в Гекс, стр. 66
↑ Гарднер 1999, Глава 14. Ним и Так-Тикс, стр. 119
↑ Гарднер 2009, Глава 21. Восемь ферзей и другие занимательные задачи на шахматной доске, стр. 263
↑ Гарднер 2009, Глава 35. Плоские графы, стр. 433—435
↑ Гарднер 1999, Глава 22. Занимательная топология
↑ Гарднер 1974, Глава 23. Топологические игры «Рассада» и «Брюссельская капуста», стр. 281

Литература

Мартин Гарднер. Математические головоломки и развлечения. — Москва: «Мир», 1999. — ISBN 5-03-003340-8.
Мартин Гарднер. Лучшие математические игры и головоломки. — Москва: АСТ,Астрель, 2009. — ISBN 978-5-17-058244-0 («Издательство АСТ»),978-5-271-23247-3 («Издательство Астрель»).
Мартин Гарднер. Математические новеллы. — Москва: «Мир», 1974.
Мартин Гарднер. Путешествие во времени. — Москва: «Мир», 1990.
Мартин Гарднер. Когда ты была рыбкой, головастиком — я…. — Москва: КоЛибри, 2010. — ISBN 978-5-389-00971-4.
Мартин Гарднер. Крестики-нолики. — Москва: «Мир», 1988. — ISBN 5-03-001234-6.

Ссылки

Отрывок, характеризующий Математическая головоломка

Жюли собиралась на другой день уезжать из Москвы и делала прощальный вечер. – Безухов est ridicule [смешон], но он так добр, так мил. Что за удовольствие быть так caustique [злоязычным]? – Штраф! – сказал молодой человек в ополченском мундире, которого Жюли называла «mon chevalier» [мой рыцарь] и который с нею вместе ехал в Нижний. В обществе Жюли, как и во многих обществах Москвы, было положено говорить только по русски, и те, которые ошибались, говоря французские слова, платили штраф в пользу комитета пожертвований. – Другой штраф за галлицизм, – сказал русский писатель, бывший в гостиной. – «Удовольствие быть не по русски. – Вы никому не делаете милости, – продолжала Жюли к ополченцу, не обращая внимания на замечание сочинителя. – За caustique виновата, – сказала она, – и плачу, но за удовольствие сказать вам правду я готова еще заплатить; за галлицизмы не отвечаю, – обратилась она к сочинителю: – у меня нет ни денег, ни времени, как у князя Голицына, взять учителя и учиться по русски. А вот и он, – сказала Жюли. – Quand on… [Когда.] Нет, нет, – обратилась она к ополченцу, – не поймаете. Когда говорят про солнце – видят его лучи, – сказала хозяйка, любезно улыбаясь Пьеру. – Мы только говорили о вас, – с свойственной светским женщинам свободой лжи сказала Жюли. – Мы говорили, что ваш полк, верно, будет лучше мамоновского. – Ах, не говорите мне про мой полк, – отвечал Пьер, целуя руку хозяйке и садясь подле нее. – Он мне так надоел! – Вы ведь, верно, сами будете командовать им? – сказала Жюли, хитро и насмешливо переглянувшись с ополченцем. Ополченец в присутствии Пьера был уже не так caustique, и в лице его выразилось недоуменье к тому, что означала улыбка Жюли. Несмотря на свою рассеянность и добродушие, личность Пьера прекращала тотчас же всякие попытки на насмешку в его присутствии. – Нет, – смеясь, отвечал Пьер, оглядывая свое большое, толстое тело. – В меня слишком легко попасть французам, да и я боюсь, что не влезу на лошадь… В числе перебираемых лиц для предмета разговора общество Жюли попало на Ростовых. – Очень, говорят, плохи дела их, – сказала Жюли. – И он так бестолков – сам граф. Разумовские хотели купить его дом и подмосковную, и все это тянется. Он дорожится. – Нет, кажется, на днях состоится продажа, – сказал кто то. – Хотя теперь и безумно покупать что нибудь в Москве. – Отчего? – сказала Жюли. – Неужели вы думаете, что есть опасность для Москвы? – Отчего же вы едете? – Я? Вот странно. Я еду, потому… ну потому, что все едут, и потом я не Иоанна д'Арк и не амазонка. – Ну, да, да, дайте мне еще тряпочек. – Ежели он сумеет повести дела, он может заплатить все долги, – продолжал ополченец про Ростова. – Добрый старик, но очень pauvre sire [плох]. И зачем они живут тут так долго? Они давно хотели ехать в деревню. Натали, кажется, здорова теперь? – хитро улыбаясь, спросила Жюли у Пьера. – Они ждут меньшого сына, – сказал Пьер. – Он поступил в казаки Оболенского и поехал в Белую Церковь. Там формируется полк. А теперь они перевели его в мой полк и ждут каждый день. Граф давно хотел ехать, но графиня ни за что не согласна выехать из Москвы, пока не приедет сын. – Я их третьего дня видела у Архаровых. Натали опять похорошела и повеселела. Она пела один романс. Как все легко проходит у некоторых людей! – Что проходит? – недовольно спросил Пьер. Жюли улыбнулась. – Вы знаете, граф, что такие рыцари, как вы, бывают только в романах madame Suza. – Какой рыцарь? Отчего? – краснея, спросил Пьер. – Ну, полноте, милый граф, c'est la fable de tout Moscou. Je vous admire, ma parole d'honneur. [это вся Москва знает. Право, я вам удивляюсь.] – Штраф! Штраф! – сказал ополченец. – Ну, хорошо. Нельзя говорить, как скучно! – Qu'est ce qui est la fable de tout Moscou? [Что знает вся Москва?] – вставая, сказал сердито Пьер. – Полноте, граф. Вы знаете! – Ничего не знаю, – сказал Пьер. – Я знаю, что вы дружны были с Натали, и потому… Нет, я всегда дружнее с Верой. Cette chere Vera! [Эта милая Вера!] – Non, madame, [Нет, сударыня.] – продолжал Пьер недовольным тоном. – Я вовсе не взял на себя роль рыцаря Ростовой, и я уже почти месяц не был у них. Но я не понимаю жестокость… – Qui s'excuse – s'accuse, [Кто извиняется, тот обвиняет себя.] – улыбаясь и махая корпией, говорила Жюли и, чтобы за ней осталось последнее слово, сейчас же переменила разговор. – Каково, я нынче узнала: бедная Мари Волконская приехала вчера в Москву. Вы слышали, она потеряла отца? – Неужели! Где она? Я бы очень желал увидать ее, – сказал Пьер. – Я вчера провела с ней вечер. Она нынче или завтра утром едет в подмосковную с племянником. – Ну что она, как? – сказал Пьер. – Ничего, грустна. Но знаете, кто ее спас? Это целый роман. Nicolas Ростов. Ее окружили, хотели убить, ранили ее людей. Он бросился и спас ее… – Еще роман, – сказал ополченец. – Решительно это общее бегство сделано, чтобы все старые невесты шли замуж. Catiche – одна, княжна Болконская – другая. – Вы знаете, что я в самом деле думаю, что она un petit peu amoureuse du jeune homme. [немножечко влюблена в молодого человека.] – Штраф! Штраф! Штраф! – Но как же это по русски сказать?..

Когда Пьер вернулся домой, ему подали две принесенные в этот день афиши Растопчина. В первой говорилось о том, что слух, будто графом Растопчиным запрещен выезд из Москвы, – несправедлив и что, напротив, граф Растопчин рад, что из Москвы уезжают барыни и купеческие жены. «Меньше страху, меньше новостей, – говорилось в афише, – но я жизнью отвечаю, что злодей в Москве не будет». Эти слова в первый раз ясно ыоказали Пьеру, что французы будут в Москве. Во второй афише говорилось, что главная квартира наша в Вязьме, что граф Витгснштейн победил французов, но что так как многие жители желают вооружиться, то для них есть приготовленное в арсенале оружие: сабли, пистолеты, ружья, которые жители могут получать по дешевой цене. Тон афиш был уже не такой шутливый, как в прежних чигиринских разговорах. Пьер задумался над этими афишами. Очевидно, та страшная грозовая туча, которую он призывал всеми силами своей души и которая вместе с тем возбуждала в нем невольный ужас, – очевидно, туча эта приближалась. «Поступить в военную службу и ехать в армию или дожидаться? – в сотый раз задавал себе Пьер этот вопрос. Он взял колоду карт, лежавших у него на столе, и стал делать пасьянс.

wiki-org.ru