Задачи на масштаб с ответами 6 класс: Самостоятельная работа по математике на тему «Масштаб» (6 класс)

Самостоятельная работа по теме «Масштаб» с образцами решений задач.

Самостоятельная работа по теме «Масштаб» с образцами решений задач.

Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости

Библиотека

▪Методические разработки

▪Занятия

Материал опубликовала

5

#6 класс #Математика #Методические разработки #Занятие #Учитель-предметник #Школьное образование #УМК «Сферы» Е. А. Бунимовича

Нажмите, чтобы скачать публикацию
в формате MS WORD (*.DOC)

Размер файла: 21.52 Кбайт

24.12.2020 Самостоятельная работа по теме «Масштаб»

Опубликовано 23.12.20 в 23:25

Чтобы написать комментарий необходимо авторизоваться.

Закрыть

Тест по математике Масштаб 6 класс

Тест по математике Масштаб для учащихся 6 класса с ответами. Тест состоит из 2 вариантов, в каждом варианте по 8 заданий.

1 вариант

1. Как правильно записать масштаб карты, если один сантиметр на карте соответствует двум миллионам сантиметров на местности?

1) 1 : 200 000
2) 2 000 000 : 1
3) 1 : 2 000 000
4) 1 : 2000

2. Расстояние, равное 60 м, изображено на плане отрезком, длиной 4 см. Определите масштаб плана.

1) 4 : 60
2) 1 : 15
3) 4 : 6000
4) 1 : 1500

3. На одном чертеже деталь изображена в масштабе 1 : 5, а на другом — та же деталь в масштабе 5 : 1. На каком чертеже изображение детали получилось увеличенным в 5 раз по сравнению с действительными размерами детали?

1) на первом в масштабе 1 : 5
2) на втором в масштабе 5 : 1

4. Квадрат с длиной стороны 24 см изображён на чертеже в масштабе 1 : 8. Какова длина стороны квадрата на чертеже?

1) 8 см
2) 2,4 см
3) 3 см
4) 6 см

5. Длина тела жука 8 мм. Этот жук изображён в книге в масштабе 4 : 1. Какова длина тела жука на рисунке в книге?

1) 3,2 см
2) 2 см
3) 32 см
4) 3,2 мм

6. Расстояние между двумя посёлками изображено на плане отрезком длиной 3 см. Масштаб плана 1 : 5000. Каково расстояние между посёлками в действительности?

1) 15 см
2) 150 см
3) 1500 м
4) 150 м

7. Высота вазы 0,4 м. Какую высоту будет иметь её изображение на рисунке, сделанном в масштабе 1 : 2?

1) 0,2 см
2) 20 см
3) 0,8 м
4) 2 см

8. На рисунке изображён отрезок АВ в масштабе 1 : 1. Какой длины будет отрезок АВ, если его изобразить в масштабе 1 : 3?

1) 0,3 см
2) 2,7 см
3) 3 см
4) 4 см

2 вариант

1. Как правильно записать масштаб карты, если один сантиметр на карте соответствует ста тысячам сантиметров на местности?

1) 10 000 : 1
2) 1 : 10 000
3) 1 : 1 000 000
4) 1: 100 000

2. Расстояние, равное 100 м, изображено на плане отрез­ком длиной 2 см. Определите масштаб плана.

1) 2 : 100
2) 1 : 5000
3) 1 : 50
4) 1 : 500

3. На одном чертеже гайка изображена в масштабе 10 : 1, а на другом та же гайка в масштабе 1 : 10. На каком чертеже изображение гайки увеличено в 10 раз по сравyению с её действительными размерами?

1) на первом в масштабе 10 : 1
2) на втором в масштабе 1 : 10

4. Равносторонний треугольник с длиной стороны 36 см, изображён на чертеже в масштабе 1 : 4. Какова длина, стороны треугольника на чертеже?

1) 4 см
2) 0,9 см
3) 9 см
4) б см

5. Длина ключа 30 мм. Этот ключ изображён на рисунке в масштабе 2 : 1. Какова длина ключа на рисунке?

1) 15 см
2) 6 мм
3) 1,5 см
4) 6 см

6. Расстояние между двумя деревнями изображено на плане отрезком длиной 5 см. Масштаб плана 1 : 2500. Каково расстояние между деревнями в действительности?

1) 125 км
2) 12,5 км
3) 500 м
4) 75 км

7. Высота стакана 10 см. Какую высоту будет иметь стакан, если его изобразить на рисунке в масштабе 1 : 2?

1) 5 см
2) 0,5 см
3) 2 см
4) 5 мм

8. На рисунке изображён отрезок АВ в масштабе 1 : 1. Какую длину будет иметь отрезок АВ, если его изобразить в масштабе 1 : 5?

1) 5 см
2) 0,5 см
3) 0,2 см
4) 2 см

Ответы на тест по математике Масштаб
1 вариант
1-3
2-4
3-2
4-3
5-1
6-4
7-2
8-3
2 вариант
1-4
2-2
3-1
4-3
5-4
6-2
7-1
8-4

PDF-версия
Тест Масштаб
(87 Кб, pdf)

Центральные ресурсы i-Ready | Семейный центр – часто задаваемые вопросы

Диагностика охватывает следующие Чтение области:

Фонологическая осведомленность – это понимание того, что произносимое слово состоит из разных частей и что каждая из этих частей производит звук. Например, слово летучая мышь включает в себя звуки /б/, /а/ и /т/, а слово тесто можно разбить на два слога, образующих звуки /летучая мышь/ и /тер/. Фонологическая осведомленность является важным строительным блоком для фонетики. Читатели должны быть в состоянии различать или различать отдельные звуки в произносимых словах, прежде чем они смогут полностью освоить сопоставление звуков с буквами.

Обучение Phonics учит учащихся связывать звуки, которые они слышат в произнесенных словах, с буквами, которые они видят в написанных словах. Например, учащийся, который может связать звуки с буквами, знает, что нужно читать «й» в , а затем как один звук /й/, а не звук /т/ и звук /ч/. Студенты должны изучить множество различных связей между звуками и образцами правописания. На самом деле существует так много связей, что изучение фонетики может показаться изучением правил для понимания скрытого кода. Но этот навык осваивается, делая один шаг за раз, изучая одно правило, затем другое и так далее. Как только учащиеся смогут быстро и легко установить эти связи, они действительно смогут начать читать со смыслом.

Высокочастотные слова — это слова, которые чаще всего встречаются в том, что читают учащиеся. Такие слова, как и , и , а также и , являются высокочастотными словами. Поскольку эти слова появляются так часто, читатели должны научиться распознавать их автоматически. Кроме того, эти слова часто пишутся так, что это может сбить с толку. Такие слова, как и там , не подчиняются правилам, связывающим звуки с буквами в большинстве слов. Обучение распознаванию этих слов автоматически помогает учащимся читать быстрее и легче, что дает им больше возможностей понять то, что они читают.

Словарь — это названия слов, которые знает учащийся. Чем больше слов знает учащийся, тем легче ему понять прочитанное. Хорошие читатели знают значения многих слов. Студенты расширяют свой словарный запас, слушая и читая новые слова, говоря о словах и изучая определенные слова.

Понимание: Литература описывает способность учащегося понимать типы письма, которые обычно выдуманы или вымышлены. Рассказы — это литературные тексты, которые учащиеся читают чаще всего, но пьесы и стихи также являются примерами литературных текстов. Учащийся, разбирающийся в литературе, может определить последовательность событий в рассказе, обсудить значение стихотворения или объяснить реплики, которые произносит персонаж в пьесе. По мере того, как ученик развивается как читатель, он может понимать рассказы, пьесы и стихи, которые становятся все более сложными.

Понимание: Информационный текст описывает способность учащегося понимать тип письма, который обычно соответствует действительности. Книги о науке или истории являются примерами информационного текста, как и статьи в газетах или журналах. Этот вид письма часто структурирован иначе, чем художественные тексты. Информационный текст часто не рассказывает историю и обычно состоит из разделов с заголовками. Кроме того, он может содержать диаграммы, диаграммы и графики, важные для понимания. Учащийся, который понимает информационный текст, может определить основную идею и вспомогательные детали, описать способ организации письма или извлечь информацию из фотографии или схемы.

Диагностика охватывает следующие области математики :

Числа и операции в классах K–8 относится к математическим навыкам, которые часто называют арифметическими, от чтения и записи чисел до сложения, вычитания, умножения и деления различных типов. чисел. Сюда входят целые числа, десятичные дроби, дроби, целые числа и иррациональные числа.

Алгебра и алгебраическое мышление  в классах K–8 относится к математическим навыкам, связанным с распознаванием числовых закономерностей, пониманием значения сложения, вычитания, умножения и деления, а также с использованием символов для написания и решения уравнений, включая те, которые используются для решения слов. проблемы. В старших классах эта область охватывает темы алгебры, связанные с использованием функций, уравнений и неравенств для моделирования математических ситуаций и решения задач путем количественных рассуждений и расширения понимания операций за пределы реальной системы счисления.

Измерение и данные в классах K–8 представляет собой широкий спектр математических навыков, связанных со сбором, организацией и интерпретацией числовой информации, от определения времени или использования линейки для измерения длины объекта до использования формул для нахождения объема. или площадь поверхности. Он также включает в себя понимание таблиц и графиков, а в более поздних классах — статистику и вероятность.

Геометрия в классах K–8 относится к различным навыкам, связанным с анализом двух- и трехмерных форм. К ним относятся называние и классификация фигур с использованием таких характеристик, как симметрия, количество сторон и угловая мера, а в более поздних классах — с использованием конгруэнтности и подобия. В старших классах эта область охватывает темы геометрии и измерений, связанные с развитием пространственных геометрических рассуждений, соединением геометрических свойств и уравнений, написанием доказательств и использованием понятий статистики и вероятности для анализа данных.

Эти сводки доменов, найденных в i‑Ready Diagnostic , можно загрузить и поделиться с помощью этого ресурса в формате PDF.

Образцы работ учащихся со шкалами Марцано

Вы работаете с выставлением оценок на основе стандартов, шкалами успеваемости или установкой на рост? Пытаетесь понять, как их оценивать? На этой странице представлены различные образцы работ учащихся со шкалами Марцано из моих оценок по математике для 4-го, 5-го и 6-го классов. Эти оценки были специально разработаны для документирования мастерства учащихся на каждом уровне. Студенты получают четкую визуальную обратную связь о своей работе, а вы получаете документацию, информацию о планировании, план для дифференциации и удобную страницу из двух замшевых материалов, которая работает как предварительный тест и посттест.

Оценка может быть сложной! Вначале я тратил много времени на просмотр и размышление над работами моих учеников. Я пересмотрел свои шкалы и оценки на основе отзывов, которые я получил от них. Ниже вы найдете несколько примеров оценок для 4-6 классов. Образцы могут не отражать всю шкалу для каждого стандарта, но часто показывают несколько уровней, чтобы получить хорошее представление о том, как учащиеся реагируют.

После каждого уровня обучения будут ссылки для поиска бесплатных образцов материалов. Попробуйте их в своем собственном классе. После некоторой практики становится легче решить, какой уровень мастерства у студентов. Надеюсь, вы найдете эти ресурсы, которые сделают ваше обучение гладким и эффективным!

С 1 по 8 классы можно ознакомиться на сайте Teacherspayteachers.com. Посетите вкладку МОЙ МАГАЗИН выше, найдите свой уровень в разделе «Категории».

На каждой странице продукта в моем магазине есть

комментариев учителей и отзывы, чтобы вы могли видеть, как они работают в других классах. 🙂

4.OA.3.1

В приведенном ниже примере работы этот учащийся определенно демонстрирует понимание задачи и процесса поиска нескольких возможностей с использованием списка. Его единственная ошибка в Шкала 1 b) заключалась в том, что он не осознавал, что в этой ситуации не следует учитывать повторяющиеся возможности. Например, ваниль и мята или мята и ваниль считаются одной возможностью; порядок не имеет значения. Чтобы помочь этому ученику исправить свои ошибки, мне
нужно сосредоточить его внимание на том, чтобы задать вопрос: «Нужно ли мне считать повторения?» Этот стандарт позволяет детям замечать разницу между комбинациями и перестановками в стандартах
средней школы.

В Масштаб 2 , у нас та же ситуация, когда повторы не учитываются. Таблица предназначена для того, чтобы учащиеся могли показать еще один точный способ отслеживания возможностей без использования древовидной диаграммы. Если учащийся попытается вместо этого использовать древовидную диаграмму, он получит 4 x 3 = 12 (если он не будет считать двойные порции одного и того же вкуса) или 4 x 4 = 16 (если он подсчитает двойные порции одного и того же вкуса). ). Этот учащийся точно насчитал 10 возможностей, используя таблицу, чтобы показать комбинации без повторений.

4.NBT.3

Масштабная оценка для этого стандарта настроена, чтобы показать последовательность подходов к
сравнения чисел. Шкала 1 предлагает учащимся сравнить числа с произвольными числами над и под собой.

Шкала 2 специально предлагает учащимся округлить до ближайших 10 или 100 выше и ниже числа.

Шкала 3 нацелена на ожидание уровня класса, что учащиеся смогут применить эту идею для округления.

В шкале 4 учащимся предлагается применить округление до десятичных знаков. Это выше уровня
класса и не ожидается в 4-м классе. У этого конкретного ученика не было проблем с округлением целых чисел, но он не устанавливал связь с десятичными знаками. На следующем уровне обучения с ним я планирую задать ему вопросы, которые помогут определить закономерность в процессе округления любого разрядного значения, а затем спросить его, как бы он применил тот же процесс к десятичным разрядам. В зависимости от его уровня концептуального понимания значений десятичных разрядов мне, возможно, придется использовать наглядные пособия, такие как десятичные квадраты, чтобы помочь ему увидеть, как десятые, сотые и тысячные доли будут выглядеть раскрашенными. Затем мы можем пройти тот же процесс округления до ближайший десятый, сотый и т. д.

4.NBT.5

В этом стандарте учащихся просят умножать многозначные числа. В Scale 3 этот учащийся демонстрирует мастерство самого умножения, но стандарт также требует, чтобы учащиеся «иллюстрировали и объясняли расчеты…». В Scale 4 он применяет те же стратегии, но только точно определяет «десятичные блоки». Мой следующий шаг — попросить его устно объяснить, какие стратегии он использовал и почему. Отсюда я могу

решить, следует ли переучить его конкретным названиям стратегий или не беспокоиться об этом.

Чтобы получить БЕСПЛАТНУЮ копию стандартов геометрии для 4-го класса (4. G.1-3),
, посетите магазин Mrs. L’s Leveled Learning на веб-сайте TeacherpayTeacher.com.

Чтобы получить копию полного оценивания, включая все общие базовые стандарты для 4-го класса по математике, нажмите ЗДЕСЬ. Вы также можете скачать БЕСПЛАТНУЮ ПРЕДВАРИТЕЛЬНУЮ ПРОСМОТР с этой страницы.

4 -й класс Математика с математикой Marzano: портфель прогресса студентов

4 -й класс для учителей математики

5.OA.2

. & 2  настоящего стандарта; умение переводить слова в выражения.

Однако в Шкалах 3 и 4 она делает ошибки, интерпретируя порядок операций для каждой ситуации. В задаче 3к) она поменяла местами х 4 и + 2, что дало бы неверный ответ. 3l) помечен как неверный, потому что она неправильно описала левую и правую задачи, которые объясняла, но я все же могу сказать, что она заметила разницу, не вычисляя задачу. В шкале 4 у нее было больше проблем с точным описанием ситуации. Я подчеркнул «проблема со словом» в указаниях, потому что она сдавала оценку только в письменном виде. Это была ее вторая попытка, и из нее я вижу, что она все еще пытается сопоставить описание с порядком операций в выражении. Она использует слово «удвоение», когда имеет в виду x 4. Для этой ученицы я решил дать ей пропуск только по шкалам 1 и 2, пока я не переучил и не дал ей больше возможностей для практики для правильного перевода порядка операций.

5.NBT.2

В шкалах 1 и 2  для этого стандарта учащимся предлагается повторить умножение на группы по 10 или 100. В шкалах 3 и 4 учащимся предлагается применить свои знания о показателях степени делать то же самое.

Эта ученица демонстрирует мастерство в стандарте для своего класса, потому что она сдала Шкала 3  с некоторыми краткими, но разумными объяснениями. Шкала 4  включает в себя более сложные задачи, с которыми она не справится как 5 ^-й -классник, но могла бы достичь, если бы заметила, что следует тому же процессу умножения и деления степеней десяти. Эта дивизия особенно сбила ее с толку. Она забыла, как двигать десятичную дробь, чтобы указать, сколько раз она поделила на десять.

В опубликованной копии этой оценки, 5 ^th  Оценка по общей основной математике с шкалами Марцано , я изменил  Шкала 4  , чтобы последние три задачи на деление давали одно и то же частное, даже если они имеют различные показатели десяти.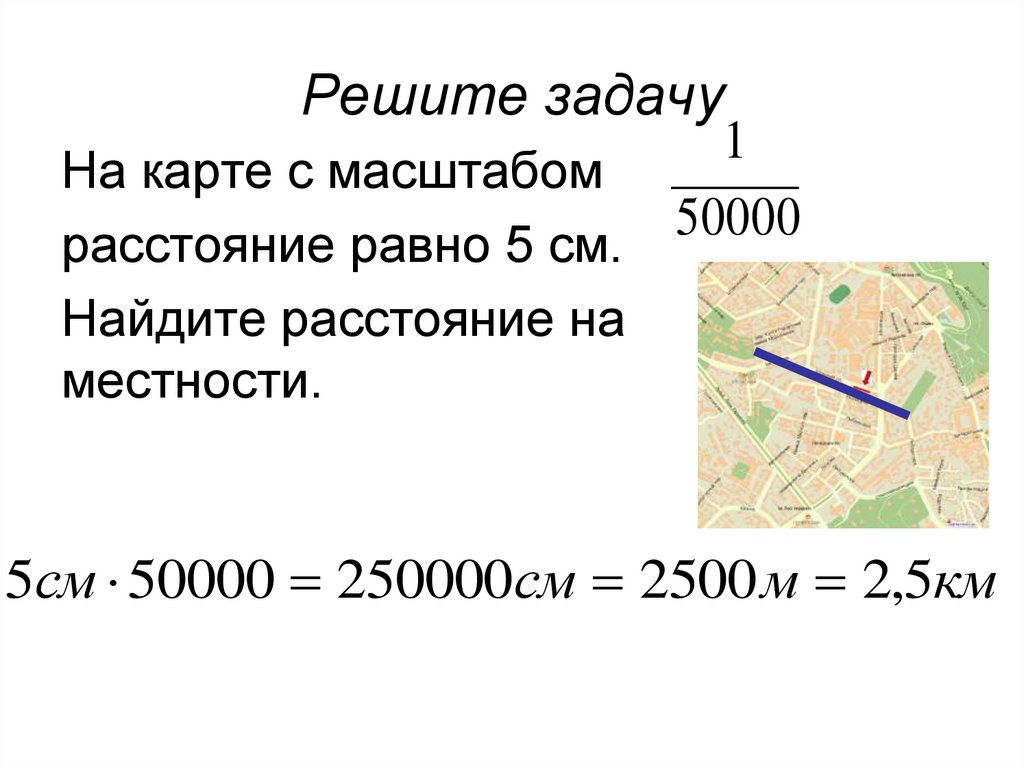 Я также изменила вопрос, чтобы дети должны были замечать и объяснять, почему они каждый раз получают одно и то же частное.

Я создал игру для SMARTboard в файле .notebook, чтобы помочь учащимся понять движение десятичного знака при умножении и делении чисел в степени десяти. На самом деле игра просит учеников переместить цифры своего числа на диаграмме разрядности, чтобы они установили связь, что на самом деле в разные места перемещаются цифры, а не десятичная дробь. На уроке я указываю на эти связи и проверяю, могут ли они начать применять их к большим числам, например, в шкале 4. Игра называется «9».0177 Place Value Volley , и у него есть несколько разных уровней, использующих разные обозначения для кратных десяти, показателей степени и преобразования метрической системы, потому что они работают одинаково.

5.NBT.1

Иногда ученик не «сдает» все шкалы, но все равно получает от меня пятерку . В приведенном ниже примере работа в Масштаб 1 не завершена, потому что десять и сто представлены неточно. Я отметил это студенту, но поскольку у него не было проблем с правильным выполнением шкал 2-4, я знаю, что он освоил этот стандарт, и мы пошли дальше.

Чтобы получить БЕСПЛАТНУЮ копию стандарта операций и алгебраического мышления для 5-го класса (5.OA.1-3),
, веб-сайт , посетите магазин Mrs. L’s Leveled Learning в магазине Teacher.com.

Чтобы получить копию полного оценивания, включая все общие базовые стандарты для 5-го класса по математике, нажмите ЗДЕСЬ. Вы также можете скачать БЕСПЛАТНУЮ ПРЕДВАРИТЕЛЬНУЮ ПРОСМОТР с этой страницы.

  *Примечание: Пересмотренная и опубликованная версия Оценок по математике для 5-го класса с шкалами Марцано  включает столбец ответов слева от каждого рабочего места для быстрой проверки нескольких учащихся одним взглядом. Ключ ответа   также указан в конце документа.

Математика 5-го класса со шкалами Марцано: Портфолио достижений учащихся

Контрольные листы для учителей математики 5-го класса

6.RP.3

Поднавыки a. и б. основываться на навыках 5-го класса (см. 5.OA.3) построения координат x и y с использованием таблицы значений, основанных на отношениях. В Шкала 2 я прошу студентов «иметь значение «y» для каждого значения «x» в сетке». его студент упустил из виду это направление и нанес на график только значения x и y из приведенной выше таблицы. Да, он правильно нанес точки, поэтому я могу с уверенностью сказать, что он прошел шкалу 2, но в этой ситуации я попрошу его добавить недостающие значения, чтобы я мог видеть, как он применяет правильное соотношение к новым значениям x.

Дополнительные навыки c. и д. рассматриваются в по шкалам 3 и 4 данной оценки. В задаче 3d) ученик правильно рассчитал дополнительное время в 176 миль. Вы могли заметить, что опубликованная версия была изменена, и теперь учащиеся решают в общей сложности 176 миль вместо 165 + 176 миль. Задача 3e) была рассчитана неправильно, потому что его работа показывает, что он пытался выяснить, сколько раз 15 переходит в 100%, но это не работает равномерно, поэтому его стратегия приблизила его, но не к точному ответу в 25 долларов. Моя стратегия работы с этим студентом состоит в том, чтобы пересмотреть стратегии проверки его работы с процентами; работая в обратном порядке или используя эквивалентные дроби, чтобы проверить, соответствует ли отношение части процентов к целому его решению. Например, если бы он сравнил 15/100 с 3,75/24 доллара, то увидел бы, что 3,75 х 4 составляет 15, а 24 х 4 не дает 100! Так как это единственная задача, которая была некорректна в Шкала 3 , и он дал достойный ответ для Шкала 4 , я уверен, что он освоил этот стандарт, но все еще нуждается в некоторой доработке, чтобы проверить его работу.

6.NS.1

Чтобы создать шкалу 1 и 2 для этого стандарта, я привел 4.NBT.6 и 5.NF.7 в качестве предыдущих стандартов, которые учащиеся могут использовать для деления дробей. Первая идея заключается в том, что умножение и деление являются обратными операциями, которые можно использовать для проверки друг друга. Это полезно, когда учащиеся только начинают понимать деление и дроби, и у них может возникнуть соблазн угадать ответы, потому что они не могут визуализировать то, что происходит. Шкала 2 напоминает учащимся, что нужно задуматься о значении умножения и деления дробей на целые числа. В инструкциях учащимся специально предлагается «нарисовать картинку» каждой проблемы, потому что в стандарте также делается упор на использование визуальных моделей. Эта ученица попыталась вместо этого преобразовать дроби в десятичные и не смогла увидеть, что делает ошибки. Если бы она нарисовала изображение 1/4 целого, а затем разделила его на 5 равных частей, то легко поняла бы, что 20 частей поместятся в 1 целое = 1/20.

Когда я перешел с преподавания в 1-м классе на 3-4-5-6 классы по математике, мне пришлось потратить немного времени на самостоятельное деление дробей. Рисование моделей помогло мне понять, как дробь может быть разбита на другую дробь. Визуальный аспект здесь имеет важное значение! Тем более, что Шкала 3 , которая является целью этого стандарта, просит учащихся представить деление дробей на дроби, что еще сложнее, чем целые числа. Здесь она попыталась просто разделить на 2, а затем на 5, что могло бы сработать, если бы она точно разделила 16 унций. на 10 равных частей и создал упрощенную фракцию. Например, если 16 унций. деленное на 10 равно 1,6 унции, тогда 1,6/16 = 1/10.

6.NS.4

Здесь учащихся просят использовать навыки, которые они получили с 5-го класса (множители, множители и свойство распределения) особым образом. Этот ученик, несомненно, демонстрирует мастерство в этом стандарте. Я выбрал это как пример хорошего объяснения вопроса 3p).

6.NS.6

В ключах ответов, включенных в опубликованные версии оценки, не так много изображений, поэтому вот краткое изображение точной сетки. Это помогает мне быстрее оценивать, если мне не нужно перечитывать координаты для каждой точки. Вы заметите, что Scale 4 не включен в этот стандарт, потому что в Scale 3 так много всего нужно вписать. Я думал, что рабочее пространство важнее, чем изобретение расширения.

6.NS.7

В 6.NS.6 учащимся предлагается применить понимание отрицательных целых чисел к координатным сеткам. В 6.NS.7 они должны применять его к новым контекстам, таким как сюжетные задачи. Учащиеся должны быть в состоянии определить контекст для положительных, отрицательных и абсолютных значений, но еще не обязаны решать операции. Вот почему Шкала 4 показывает задачи выше уровня класса: вычисления с целыми числами. Этот ученик демонстрирует мастерство стандарта и способность применять это понимание к сложению и вычитанию целых чисел. Диаграммы уровня моря помогают им визуализировать положение целых чисел, как это сделала бы числовая линия. Дополнением к этим заданиям может быть просьба к учащимся нарисовать свою собственную диаграмму на основе сюжетной задачи, а затем проверить, правильно ли они интерпретировали положение чисел.

Чтобы получить БЕСПЛАТНУЮ копию Стандартов соотношения и пропорциональных отношений для 6-го класса (6.RP.1-3),
, посетите магазин Mrs. L’s Leveled Learning на веб-сайте TeacherpayTeacher.com.

Чтобы получить копию полного оценивания, включая все общие базовые стандарты для 6-го класса по математике, нажмите ЗДЕСЬ. Вы также можете скачать БЕСПЛАТНУЮ ПРЕДВАРИТЕЛЬНУЮ ПРОСМОТР с этой страницы.

*Примечание: Пересмотренная и опубликованная версия Оценивание по математике для 6-го класса с использованием шкал Марцано  включите столбец ответов слева от каждого рабочего места, чтобы быстро проверить нескольких учащихся одним взглядом.