Содержание
Тест по математике Масштаб (6 класс)
Последний раз тест пройден 4 часа назад.
Для учителя
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Как правильно записать масштаб карты, если один сантиметр на карте соответствует двум миллионам сантиметров на местности?
1 : 200 000
2 000 000 : 1
1 : 2 000 000
1 : 2000
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 2 из 10
Расстояние, равное 60 м, изображено на плане отрезком, длиной 4 см.
 Определите масштаб плана.
Определите масштаб плана.4 : 60
1 : 15
4 : 6000
1 : 1500
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 3 из 10
На одном чертеже деталь изображена в масштабе 1 : 5, а на другом — та же деталь в масштабе 5 : 1. На каком чертеже изображение детали получилось увеличенным в 5 раз по сравнению с действительными размерами детали?
На первом в масштабе 1 : 5
На втором в масштабе 5 : 1
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 4 из 10
Квадрат с длиной стороны 24 см изображён на чертеже в масштабе 1 : 8. Какова длина стороны квадрата на чертеже?
192 см
2,4 см
3 см
6 см
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 5 из 10
Длина тела жука 8 мм.
 Этот жук изображён в книге в масштабе 4 : 1. Какова длина тела жука на рисунке в книге?
Этот жук изображён в книге в масштабе 4 : 1. Какова длина тела жука на рисунке в книге?3,2 см
2 см
32 см
3,2 мм
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 6 из 10
Расстояние между двумя посёлками изображено на плане отрезком длиной 3 см. Масштаб плана 1 : 5000. Каково расстояние между посёлками в действительности?
15 см
150 см
1500 м
150 м
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 7 из 10
Высота вазы 0,4 м. Какую высоту будет иметь её изображение на рисунке, сделанном в масштабе 1 : 2?
0,2 см
20 см
0,8 м
2 см
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 8 из 10
Равносторонний треугольник с длиной стороны 36 см, изображён на чертеже в масштабе 1 : 4.
 Какова длина, стороны треугольника на чертеже?
Какова длина, стороны треугольника на чертеже?144 см
0,9 см
9 см
б см
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 9 из 10
Высота стакана 10 см. Какую высоту будет иметь стакан, если его изобразить на рисунке в масштабе 1 : 2?
5 см
0,5 см
20 см
5 мм
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Вопрос 10 из 10
Расстояние, равное 100 м, изображено на плане отрезком длиной 2 см. Определите масштаб плана
2 : 100
1 : 5000
1 : 50
1 : 500
Подсказка
Правильный ответ
Неправильный ответ
В вопросе ошибка?
Доска почёта
Чтобы попасть сюда — пройдите тест.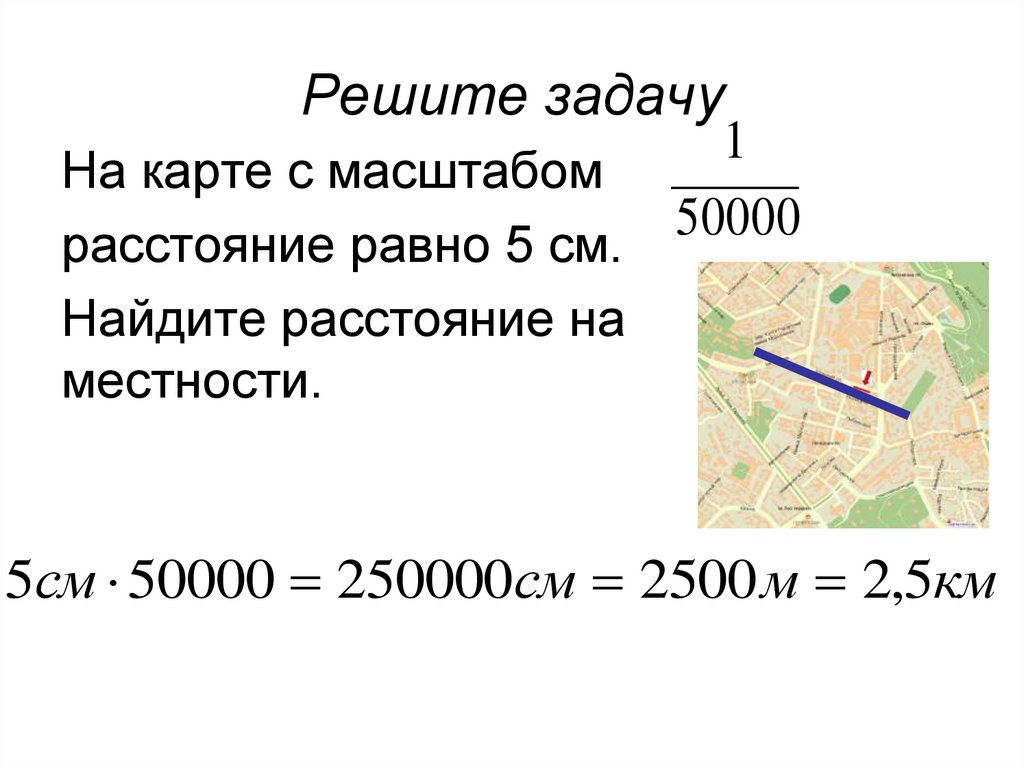
Тест «Масштаб» (6 класс) рассчитан на учеников средней школы. Ответы к заданиям уже даны, поэтому с помощью теста можно быстро оценить себя и более качественно подготовиться к занятию по теме. Вопросы проверяют умение расшифровывать масштабы и преобразовывать их.
Тест по математике «Масштаб» целесообразно использовать в процессе подготовки к тематической контрольной работе, итоговой проверке.
Рейтинг теста
4
Средняя оценка: 4
Всего получено оценок: 525.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Как найти Масштаб в Математике?
Понятие масштаба
Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.
Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.
Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.
- Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Масштаб бывает трех видов:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
- линейный, зная величину масштаба, можно определить расстояния.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Определение масштаба на карте
На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.
Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.
Масштаб — это отношение размера изображения к размеру изображаемого объекта.
Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.
На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.
Численные масштабы карт и соответствующие им масштабы на местности:
Масштаб 1 : 100 000
- 1 мм на карте — 100 м (0,1 км) на местности
- 1 см на карте — 1000 м (1 км) на местности
- 10 см на карте — 10000 м (10 км) на местности
Масштаб 1 : 10000
- 1 мм на карте — 10 м (0,01 км) на местности
- 1 см на карте — 100 м (0,1 км) на местности
- 10 см на карте — 1000 м (1 км) на местности
Масштаб 1 : 5000
- 1 мм на карте — 5 м (0,005 км) на местности
- 1 см на карте — 50 м (0,05 км) на местности
- 10 см на карте — 500 м (0,5 км) на местности
Масштаб 1 : 2000
- 1 мм на карте — 2 м (0,002 км) на местности
- 1 см на карте — 20 м (0,02 км) на местности
- 10 см на карте — 200 м (0,2 км) на местности
Масштаб 1 : 1000
- 1 мм на карте — 100 см (1 м) на местности
- 1 см на карте — 1000 см (10 м) на местности
- 10 см на карте — 100 м на местности
Масштаб 1 : 500
- 1 мм на карте — 50 см (0,5 метра) на местности
- 1 см на карте — 5 м на местности
- 10 см на карте — 50 м на местности
Масштаб 1 : 200
- 1 мм на карте — 0,2 м (20 см) на местности
- 1 см на карте — 2 м (200 см) на местности
- 10 см на карте — 20 м (0,2 км) на местности
Масштаб 1 : 100
- 1 мм на карте — 0,1 м (10 см) на местности
- 1 см на карте — 1 м (100 см) на местности
- 10 см на карте — 10м (0,01 км) на местности
Решение задач на масштаб
Для закрепления темы решим несколько математических задач на масштаб за 6 класс.
Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.
Как решаем:
8 см — это 1 часть
8 * 10 000 = 80 000 (см) — это 10 000 частей
80 000 см = 800 м
Ответ: 800 м
Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.
Как решаем:
400 км = 400 000 м = 40 000 000 см
40000000 : 5000000 = 40 : 5 = 8
Ответ: 8 см
Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?
Как решаем:
700 км = 700 000 м = 70 000 000 см
70 000 000 : 14 = 5 000 000
Ответ: уменьшить в 5 000 000 раз.
Вы здесь: Главная → Рабочие листы → 6 класс Это обширная коллекция бесплатных печатных листов по математике для шестого класса, упорядоченных по таким темам, как умножение, деление, показатель степени, разрядное значение, алгебраическое мышление, десятичные дроби, единицы измерения, отношение, проценты, разложение на простые множители, GCF, LCM, дроби, целые числа и геометрия. Они генерируются случайным образом, могут быть распечатаны из вашего браузера и содержат ключ ответа. Рабочие листы поддерживают любую математическую программу для шестого класса, но особенно хорошо подходят для математической программы IXL для 6-го класса. Прыжки до: GEOMETRY GEOMERSTER . Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на приведенные ниже ссылки. Вы также можете получить новый, другой, просто обновив страницу в браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не помещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре. В некоторых браузерах и принтерах есть опция «Печать по размеру», которая автоматически масштабирует рабочий лист в соответствии с областью печати. Все рабочие листы поставляются с ключом ответа, размещенным на 2-й странице файла. В шестом классе учащиеся начнут изучение начальной алгебры (порядок операций, выражений и уравнений). Они узнают о соотношениях и процентах и начинают использовать целые числа. Учащиеся также повторяют деление в столбиках, разложение на множители, дробную арифметику и десятичную арифметику. Умножение и деление и некоторый обзорДлинное умножение
. . Полное деление
Преобразование единиц измерения с использованием деления и умножения в длинном столбце
Математика для начальных классов Эдварда Заккаро Хорошая книга по решению задач с очень разнообразными текстовыми задачами и стратегиями решения задач. Экспоненты
Разрядное значение/Округление
АлгебраПорядок операций
Выражения
Уравнения
Key to Algebra Workbooks Key to Algebra предлагает уникальный проверенный способ познакомить учащихся с алгеброй. => Узнать больше Дроби и десятичные дроби
Десятичное сложение и вычитание
Рабочие тетради Key to Decimals Это серия рабочих тетрадей от Key Curriculum Press, которая начинается с основных понятий и операций с десятичными знаками. В комплект входят книги 1-4. => Узнать больше Десятичное умножениеУмножение в уме
Умножить в столбцах
Десятичное делениеПсихическое отделение
Полное деление
Измерительные блокиТрадиционная система Преобразование единиц измерения с помощью деления и умножения (бумага и карандаш) или математических вычислений в уме
Преобразование с помощью калькулятора с десятичными дробями
Метрическая система
Соотношение
Процент
. Факторизация простых чисел, GCF и LCM
Сложение и вычитание дробей
Умножение дробей Во всех задачах на умножение и деление дробей полезно упростить перед умножением.
Дробное деление
Преобразование дробей в смешанные числа и vv
Упрощенные или эквивалентные дроби
Дроби и десятичные дроби
Целые числаКоординатная сетка
Сложение и вычитание Сложение и вычитание целых чисел не входят в Общие базовые стандарты для 6-го класса, но некоторые учебные программы или стандарты могут включать их в 6-й класс.
Умножение и деление Умножение и деление целых чисел не входят в Общие базовые стандарты для 6-го класса, но ссылки на рабочие листы включены сюда для полноты картины, поскольку некоторые учебные программы или стандарты могут включать их в 6-й класс.
ГеометрияПлощадь — эти листы выполняются в координатной сетке.
Объем и площадь поверхности Поскольку эти листы ниже содержат изображения разных размеров, сначала проверьте
. Пропорции
Круг
Если вы хотите лучше контролировать такие параметры, как количество задач, размер шрифта, расстояние между задачами или диапазон чисел, просто Меню математических листов 1 -й класс Рабочие листы Римские цифры Классификация треугольников Австралийские деньги 6 Деньги Британские деньги Рабочие листы дробей 1 Десятичные рабочие листы процент/десятичный Калькулятор уравнений |
Уроки формирующего оценивания
Classroom Challenges — это уроки, которые помогают учителям в формирующем оценивании. Всего 100 уроков, по 20 в каждом классе с 6 по 8 и 40 на тему «Готовность к карьере и колледжу» в 9 классе средней школы.и выше. Одни уроки направлены на развитие математических понятий, другие на решение нестандартных задач.
Перед первым использованием этих уроков рекомендуется прочитать Краткое руководство для учителей и администраторов (PDF).
Каждый урок можно загрузить в виде универсального PDF-файла для распечатки, а также вспомогательную презентацию PowerPoint.
Поиск урока
Существует несколько способов навигации:
- Используйте меню слева, чтобы просмотреть оценки и темы или выполнить поиск по ключевой фразе.

 Определите масштаб плана.
Определите масштаб плана.
 В геометрии основное внимание уделяется площади треугольников и многоугольников и объему прямоугольных призм. Другие темы включают округление, показатели степени, GCF, LCM и единицы измерения. Обратите внимание, что эти бесплатные рабочие листы не охватывают все темы 6-го класса; в частности, они не включают решение проблем.
В геометрии основное внимание уделяется площади треугольников и многоугольников и объему прямоугольных призм. Другие темы включают округление, показатели степени, GCF, LCM и единицы измерения. Обратите внимание, что эти бесплатные рабочие листы не охватывают все темы 6-го класса; в частности, они не включают решение проблем. Включает в себя главы: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы каждой главы разбиты на четыре уровня: простые, несколько сложные, сложные и очень сложные.
Включает в себя главы: последовательности, решение проблем, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы каждой главы разбиты на четыре уровня: простые, несколько сложные, сложные и очень сложные. Новые концепции объясняются простым языком, а примеры легко понять. Словесные задачи связывают алгебру со знакомыми ситуациями, помогая учащимся понять абстрактные понятия. Учащиеся развивают понимание, решая уравнения и неравенства интуитивно, прежде чем вводятся формальные решения. Учащиеся начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 знакомят с рациональными числами и выражениями. Книги 8-10 расширяют охват вещественной системы счисления.
Новые концепции объясняются простым языком, а примеры легко понять. Словесные задачи связывают алгебру со знакомыми ситуациями, помогая учащимся понять абстрактные понятия. Учащиеся развивают понимание, решая уравнения и неравенства интуитивно, прежде чем вводятся формальные решения. Учащиеся начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 знакомят с рациональными числами и выражениями. Книги 8-10 расширяют охват вещественной системы счисления. Затем книги охватывают реальное использование десятичных знаков в ценообразовании, спорте, метриках, калькуляторах и науке.
Затем книги охватывают реальное использование десятичных знаков в ценообразовании, спорте, метриках, калькуляторах и науке. )
)



 если это не
если это не : сложение,
: сложение, 