Содержание
Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением
Занимательная
математика
Дошкольнику | 1 класс |
2 класс | 3 класс
| 4 класс
Упражнения на сложение и вычитание, умножение и деление, логические задачи можно
подать совершенно по-разному. Мы знаем, как увлечь ребёнка математикой!
Попробуйте развивающий курс ЛогикЛайк!
Выберите возраст для старта
Дошкольник
1 класс
2 класс
3 класс
Почему дети и родители выбирают ЛогикЛайк?
2 варианта занятий,
выбор сложности
-
Пройдите 3 стартовые главы курса логики
– и откройте доступ к разным категориям. Попробуйте
Попробуйте
«Закономерности», «Логические задачи», «Умный счёт» и другие. -
Попробуйте задания разного уровня сложности:
«Новичок», «Опытный», «Эксперт».
Начать занятия!
Начать занятия!
На LogicLike.com
дети учатся рассуждать, развивают логику, способности к математике
и познавательный интерес.
Занятия логикой и математикой онлайн
В 1-2 классе особенно важно заинтересовать детей решением задач.
Чтобы помочь родителям и учителям, команда опытных методистов и педагогов
«ЛогикЛайк» регулярно создает новые уроки, упражнения и тесты.
Наши арифметические, логические и другие задачи повышают интерес к математике
и успеваемость в школе.
У нас есть всё, что вы искали
Попробуйте полный курс ЛогикЛайк!
Математические задачи
и задания
Задачи на логику
Числовые и предметные
закономерности
Фигуры и развёртки,
геометрические задачи
Начать курс!
В разминке будут простые вопросы. Постепенно сложность нарастает, открываются новые
Постепенно сложность нарастает, открываются новые
интересные задания.
Популярные категории заданий
Подборки из обучающего курса
ЛогикЛайк
- Логические
задачи для 2 класса - Примеры для 2
класса - Математические ребусы для 2 класса
- Закономерности
для 2 класса - Составные
задачи в 2 действия для 2 класса - Задачи на умножение для 2 класса
Если вам нужно проверить, как ребёнок справляется со школьной программой, предложите
ему наши тесты для 2 класса
по математике.
Текстовые задачи
Вы можете начать занятия онлайн или просто посмотреть примеры заданий по математике
для 2 класса.
Задача 1.
Арифметика и логика
Для праздника Профессор купил голубые, красные и жёлтые воздушные шары.
Всего — 39 штук. Жёлтых и голубых вместе — 20.
Красных и голубых — 31.
Сколько красных шаров купил Профессор?
Показать
ответ
Ответ:
19.
Решение
Использовать все данные можно, но решение окажется
длинным, нерациональным.
На самом деле, достаточно от общего количества шаров
отнять количество жёлтых и голубых:
39 — 20 = 19.
Взять
подсказку
В задаче есть
небольшая «ловушка» — лишние данные.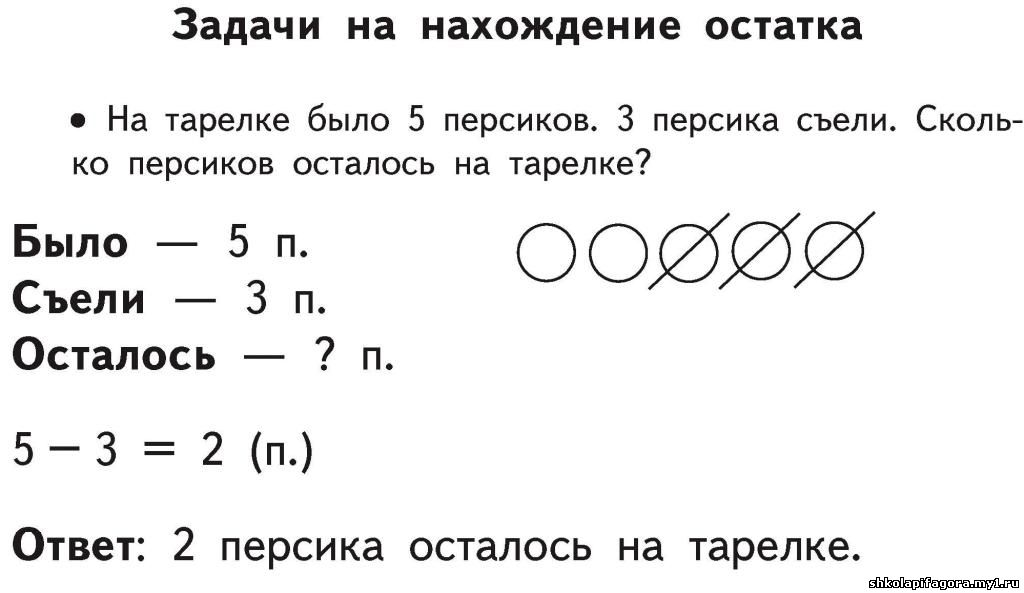
Задача 2. На сравнение
количества
На летних каникулах ребята делали фото насекомых. Витя сделал на 8 фото
больше, чем Ян, а Сергей на 5 фото больше, чем Витя.
НА сколько больше фото сделал Сергей, чем Ян?
Узнать ответ
Ответ:
13.
Задача 3.
 Составная на вычитание
Составная на вычитание
или деление
У Профессора на столе лежали упаковки батареек. В каждой по 12 штук. Когда
Профессор взял по 9 батареек из каждой упаковки, на столе осталось всего 15
батареек.
Сколько упаковок с батарейками было на столе?
Узнать ответ
Ответ:
5.
Решение
Когда Профессор взял из каждой упаковки по 9
батареек, осталось по 3 батарейки в каждой (12 — 9 =
3).
Вариант 1: Так как всего осталось 15 батареек, то
упаковок было 5 (15 — 3 — 3 — 3 — 3 — 3 =
0).
Вариант 2: Можно решать делением: 15 ÷ 3 = 5.
Посмотрите примеры олимпиадных заданий
для 2 класса или начинайте занятия.
Попробуйте полный курс занимательной математики
и логики от ЛогикЛайк
- Гибкий ум
и уверенность! Когда дети решают
задачи и головоломки на LogicLike, они тренируют «извилины»
и развивают смекалку.
- Фундамент
для IT! Алгоритмы,
закономерности, логика — всё это у нас есть. Мы учим работать с
информацией, тренируем память и мышление — формируем потенциал успеха в
IT-профессиях. - Повышаем
успеваемость! Регулярные
занятия по 20-30 минут развивают логические и математические
способности. Как следствие — высокие оценки в школе, призовые места
на олимпиадах и в конкурсах, повышается интерес к учёбе
вообще.
Начать занятия!
Примеры в картинках
Восстанови равенство
Чтобы решать
задачи, нажмите Начать занятия!
За звездочкой может быть спрятана любая цифра.
Восстанови пример, чтобы равенство стало верным.
Узнать ответ
Ответ:
58-27=31.
Решение
8-7=1
Какое число нужно отнять от 58, чтобы получить 31?
Число 27.
Взять
подсказку
От какого числа
надо отнять 7, чтобы получить 1?
Ребус в таблице
Чтобы решать
задачи, нажмите «Начать занятия»!
Одинаковые предметы имеют одинаковую цену.
Число обозначает общую стоимость предметов в столбце или в строке.
Догадайся, какое число нужно указать вместо знака вопроса.
Узнать ответ
Ответ:
180.
Решение
Кукуруза и тыква стоят столько же, сколько кукуруза
и три луковицы.
Cледовательно, 3 луковицы стоят столько же, сколько
1 тыква.
Представь теперь, что в таблице вместо 3 луковиц
нарисована 1 тыква и увидишь, что в нижней строке
тыква и перец вместе стоят 180, а во втором столбике
также стоит воображаемая тыква и тот же
перец.
Сколько они будут стоить вместе — и считать не
нужно.
Взять
подсказку
Посмотри
внимательно на картинку и определи, какие наборы овощей
стоят одинаково.
Можно посмотреть примеры других арифметических ребусов на сложение и
вычитание или приступить к занятиям на сайте.
Предложенные задания — часть образовательной платформы LogicLike.
Задачи на площадь и периметр
Задача 4. Ломаная линия
Чтобы решать
задачи, нажмите «Начать занятия»!
Отрезки одинакового цвета имеют одинаковую длину. Какая ломаная линия самая
длинная?
Узнать ответ
Ответ:
1.
Задача 5. Периметр
Чтобы решать
задачи, нажмите «Начать занятия»!
Профессор сделал 3 рамки из проволоки: треугольную, пятиугольную и
прямоугольную. И попросил робота Клапана выбрать самую длинную.
Помоги Клапану справиться с задачей.
Узнать ответ
Ответ:
прямоугольник
(10+2+10+2=24 см).
Задача 6. Площадь
Чтобы решать
задачи, нажмите «Начать занятия»!
Иришка вырезала два одинаковых (по площади) треугольника, два одинаковых
круга и два одинаковых четырёхугольника.
На какую фигуру Иришка израсходовала меньше всего бумаги?
Смотреть
ответ
Ответ:
Четырёхугольники
полностью помещаются и в круг, и в треугольник. Значит,
Значит,
площадь четырёхугольника самая маленькая.
Здесь лишь малая часть заданий, доступных ученикам образовательной
платформы ЛогикЛайк.
Какой формат занятий вы ищете?
Если ваша единственная цель — отработка навыков счета, найдите арифметический тренажер в
формате журнала или онлайн.
Для кого мы создали и постоянно развиваем сайт LogicLike?
- Для тех, кто хочет научиться думать, рассуждать, мыслить
нестандартно. - Для детей, чьи родители понимают что математика — это
не только примеры и задачи (подробнее — в статье о пользе от
занятий математикой).
- Для всех, кто хочет научиться принимать решения не только на
уроках математики, но и преуспевать в разных областях жизни.
Понравился материал? Поделитесь с друзьями!
Подключайтесь к ЛогикЛайк!
Более 150 000 ребят со всего мира уже
занимаются математикой и логикой с удовольствием
Начать обучение!
Начать обучение!
Мы научим ребёнка
Рассуждать и принимать решения
Решать любые логические задачи
Мыслить гибко
и нестандартно
Другие категории заданий
по возрасту
Математика для детей 5 — 6 лет
Задачи для 1 класса
Задачи для 3 класса
Задачи для 4 класса
10 увлекательных задач от советского математика
12 сентября 2021Отдых
Попробуйте решить головоломки от популяризатора математики Бориса Кордемского, не пользуясь подсказками.
Поделиться
0
1. Переправа через реку
Небольшой воинский отряд подошёл к реке, через которую необходимо было переправиться. Мост сломан, а река глубока. Как быть? Вдруг офицер замечает у берега двух мальчиков в лодке. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке. Каким образом?
Показать ответ
Скрыть ответ
2. Сколько деталей?
В токарном цехе завода вытачиваются детали из свинцовых заготовок. Из одной заготовки — деталь. Стружки, получившиеся при выделке шести деталей, можно переплавить и приготовить ещё одну заготовку. Сколько деталей можно сделать таким образом из тридцати шести свинцовых заготовок?
Показать ответ
Скрыть ответ
3. Во время прилива
Недалеко от берега стоит корабль со спущенной на воду верёвочной лестницей вдоль борта. У лестницы десять ступенек; расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды.
Самая нижняя ступенька касается поверхности воды.
Океан сегодня очень спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см. Через какое время покроется водой третья ступенька верёвочной лесенки?
Показать ответ
Скрыть ответ
4. Девяносто девять
Сколько нужно поставить знаков «плюс» (+) между цифрами числа 987 654 321, чтобы в сумме получилось 99?
Показать ответ
Скрыть ответ
5. Для Цимлянского гидроузла
В выполнении срочного заказа по изготовлению измерительных приборов для Цимлянского гидроузла приняла участие бригада в составе опытного бригадира и девяти молодых рабочих.
В течение дня каждый из юных рабочих смонтировал по 15 приборов, а бригадир — на 9 приборов больше, чем в среднем каждый из десяти членов бригады. Сколько всего измерительных приборов было смонтировано бригадой за один рабочий день?
Показать ответ
Скрыть ответ
6. Попробуйте отвесить
В пакете находится 9 кг крупы. Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Показать ответ
Скрыть ответ
7. Смышлёный малыш
Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:
— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.
Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну. Сколько же лет было малышу и каждому из остальных братьев?
Показать ответ
Скрыть ответ
8.
 Раздробить на части
Раздробить на части
Раздробите 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвёртую разделить на 2, то все результаты будут равными. Сумеете сделать?
Показать ответ
Скрыть ответ
9. Посадка деревьев
Пятиклассникам и шестиклассникам было поручено посадить деревья по обе стороны улицы по равному количеству на каждой стороне.
Чтобы не ударить лицом в грязь перед шестиклассниками, пятиклассники вышли на работу пораньше и успели посадить 5 деревьев, пока пришли старшие ребята, но оказалось, что они сажали деревья не на своей стороне.
Пришлось пятиклассникам идти на свою сторону и вновь начинать работу. Шестиклассники, конечно, справились с задачей раньше. Тогда учитель предложил:
— Пойдём, ребята, поможем пятиклассникам!
Все согласились. Перешли на другую сторону улицы, посадили 5 деревьев, отдали, значит, долг, да ещё успели посадить 5 деревьев, и вся работа была закончена.
— Хоть вы пришли раньше нас, а всё-таки мы вас обогнали, — посмеялся один шестиклассник, обращаясь к младшим ребятам.
— Подумаешь, обогнали! На 5 деревьев только, — возразил кто-то.
— Нет, не на 5, а на 10, — зашумели шестиклассники.
Спор разгорался. Одни настаивают на том, что на 5, другие пытаются как-то доказать, что на 10. Кто же прав?
Показать ответ
Скрыть ответ
10. Четыре теплохода
В порту пришвартовались 4 теплохода. В полдень 2 января они одновременно покинули порт. Известно, что первый теплоход возвращается в этот порт через каждые 4 недели, второй — через каждые 8 недель, третий — через 12 недель, а четвёртый — через 16 недель.
Когда в первый раз теплоходы снова сойдутся все вместе в этом порту?
Показать ответ
Скрыть ответ
Задачи для этой подборки взяты из сборника «Математическая смекалка» Бориса Кордемского, который выходил в издательстве «Альпина Паблишер».
Читайте также 🔥
- 15 занимательных задач для тренировки ума и сообразительности
- 11 хитрых советских головоломок для проверки логики и сообразительности
- 5 задач, которые предлагают решить на собеседованиях в Google и других компаниях
Решение неравенств с помощью пошагового решения математических задач
В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача
Эти методы включают переписывание задач в виде символов. Например, поставленная задача
«Найдите число, которое при прибавлении к 3 дает 7»
можно записать так:
3 + ? = 7, 3 + n = 7, 3 + x = 1
и т. д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:
3 + x = 7
будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определить, является ли значение 3 решением уравнения член.
4(3) — 2 = 3(3) + 1
12 — 2 = 9 + 1
10 = 10
Ответ. 3 это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.
Пример 2 Найдите решение каждого уравнения путем проверки.
а. х + 5 = 12
б. 4 · x = -20
Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.
Если к обоим элементам добавляется или вычитается одно и то же количество
уравнения, полученное уравнение эквивалентно исходному
уравнение.
В символах
a — b, a + c = b + c и a — c = b — c
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
x + 3 = 7
путем вычитания 3 из каждого члена.
Решение Вычитание 3 из каждого члена дает
x + 3 — 3 = 7 — 3
или
x = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же. для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.
Объединение одинаковых членов дает
x — 2 = 10
Добавление 2 к каждому члену дает
x-2+2 = 10+2
x = 12
Чтобы решить уравнение, мы используем сложение-вычитание свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим
2x + 1- 1 = x — 2- 1
2x = x — 3
Если теперь мы прибавим -x к каждому члену (или вычтем x из него), мы получим
2x-x = x — 3 — х
х = -3
где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнение
2(-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не заботясь о смене знака. Таким образом,
Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько различные способы применения указанного выше свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала прибавим -3x к каждому элементу, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
где переменная имеет отрицательный коэффициент. Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2х-2х + 9 = 3х- 9-2х+ 9
9 = х
откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА ДЕЛЕНИЯ
Рассмотрим уравнение
3x = 12
Решением этого уравнения является 4. Также обратите внимание, что если мы разделим каждую часть уравнения на 3, мы получим уравнения
Также обратите внимание, что если мы разделим каждую часть уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения разделить на одно и то же (отличное от нуля)
полученное уравнение эквивалентно исходному уравнению.
В символах
эквивалентны уравнениям.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Деление обоих членов на -4 дает
При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые члены, чтобы получить
5y = 20
Затем, разделив каждый член на 5, мы получаем
В следующем примере мы используем сложение — свойство вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее , объединение одинаковых членов дает
3x = -9
Наконец, мы делим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения умножая каждый член уравнения на 4, мы получаем уравнения
, решение которых также равно 12. В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
В символах
a = b и a·c = b·c (c ≠ 0)
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
, умножив каждый член на 6.
Решение Умножив каждый член на 6, получим
дроби.
Пример 2 Решить
Решение Сначала умножьте каждый член на 5, чтобы получить
Теперь разделите каждый член на 3,
Пример 3 Решите .
Решение Сначала упростим над дробной чертой, чтобы получить
Затем умножим каждый член на 3, чтобы получить
Наконец, разделив каждый член на 5, получим
ДОПОЛНИТЕЛЬНЫЕ РЕШЕНИЯ 90 все методы, необходимые для решения большинства уравнений первой степени. Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.
Шаги для решения уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство Division, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем +2x и +7 к каждому элементу и объединяем одинаковые члены, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы делим каждый член на 7, чтобы получить
В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Сначала мы объединяем одинаковые члены, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы делим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.
Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть
d = rt
(24) = (3)t
8 = t
Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие. Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить
, из которых по закону симметрии
В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить
затем разделив каждый член на a, мы получим
Фактор полинома или выражения с помощью программы «Пошаговое решение математических задач»
Процесс факторизации необходим для упрощения многих алгебраических выражений и является полезный инструмент для решения уравнений более высокой степени. На самом деле процесс факторизации настолько важен, что очень мало алгебры, кроме этого пункта, можно выполнить без его понимания.
В предыдущих главах различие между условий и факторов было подчеркнуто. Вы должны помнить, что члены складываются или вычитаются, а множители умножаются. Далее следуют три важных определения.
Термины встречаются в указанной сумме или разнице. Факторы встречаются в указанном продукте.
Выражение находится в факторизованной форме , только если все выражение является указанным произведением.
Обратите внимание, что в этих примерах мы всегда должны учитывать выражение целиком. Факторы могут состоять из терминов, а термины могут содержать факторы, но факторизованная форма должна соответствовать приведенному выше определению.
Факторинг — это процесс преобразования суммы или разности выражений в произведение факторов.
Обратите внимание, что в этом определении подразумевается, что значение выражения не изменяется — только его форма.
УДАЛЕНИЕ ОБЩИХ ФАКТОРОВ
ЦЕЛИ
По завершении этого раздела вы сможете:
- Определите, какие факторы являются общими для всех членов выражения.
- Фактор общих факторов.
В предыдущей главе мы умножили такое выражение, как 5(2x + 1), чтобы получить 10x + 5. Обычно факторизация «отменяет» умножение. Каждый член 10x + 5 имеет множитель 5, а 10x + 5 = 5 (2x + 1).
Чтобы разложить выражение на множители, удалив общие множители, действуйте, как в примере 1.
| 3x — наибольший общий множитель всех трех членов. |
Затем найдите факторы, общие для всех терминов, и отыщите наибольший из них. Это самый большой общий фактор. В этом случае наибольший общий делитель равен 3x.
Продолжайте, поставив 3x перед скобками.
Члены в скобках находятся путем деления каждого члена исходного выражения на 3x.
| Обратите внимание, что это свойство распределения. Это обратный процесс, который мы использовали до сих пор. |
Исходное выражение теперь преобразуется в факторизованную форму. Чтобы проверить факторинг, имейте в виду, что факторинг изменяет форму, но не значение выражения. Если ответ правильный, то должно быть верно, что . Умножьте, чтобы увидеть, что это правда. Вторая проверка также необходима для факторинга — мы должны быть уверены, что выражение было полностью факторизовано. Другими словами: «Удалили ли мы все общие факторы? Можем ли мы еще добавить факторы?»
Другими словами: «Удалили ли мы все общие факторы? Можем ли мы еще добавить факторы?»
Если бы мы удалили только множитель «3» из 3x 2 + 6xy + 9xy 2 , ответ был бы
3(x 2 + 2xy + 3xy 2 ).
Умножая для проверки, мы находим, что ответ на самом деле равен исходному выражению. Однако фактор x по-прежнему присутствует во всех терминах. Следовательно, выражение не является полностью факторизованным.
| Это выражение факторизовано, но не полностью. |
Чтобы факторинг был правильным, решение должно соответствовать двум критериям:
- Должна быть возможность умножить факторизованное выражение и получить исходное выражение.
- FВыражение должно быть полностью разложено на .
Пример 2 Коэффициент 12x 3 + 6x 2 + 18x.
Решение
На данный момент нет необходимости перечислять факторы
каждого термина. Вы должны быть в состоянии мысленно определить наибольший общий множитель. Хорошей процедурой для подражания является продумывание элементов по отдельности. Другими словами, не пытайтесь сразу получить все общие множители, а сначала получите число, а затем каждую соответствующую букву. Например, 6 — это множитель 12, 6 и 18, а x — множитель каждого члена. Отсюда 12x 3 + 6х 2 + 18х = 6х(2х 2 + х + 3). Умножая, мы получаем оригинал и видим, что члены в скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.
Вы должны быть в состоянии мысленно определить наибольший общий множитель. Хорошей процедурой для подражания является продумывание элементов по отдельности. Другими словами, не пытайтесь сразу получить все общие множители, а сначала получите число, а затем каждую соответствующую букву. Например, 6 — это множитель 12, 6 и 18, а x — множитель каждого члена. Отсюда 12x 3 + 6х 2 + 18х = 6х(2х 2 + х + 3). Умножая, мы получаем оригинал и видим, что члены в скобках не имеют другого общего множителя, поэтому мы знаем, что решение правильное.
| Спросите себя: «Каков наибольший общий делитель чисел 12, 6 и 18?» |
| Затем «Каков наибольший общий делитель x 3 , x 2 и x?» |
Помните, это проверка, чтобы убедиться, что мы правильно рассчитали. |
| Снова умножьте в качестве чека. |
| Снова найдите наибольший общий делитель чисел и каждой буквы в отдельности. |
Если выражение нельзя разложить на множители, говорят, что оно простое .
| Помните, что 1 всегда является делителем любого выражения. |
ФАКТОРИЗАЦИЯ ПО ГРУППИРОВКЕ
ЗАДАЧИ
После заполнения этого раздела вы сможете:
- Факторные выражения, когда общий фактор включает более одного термина.
- Фактор по группировке.
Расширение идей, представленных в предыдущем разделе, относится к методу факторизации, называемому группировкой .
Во-первых, мы должны отметить, что общий множитель не обязательно должен быть одним термином. Например, в выражении 2y(x + 3) + 5(x + 3) есть два члена. Это 2y(x + 3) и 5(x + 3). В каждом из этих терминов у нас есть множитель (x + 3), состоящий из термов. Этот множитель (x + 3) является общим множителем.
Например, в выражении 2y(x + 3) + 5(x + 3) есть два члена. Это 2y(x + 3) и 5(x + 3). В каждом из этих терминов у нас есть множитель (x + 3), состоящий из термов. Этот множитель (x + 3) является общим множителем.
Иногда, когда имеется четыре или более терминов, мы должны вставить один или два промежуточных шага для факторизации.
Решение
Во-первых, обратите внимание, что не все четыре члена в выражении имеют общий делитель, но некоторые из них имеют. Например, мы можем разложить первые два члена на 3, что даст 3(ax + 2y). Если мы разложим a из оставшихся двух членов, мы получим a (ax + 2y). Теперь выражение равно 3(ax + 2y) + a(ax + 2y), и у нас есть общий множитель (ax + 2y), и мы можем разложить как (ax + 2y)(3 + a). Умножая (ax + 2y)(3 + a), мы получаем исходное выражение 3ax + 6y + a 2 x + 2ay и убедитесь, что факторинг правильный.
Это пример разложения на множители путем группировки , поскольку мы «сгруппировали» термины по два за раз.
| Умножьте (x — y)(a + 2) и посмотрите, получится ли исходное выражение. Опять умножить как чек. |
Иногда члены должны быть сначала переупорядочены, прежде чем можно будет выполнить разложение по группам.
Пример 7 Коэффициент 3ax + 2y + 3ay + 2x.
Решение
Первые два члена не имеют общего делителя, но первый и третий члены имеют, поэтому мы переставим члены так, чтобы третий член располагался после первого. Всегда смотрите вперед, чтобы увидеть порядок, в котором термины могут быть расположены.
Во всех случаях важно убедиться, что коэффициенты в скобках абсолютно одинаковы. Это может потребовать факторизации отрицательного числа или буквы.
| Помните, свойство коммутативности позволяет нам переставлять эти термины. Умножить как чек. |
Пример 8 Коэффициент ax — ay — 2x + 2y.
Решение
Обратите внимание, что если мы разложим a из первых двух членов, мы получим a(x — y). Глядя на последние два члена, мы видим, что разложение на множители +2 даст 2(-x + y), но разложение на множители «-2» дает -2(x — y). Мы хотим, чтобы члены в круглых скобках были (x — y), поэтому мы действуем таким образом.
ФАКТОРИЗАЦИЯ ТРЕХНОМОВ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Умножьте в уме два двучлена.
- Разложите на множители трехчлен с коэффициентом первого члена, равным 1.
- Найдите делители любого факторизуемого трехчлена.
Большое количество будущих задач будет связано с разложением трехчленов на множители как произведений двух двучленов. В предыдущей главе вы научились умножать многочлены. Теперь мы хотим рассмотреть частный случай умножения двух двучленов и разработать шаблон для этого типа умножения.
Поскольку этот тип умножения очень распространен, полезно иметь возможность найти ответ, не выполняя так много шагов. Давайте посмотрим на шаблон для этого.
Давайте посмотрим на шаблон для этого.
Из примера (2x + 3)(3x — 4) = 6x 2 + x — 12 обратите внимание, что первый член ответа (6x 2 ) получен из произведения двух первых членов множители, то есть (2x)(3x).
Также обратите внимание, что третий член (-12) получен из произведения вторых членов факторов, то есть (+ 3)(-4).
Теперь у нас есть следующая часть шаблона:
Теперь снова взглянув на пример, мы видим, что средний член (+x) получен из суммы двух произведений (2x)(-4) и (3)(3x).
Теперь для любых двух биномов у нас есть следующие четыре произведения:
- Первый срок за первым сроком
- Внешние условия
- Внутренние условия
- Последний срок за последним сроком
Эти продукты показаны этим шаблоном.
Когда произведения внешних членов и внутренних членов дают одинаковые члены, их можно объединить, и решение будет трехчленным.
| Этот метод умножения двух двучленов иногда называют методом FOIL. FOIL расшифровывается как First, Outer, Inner, Last. Это упрощенный метод умножения двух двучленов, и его полезность будет видна, когда мы разложим трехчлены. |
Вы должны запомнить эту схему.
| Опять же, возможно, запоминание слова ФОЛЬГА поможет. |
Этот образец следует не только запомнить, но и научиться переходить от задачи к ответу без каких-либо письменных шагов. Этот умственный процесс умножения необходим, если мы хотим достичь мастерства в факторинге.
Работая над следующими упражнениями, попытайтесь найти правильный ответ, ничего не записывая, кроме самого ответа. Чем больше вы практикуете этот процесс, тем лучше у вас будет факторинг.
Теперь, когда мы установили схему умножения двух двучленов, мы готовы разложить трехчлены на множители. Сначала мы рассмотрим разложение на множители только тех трехчленов, у которых коэффициент первого члена равен 1.
Сначала мы рассмотрим разложение на множители только тех трехчленов, у которых коэффициент первого члена равен 1.
Решение
Поскольку это трехчлен и не имеет общего делителя, мы будем использовать схему умножения для факторизации.
| На самом деле мы будем работать в обратном порядке по сравнению с предыдущим упражнением. |
Сначала распишите задачу в скобках.
Теперь мы хотим заполнить термины так, чтобы шаблон давал исходный трехчлен при умножении. Первый член прост, поскольку мы знаем, что (x)(x) = x 2 .
| Помните, произведение первых двух членов двучлена дает первый член трехчлена. |
Теперь мы должны найти числа, которые при умножении дают 24 и в то же время складывают, чтобы получить средний член. Обратите внимание, что в каждом из следующих у нас будет правильный первый и последний термин.
Только последний продукт имеет средний член 11x, и правильное решение
Этот метод факторинга называется методом проб и ошибок — по понятным причинам.
Здесь могут быть полезны некоторые числовые факты из арифметики.
Следовательно, когда мы факторизуем такое выражение, как x 2 + 11x + 24, мы знаем, что произведение двух последних членов бинома должно быть 24, что является четным, а их сумма должна быть равна 11, что является нечетным. |
Решение
Здесь проблема немного другая. Мы должны найти числа, которые при умножении дают 24 и при этом при сложении дают — 11. Всегда нужно помнить о закономерности. Последний член получается строго путем умножения, а средний член получается, наконец, из суммы. Зная, что произведение двух отрицательных чисел положительно, а сумма двух отрицательных чисел отрицательна, получаем
Решение
Здесь мы сталкиваемся с отрицательным числом для третьего слагаемого, и это несколько усложняет задачу. сложно. Поскольку -24 может быть только произведением положительного числа и отрицательного числа, а средний член должен исходить из суммы этих чисел, мы должны мыслить в терминах различия. Мы должны найти числа, произведение которых равно 24 и которые отличаются на 5. Кроме того, большее число должно быть отрицательным, потому что, когда мы складываем положительное и отрицательное число, ответ будет иметь знак большего. Учитывая все это, получаем
Порядок факторов не имеет значения. по коммутативному закону умножения. |
Следующие пункты помогут вам разложить трехчлены на множители:
- Когда знак третьего члена положителен, оба знака в множителях должны быть одинаковыми — и они должны быть подобны знаку среднего члена.
- Когда знак последнего члена отрицательный, знаки множителей должны быть разными, а знак большего члена должен быть подобен знаку среднего члена.
В предыдущем упражнении коэффициент каждого из первых слагаемых был равен 1. Когда коэффициент первого слагаемого не равен 1, проблема факторинга значительно усложняется, поскольку число возможностей значительно увеличивается.
| Выполнив предыдущий набор упражнений, вы теперь готовы попробовать еще несколько сложных трехчленов. |
Обратите внимание, что есть двенадцать способов получить первый и последний члены, но только один из них имеет 17x в качестве среднего члена.
| Вы, конечно, могли бы попробовать каждое из них мысленно вместо того, чтобы записывать их. |
Есть только один способ получить все три условия:
В этом примере одна из двенадцати возможностей верна. Таким образом, проб и ошибок может занять очень много времени.
Несмотря на то, что используемый метод представляет собой метод угадывания, это должно быть «обоснованное угадывание», в котором мы применяем все наши знания о числах и упражняемся в умственной арифметике. В предыдущем примере мы бы сразу отбросили многие комбинации. Поскольку мы ищем 17x в качестве среднего члена, мы не будем пытаться использовать те возможности, которые умножают 6 на 6, или 3 на 12, или 6 на 12 и т. д., поскольку эти произведения будут больше 17. Кроме того, поскольку 17 нечетно, мы знаем, что это сумма четного числа и нечетного числа. Все эти вещи помогают сократить количество возможных попыток.
| Сначала найдите числа, которые дают правильный первый и последний члены трехчлена. Затем добавьте внешний и внутренний продукт, чтобы проверить правильность среднего члена. |
Решение
Сначала мы должны проанализировать проблему.
- Последний член положительный, поэтому два одинаковых знака.
- Средний член отрицательный, поэтому оба знака будут отрицательными.
- Множители 6×2 равны x, 2x, 3x, 6x. Делители 15 равны 1, 3, 5, 15.
- Исключить как слишком большое произведение 15 на 2x, 3x или 6x. Попробуйте несколько разумных комбинаций.
| Это автоматически дало бы слишком большой средний член. |
| Посмотрите, как сокращается количество возможностей. |
Раствор
Анализ:
- Последний член отрицательный, поэтому отличается от знаков.

- Мы должны найти произведения, отличающиеся на 5 с большим отрицательным числом.
- Мы исключаем произведение 4x и 6 как возможно слишком большое.
- Попробуйте несколько комбинаций.
| Помните, мысленно попробуйте различные возможные комбинации, которые являются разумными. Это процесс факторинга методом проб и ошибок. Вы станете более опытным в этом процессе благодаря практике. |
(4x — 3)(x + 2): Здесь средний член равен + 5x, что является правильным числом, но неправильным знаком. Будьте осторожны, чтобы не принять это как решение, а поменяйте знаки так, чтобы большее произведение совпадало по знаку со средним членом.
К тому времени, когда вы закончите следующий набор упражнений, вы должны чувствовать себя намного более комфортно при разложении трехчлена на множители. |
ОСОБЫЕ СЛУЧАИ В ФАКТОРИНГЕ
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Определите и разложите на множители разности двух полных квадратов.
- Определите и разложите на множители совершенный квадратный трехчлен.
В этом разделе мы хотим рассмотреть некоторые частные случаи факторинга, которые часто встречаются в задачах. Если эти особые случаи признаются, факторинг значительно упрощается.
Первый частный случай, который мы обсудим, это разность двух полных квадратов .
Напомним, что при умножении двух двучленов на шаблон средний член получается из суммы двух произведений.
Из нашего опыта работы с числами мы знаем, что сумма двух чисел равна нулю только в том случае, если эти два числа являются отрицательными по отношению друг к другу.
Когда сумма двух чисел равна нулю, одно из чисел называется аддитивным обратным другого. Например: ( + 3) + (-3) = 0, поэтому + 3 является аддитивной инверсией — 3, также -3 является аддитивной инверсией +3. |
В каждом примере средний член равен нулю. Обратите внимание, что если два двучлена умножаются, чтобы получить двучлен (средний член отсутствует), они должны быть в форме (a — b) (a + b).
| Правило можно записать как = (a — b)(a + b). Это форма, которую вы найдете наиболее полезной в факторинге. |
Чтение этого правила справа налево говорит нам, что если у нас есть проблема для факторизации и если она имеет форму , факторы будут (a — b)(a + b).
Решение
Здесь оба члена являются полными квадратами и разделены знаком минус.
| Где a = 5x и b = 4. |
Особые случаи действительно облегчают факторинг, но не забудьте признать, что особый случай — это именно то, что он очень особенный. В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разность двух полных квадратов».
В этом случае оба члена должны быть полными квадратами, а знак должен быть отрицательным, отсюда «разность двух полных квадратов».
| Сумма двух квадратов не разлагается. |
Вы также должны быть осторожны, чтобы распознать правильные квадраты. Помните, что совершенные квадратные числа — это числа, квадратные корни которых являются целыми числами. Кроме того, совершенные квадратные показатели четны.
| Студенты часто упускают из виду тот факт, что (1) — совершенный квадрат. Таким образом, такое выражение, как x 2 — 1, представляет собой разность двух полных квадратов и может быть факторизовано этим методом. |
Другим частным случаем факторинга является трехчлен с совершенным квадратом. Заметьте, что возведение бинома в квадрат приводит к этому случаю.
Мы узнаем этот случай, отмечая особенности. Три вещи очевидны.
Три вещи очевидны.
- Первый член — полный квадрат.
- Третий член — полный квадрат.
- Средний член равен удвоенному произведению квадратного корня из первого и третьего членов.
| Для целей факторинга удобнее записать оператор как |
Решение
- 25x 2 — это совершенный квадратный главный квадратный корень = 5x.
- 4 — это совершенный квадратный главный квадратный корень = 2.
- 20x — удвоенное произведение квадратных корней из 25x 2 и
- 20х = 2(5х)(2).
Чтобы разложить на множители идеальный квадратный трехчлен , сформируйте двучлен с квадратным корнем из первого члена, квадратным корнем из последнего члена и знаком среднего члена и укажите квадрат этого двучлена.
Таким образом, 25x 2 + 20x + 4 = (5x + 2) 2
Всегда возводите бином в квадрат, чтобы убедиться, что средний член правильный. |
Не частный случай совершенного квадратного трехчлена.
| 15 ≠ 2(2x)(3) |
ДОПОЛНИТЕЛЬНЫЕ КОРРЕКТЫ ДЛЯ ФАКТОРИНГА ПРОБ И ОШИБОК
ЦЕЛИ
По завершении этого раздела вы сможете:
- Найдите ключевое число трехчлена.
- Используйте номер ключа, чтобы разложить трехчлен на множители.
В этом разделе мы хотим обсудить некоторые упрощения метода проб и ошибок. Они необязательны по двум причинам. Во-первых, некоторые могут предпочесть пропустить эти методы и просто использовать метод проб и ошибок; во-вторых, эти сокращения не всегда практичны для больших чисел. Однако они увеличат скорость и точность для тех, кто их освоит.
Первым шагом в этих сочетаниях клавиш является поиск номер ключа . После того, как вы нашли номер ключа, его можно использовать более чем одним способом.
В разлагаемом на множители трехчлене ключевое число есть произведение коэффициентов первого и третьего членов.
| Произведение этих двух чисел является «ключевым числом». |
Первое использование номера ключа показано в примере 3.
Решение
Шаг 1 Найдите номер ключа. В этом примере (4)(-10)=-40.
Шаг 2 Найдите множители ключевого числа (-40), которые в сумме дадут коэффициент среднего члена ( + 3). В этом случае (+8)(-5)=-40 и (+8)+(-5)=+3.
Шаг 3 Множители ( + 8) и ( — 5) будут перекрестными произведениями в схеме умножения.
| Произведение этих двух чисел является «ключевым числом». |
Шаг 4 Используя только внешнее перекрестное произведение, найдите множители первого и третьего членов, которые при умножении дают произведение. В этом примере мы должны найти множители 4×2 и -10, которые при умножении дают +8x. Это 4x от 4×2 и (+2) от (-10).
Это 4x от 4×2 и (+2) от (-10).
Поместите эти множители на первую и последнюю позиции в шаблоне
| Есть только один способ сделать это правильно. |
Шаг 5 Забудьте номер ключа на этом этапе и вернитесь к исходной проблеме. Поскольку первая и последняя позиции заполнены правильно, теперь необходимо заполнить только две другие позиции.
| Опять же, это можно сделать только одним способом. |
Мы знаем, что произведение двух первых слагаемых должно давать 4×9.0445 2 и 4x уже на месте. Нет другого выбора, кроме х.
Обратите внимание, что на шаге 4 мы могли бы начать с внутреннего продукта вместо внешнего продукта. Мы получили бы те же коэффициенты. Наиболее важным является систематический процесс факторинга. Наиболее важным является систематический процесс факторинга. |
Мы знаем, что произведение двух вторых членов должно быть (-10) и (+2) уже на месте. У нас нет другого выбора, кроме как (- 5).
| Помните, что если трехчлен можно разложить на множители, то существует только один возможный набор множителей. |
| Если не удается найти делителей ключевого числа, сумма которых является коэффициентом при средних членах, то трехчлен является простым и не делит. |
Второе использование номера ключа в качестве ярлыка включает факторинг путем группирования. Работает как в примере 5.
Решение
Шаг 1 Найдите число ключа (4)(-10) = -40.
Шаг 2 Найдите множители (-40), которые в сумме дадут коэффициент среднего члена (+3).
| Шаги 1 и 2 в этом методе такие же, как и в предыдущем методе. |
Шаг 3 Перепишите исходную задачу, разбив средний член на две части, найденные в шаге 2. 8x — 5x = 3x, так что мы можем написать
Шаг 4 Разложите эту задачу из шага 3 по метод группировки, изученный в разделе 8-2
| Теперь это становится обычной задачей факторизации по группировке. |
Следовательно,
| Опять же, существует только одна возможная пара множителей, которые можно получить из данного трехчлена. |
Помните, что если шаг 2 невозможен, трехчлен является простым и не может быть разложен на множители. |
ПОЛНАЯ ФАКТОРИЗАЦИЯ
ЦЕЛИ
По завершении этого раздела вы сможете разложить трехчлен на множители, выполнив следующие два шага:
- Сначала найдите общие факторы.
- Разложите на множители оставшийся трехчлен, применяя методы, описанные в этой главе.
Итак, мы изучили все обычные методы факторизации, встречающиеся в элементарной алгебре. Однако вы должны знать, что для решения одной проблемы может потребоваться более одного из этих методов. Помните, что существует две проверки правильности факторинга.
- Будут ли множители умножаться, чтобы дать исходную задачу?
- Все ли множители простые?
| Как только общий множитель найден, вы должны проверить, является ли полученный трехчлен факторизуемым. |
Если у трехчлена есть какие-либо общие делители, обычно проще сначала разложить их на множители. |
При разложении на множители рекомендуется всегда сначала удалять наибольший общий множитель, а затем, если возможно, факторизовать то, что осталось.
РЕЗЮМЕ
Ключевые слова
- Выражение находится в факторизованной форме, только если все выражение является указанным произведением.
- Факторинг — это процесс, который превращает сумму или разность условий в произведение факторов.
- Простое выражение нельзя разложить на множители.
- Наибольший общий делитель — это наибольший общий делитель всех терминов.
- Выражение является полностью разложенным на множители , когда дальнейшее разложение на множители невозможно.
- Возможность факторизации путем группировки существует, когда выражение содержит четыре или более членов.
- Метод FOIL можно использовать для умножения двух двучленов.
- Особые случаи факторинга включают разность двух квадратов и трехчленов с совершенными квадратами .
