Содержание
Урок математики в 1-м классе по теме «Классификация линий по самостоятельно выделенным признакам»
Цели урока:
- создать условия для формирования первичного
представления о луче, научить различать прямую
линию, отрезок, луч, проверить степень усвоения
детьми ранее данной информации; - развивать память, внимание, мышление, умение
наблюдать, сравнивать, классифицировать,
анализировать и обобщать, развивать
интеллектуальные и практические умения детей; - воспитывать активную личность.
Оборудование: Интерактивная доска,
раздаточный геометрический материал у детей,
словарь русского языка.
Ход урока
1. Организационный момент.
СЛАЙД № 1.
Учитель: Здравствуйте, ребята! Всем известно,
что у нас самый лучший в мире класс! Мальчики
здесь? Девочки здесь? Готовы к уроку математики?
2. Актуализация базовых знаний.
Актуализация базовых знаний.
СЛАЙД №2.
Я очень рада видеть ваши добрые, веселые глаза.
Вижу, что вы готовы к работе. И сегодня мы с вами
отправляемся в очередное путешествие по Великой
стране Математики и побываем в уже известном нам
городе Геометрии. Нашим экскурсоводом будет
Карандаш. Со многими жителями города вы уже
знакомы и сможете без труда их узнать.
СЛАЙД №3.
Игра: «Узнай меня».
Учитель: Поиграем в игру: «Узнай меня». У вас у
каждого на столе конверт, возьмите из него
геометрические фигуры. Я загадываю загадку, а вам
нужно показать нам фигуру-отгадку. (На партах у
каждого ребенка набор геометрических фигур.)
— Я — многоугольник, имею 3 стороны. Как меня
зовут?
(Учащиеся выбирают из раздаточного материала
треугольник и показывают его учителю. Учитель
открывает на интерактивной доске по очереди все
названные фигуры)
— Я — многоугольник, у меня 4 равные стороны.
(квадрат)
— А вот я — вообще не многоугольник. Зато у меня
можно найти в часах, в машине, в чашке, на меня
даже солнышко издали похоже. Кто же я? (круг)
— А вот я ни многоугольник и ни круг. Я линия
ровная, у которой нет начала и нет конца. Кто я?
(прямая)
— Я самая маленькая геометрическая фигура Кто я?
(точка)
-А вот я часть прямой, у меня есть начало и есть
конец. Кто же я? (Отрезок) Назовём хором все
фигуры. Будьте внимательны (Показываю не по
порядку)
Вывод: Мы сделали разминку. Для чего? (Дети:
Чтобы знать и различать геометрические фигуры,
настроиться на работу, сосредоточиться:)
Учитель: Чем похожи все фигуры?
Дети: Они все одного цвета.
Учитель: Чем отличаются?
Дети: Они имеют разную форму.
Дети: Они разного размера.
Вывод: Все предметы можно сравнивать по цвету,
размеру, форме.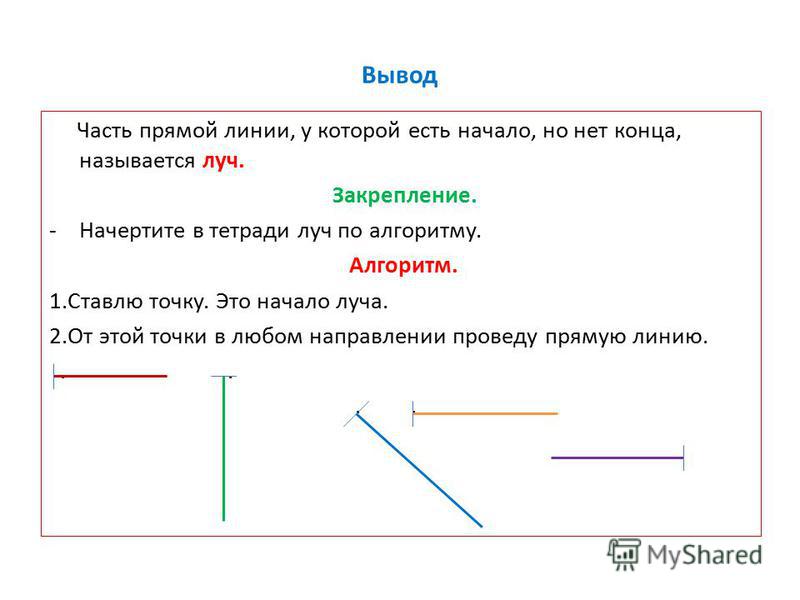
Учитель:
Какая фигура лишняя? Почему?
Дети: Лишняя фигура — линия, т.к. её можно
продолжить, а остальные фигуры замкнутые.
ФИЗМИНУТКА.
(Гимнастика для глаз по методу Г. А. Шичко.)
Учитель: Продолжаем работу. Сколько фигур
слева? (2) Сколько справа? (4) А где фигур меньше?
(Слева). Значит справа фигур больше. Какое задание
можно выполнить с этими числами?
Дети: Сложить, вычесть, поставить знак.
Учитель: Какой знак? Дорожный, восклицательный?
Дети: Нет. Математический. Когда сравнивают
числа на письме, то ставят математический знак
сравнения.
СЛАЙД № 4.
Учитель: Работа с интерактивной доской. Какой
знак поставим между числами? Если так, то
хлопните, а если не так, то молчите. (Исчезающий
карандаш)
2 > 4 2 = 4
2 < 4
Волшебный карандаш с вами согласен. Как
называется эта запись? (Неравенство) А что такое
неравенство? А где мы можем узнать?
Дети: Спросить у взрослых, у учителя, посмотреть
в толковом словаре русского языка. Неравенство -
Неравенство -
в математике это соотношение между величинами,
показывающее, что одна величина больше или
меньше другой.
Учитель: А для чего мы вспомнили о неравенствах?
Дети: Нам пригодится.
Учитель: Молодцы. Все с заданием справились. А
еще, ребята, у данных фигур был разный характер.
Круг был веселее, чем треугольник, а треугольник
веселее, чем квадрат. Кто был самый веселый?
Дети: Круг.
Учитель: А кто самый грустный?
Дети: Квадрат.
Учитель: Хочу пожелать, чтобы и у вас и у наших
гостей было хорошее настроение. А мы сделаем
весёлую физминутку.(Если я показываю весёлое
лицо, то вам надо хлопнуть 3 раза, а если грустное
— 3 раза присесть.
СЛАЙД № 5.
Учитель: А теперь продолжим наше путешествие.
Вместе с нашим экскурсоводом Карандашом
отправимся на проспект Линейный. Здесь живут
веселые и добрые наши друзья.
Как вы думаете, кто живёт в этих домиках?
Дети: В этих домах живут прямые линии.
Дети: Там еще живет отрезок.
Дети: Там живут прямые и кривые линии.
Учитель: Молодцы! А кто живёт здесь?
Дети: Не знаем.
Учитель: Как вы думаете, какова будет тема
нашего сегодняшнего урока?
Дети: Познакомиться с новой геометрической
фигурой.
Учитель: Какие цели поставим перед собой?
СЛАЙД № 6.
Дети:
1). Познакомиться с новой геометрической
фигурой.
2). Быть внимательными, умными,
сосредоточенными.
3). Хорошо работать, слушать и слышать учителя.
Учитель: А я вам в этом помогу. Сейчас мы с
ребятами (инсценировка) расскажем историю,
которая случилась с Карандашом. А вы нам будете
помогать. Договорились?
СЛАЙД № 6.
3. Выход на тему урока.
Учитель: Вот какая история случилась с
Карандашом.
Решил однажды Карандаш прогуляться по Прямой
линии. Идет, идет, устал, а конца линии все не
видно.
— Долго ли мне еще идти? Доберусь ли я до конца? -
спрашивает он у Прямой.
Что ему ответит Прямая линия?
Дети: Карандаш, не дойдет до конца линии,
потому что у прямой нет конца.
Учитель: Правильно.
— Эх ты, у меня же нет конца, — ответила Прямая.
— Тогда я пойду в другую сторону, — сказал
Карандаш.
Дети: И в другую сторону, Карандаш, не дойдет
до конца линии, потому что у прямой нет начала и
конца.
Учитель: Верно. А Прямая, даже песенку ему спела.
— Без конца и края линия прямая,
Хоть сто лет по ней иди,
Не найдешь конца пути.
Расстроился Карандаш.
— Что же мне делать? Я не хочу ходить по линии. Я
устал.
Что вы, ребята, посоветуете Карандашу?
(Дети дают различные советы. )
)
А вы, уважаемые взрослые, что посоветуете
карандашу?
Учитель: Тогда отметь на мне 2 точки, -
посоветовала ему Прямая. Так Карандаш и сделал.
Работа с интерактивной доской.
— Ура! — Закричал Карандаш. — Появились два
конца. Теперь я могу гулять от одного конца до
другого. Но тут же задумался.
— А что же это такое на Прямой получилось?
Ребята, помогите Карандашу.
Дети: Это отрезок.
Учитель: А что вы знаете об отрезке?
Дети: Отрезок — это часть прямой. У него есть
начало и конец.
4. Изучение нового материала.
Учитель:
А однажды Карандаш решил отнять у
Прямой отрезок. Взял он с собой ножницы и
потихоньку вырезал отрезок. Только не понятно
ему, что же это такое получилось.
— А вы, ребята, знаете? Может это быть новым
отрезком?
Дети: Нет, не может. У одной линии нет начала и
У одной линии нет начала и
есть конец, а у другой — есть начало, но нет конца.
Учитель: А получилось на прямой 2 луча. У луча
есть начало, а вот конца нет.
Вывод: Как называется новая геометрическая
фигура? Что такое ЛУЧ?
5. Практическая часть.
Работа по учебнику. (И. Аргинская, Математика,
часть 1, стр. 42, №73)
Учитель: Сравни линии. Чем они похожи? Чем
отличаются? С какими линиями ты уже был знаком?
Дети: Мы знали прямую линию, отрезок.
Учитель: Обведи прямую линию синим
карандашом, отрезок — зеленым. Как называется
линия, с которой вы познакомились сегодня?
Дети: Эта линия называется лучом.
Учитель:
Найди луч и обведи его красным
карандашом.
Подумай и объясни, чем отличается луч от
прямой?. От отрезка?
От отрезка?
Учитель: Сейчас будем работать в рабочей
тетради с. 25 № 52. Здесь нам и пригодились знания о
неравенстве.
Учитель: Выполним тест. Если согласны со мной,
то хлопните, а если не согласны, то молчите. ЛУЧ -
это прямая, у которой есть начало и конец.
ЛУЧ — это прямая, у которой нет начала и нет
конца.
ЛУЧ — это прямая, у которой есть начало, но нет
конца.
МОЛОДЦЫ! А если кто-то ошибся, ничего страшного,
ведь мы в школе только учимся. В следующий раз
обязательно получится. Вспомним, какие цели
ставили в начале урока. Каждый молча вспоминает
свои цели. Кто справился, поднимите руку. Луч
приготовил для вас загадку.
Среди поля голубого —
Яркий блеск огня большого.
Не спеша огонь тут ходит,
Землю-матушку обходит,
Светит весело в оконце.
Ну, конечно, это ::.
Дети: Солнце.
Учитель: А почему Луч загадал вам загадку про
солнышко?
Дети: Потому что у солнышка тоже есть лучи.
РЕФЛЕКСИЯ.
Учитель: Дети, у вас на партах тоже есть 2
солнечных луча. Если вам было интересно на уроке
и всё получалось, то выберите жёлтый луч, а если
было интересно, но вы в чём-то затруднялись -
красный. Добавим лучи нашему весёлому кругу. И
получим весёлое солнышко.
Вывод: Молодцы! У каждого лучика есть начало, но
нет конца. Так и у вас 1 класс — это только начало
и ещё очень много нового и интересного в своей
жизни вы узнаете в школе. И на память о нашем
сегодняшнем путешествии я хочу вам подарить
солнышко, которое есть у вас в конверте, а второе
солнышко подарите нашим гостям.
6. Итог урока.
Учитель: Вот и закончилось наше воображаемое
путешествие. Мы прощаемся с городом Геометрией,
его прекрасными жителями — геометрическими
фигурами. Давайте еще раз вспомним, что же мы
знает про прямую линию, отрезок и луч.
Дети: У прямой нет начала и нет конца.
Дети: У отрезка есть начало и есть конец.
Дети:
А у луча есть начало и нет конца.
Учитель:
Надеюсь, наше путешествие было
увлекательным и интересным. Давайте улыбнемся на
прощание всем обитателям волшебной страны
Математики, друг другу и порадуемся нашим
успехам. Но это лишь малая часть того, что можно
узнать на уроках математики. Впереди вас ждет еще
много путешествий по Великой стране, название
которой: Математика.
Приложение.
Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABC
точка 1, точка 2, точка 3
123
Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А".Но как понять через какие? AAA
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abc
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
a
прямая линия AB
BA
Прямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча
A
A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
a
луч AB
BA
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBA
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BA
прямая линия AB
BA
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
✂
BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BA
Задача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная.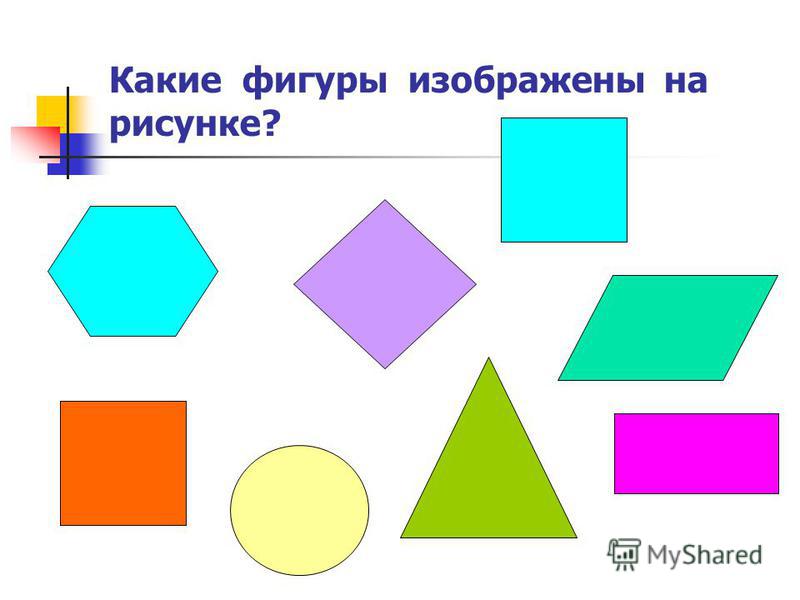 Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см.У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
строк — SSAT Elementary Level Math
Все математические ресурсы SSAT Elementary Level
12 диагностических тестов
526 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 Следующая →
SSAT Elementary Level Math Help »
Геометрия »
Плоская геометрия »
Строки
Что верно для луча?
Возможные ответы:
Луч бесконечно распространяется в обоих направлениях.
Луч — это линия с начальной точкой, но без конечной.
Луч имеет три конца.
Луч всегда короче отрезка.
Луч всегда имеет форму круга.
Правильный ответ:
Луч — это линия с начальной точкой, но без конечной.
Объяснение:
Луч всегда имеет одну начальную точку, а затем бесконечно продолжается в противоположном направлении. Сегменты линии отличаются тем, что они имеют определенную начальную и конечную точки.
Сообщить об ошибке
Алекс нужно купить забор для своего двора. Она не знает, сколько ей нужно, чтобы окружить весь двор. Что ей нужно рассчитать, чтобы понять это?
Возможные ответы:
Высота ограждения
Площадь двора
Периметр двора
Том двора
Правильный ответ:
Периметр из двора
Объяснение:
Периметр — это расстояние вокруг фигуры. Ей нужно знать периметр своего двора, чтобы определить, сколько забора нужно купить.
Сообщить об ошибке
Линия переменного тока имеет длину 12 дюймов. Если точка В находится в центре линии АС, сколько дюймов в длину составляет линия ВС?
Если точка В находится в центре линии АС, сколько дюймов в длину составляет линия ВС?
Возможные ответы:
Правильный ответ:
Пояснение:
Так как точка B находится в середине линии AC, она разбивает линию AC на два равных отрезка — линию AB и линию BC. Мы должны разделить исходную длину линии AC на 2, потому что мы разрываем исходную линию пополам.
Сообщить об ошибке
Длина линии на числовой прямой составляет дюймы. Если начальная точка равна , то какая конечная точка на числовой прямой?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы должны добавить начальную точку к длине линии, чтобы найти конечную точку линии.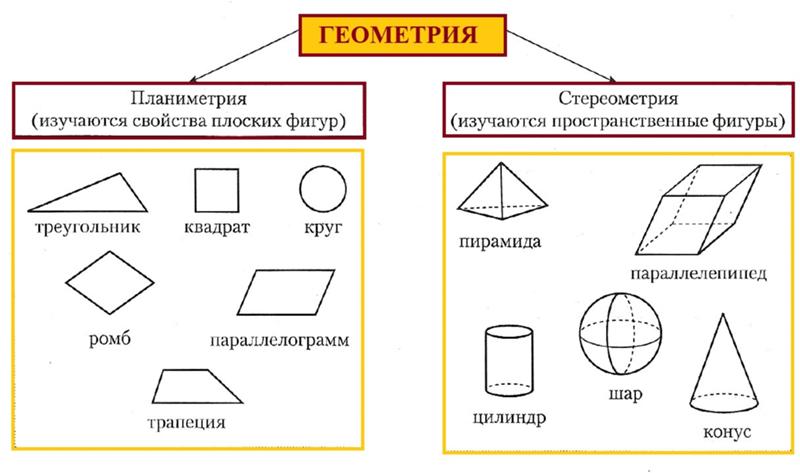
Сообщить об ошибке
Пятиугольник имеет ____ сторон.
Возможные ответы:
Правильный ответ:
Пояснение:
Пятиугольник имеет пять сторон.
Сообщить об ошибке
Линия переменного тока имеет длину 24 дюйма. Если точка B является серединой линии AC, то сколько дюймов будет длина линии BC?
Возможные ответы:
Правильный ответ:
Объяснение:
Точка B — это середина, которая разбивает линию AC на два отрезка равной длины. Следовательно, чтобы найти длину линии BC, нужно длину линии AC разделить на 2:9.0005
Сообщить об ошибке
Что такое отрезок?
Возможные ответы:
Часть прямой, соединяющая две точки.
Линия, имеющая начальную точку, но не имеющая конечной точки.
Линия, длина которой всегда меньше 10 сантиметров.
Линия, длина которой всегда превышает 10 сантиметров.
Линия, не имеющая начальной и конечной точек.
Правильный ответ:
Часть прямой, соединяющая две точки.
Объяснение:
Отрезок — это часть прямой, соединяющая две точки. Он отличается от линии и луча тем, что имеет определенные начальную и конечную точки.
Сообщить об ошибке
Какое утверждение относительно сегментов линий является верным?
Возможные ответы:
Отрезок кривой.
Отрезок линии проходит в обоих направлениях без конечных точек.
Сегмент линии имеет три конечные точки.
Отрезок линии — это «кусок» линии, имеющий две конечные точки.
Отрезок линии имеет одну конечную точку, но бесконечно продолжается в одном направлении.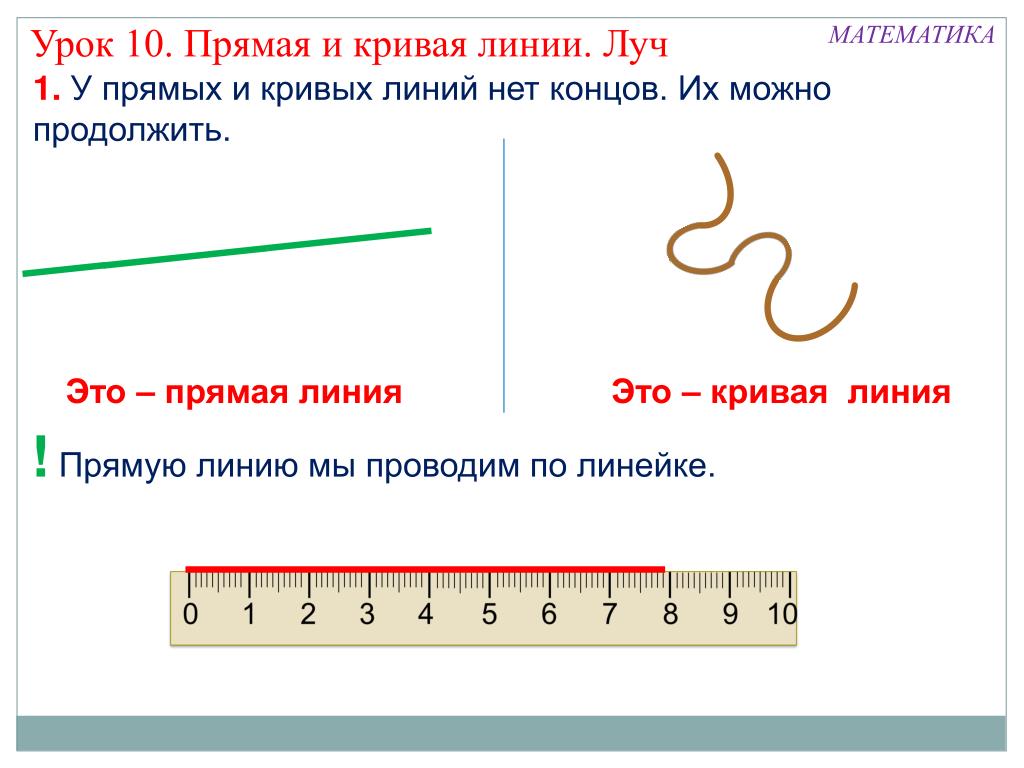
Правильный ответ:
Отрезок прямой — это «кусок» прямой, имеющий две конечные точки.
Объяснение:
Отрезок линии — это часть линии, соединенная двумя конечными точками.
Сообщить об ошибке
Линия подключена от к . Какова длина линии?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите формулу расстояния.
Подставьте точки и решите расстояние.
Сообщить об ошибке
Найдите длину линии, которая начинается в точке (1,7) и продолжается до (9,7).
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить, просто поймите, что расстояние между этими точками будет просто разницей их значений x, поскольку их значения y остаются неизменными.
Эти точки находятся на горизонтальной линии.
Итак,
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все математические ресурсы SSAT элементарного уровня
12 Диагностические тесты
526 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Знакомство с точкой, лучом, линией и отрезком линии
Точка
Точка является основным строительным блоком геометрии. Каждая форма создается путем объединения точек.
Маленькая точка, отмеченная карандашом, является точкой. Точка не имеет ни длины, ни ширины. У него нет толщины. Точка – это метка положения. Точка указывает точное местоположение. Точка обозначается точкой (.) и именуется в алфавитном порядке.
На приведенном выше рисунке О — это точка, так как она имеет определенную отметку. Здесь это указывает на то, что эта точка O расположена в центре плоскости. На рисунке ниже есть еще одна точка А. Она расположена справа внизу плана.
На рисунке ниже есть еще одна точка А. Она расположена справа внизу плана.
Рэй
Давайте подумаем о факеле. Лучи света выходят из него и удаляются. Возьмем пример с солнцем. Лучи начинаются от солнца и идут во всех направлениях и достигают нас.
В геометрии также луч начинается из точки и может уйти в бесконечность. У него есть начальная точка, но нет конечной точки. Мы говорим, что луч имеет один конец и идет без конца в одном направлении.
На рисунке выше начало от A, а стрелка указывает на то, что оно может идти до бесконечности.
Длина не может быть измерена. Из заданной точки можно провести неограниченное количество лучей в разных направлениях.
Лучи, исходящие от факела или солнца, являются примерами лучей.
Это луч, потому что луч имеет одну конечную точку и идет без конца в одном направлении
Линия
Посмотрите на рисунок выше. С обеих сторон есть стрелки. Это указывает на то, что он может идти дальше в обе стороны без конца.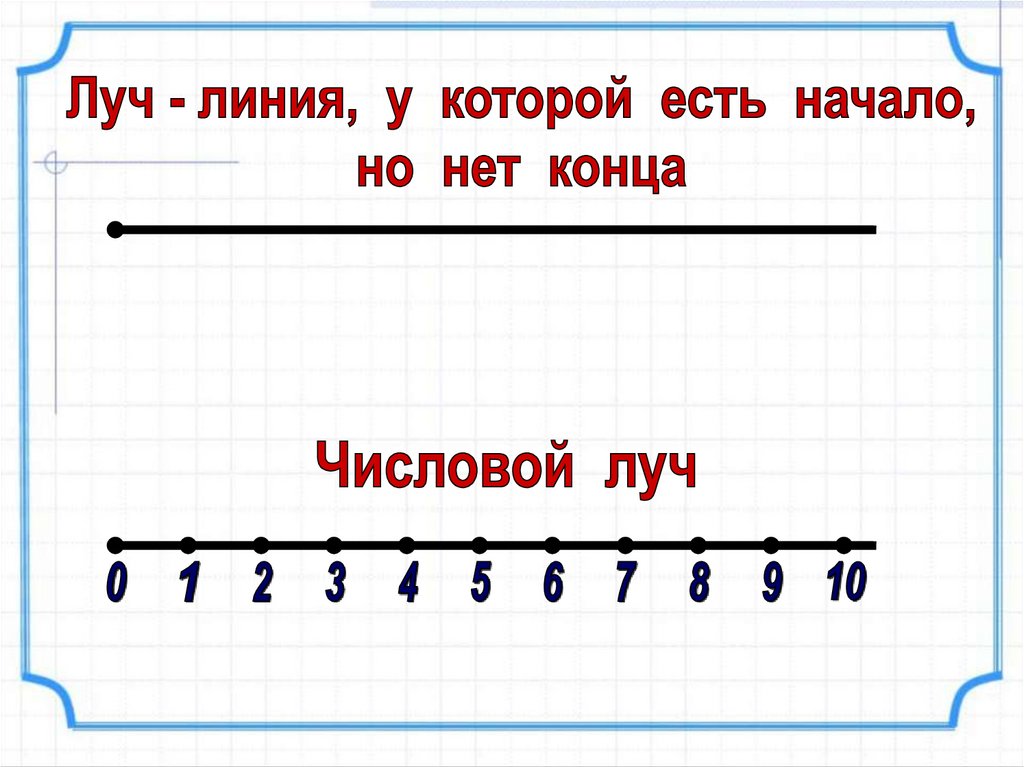 Это называется линией.
Это называется линией.
Линия идет без конца в обоих направлениях. Оба конца линии могут уйти в бесконечность. У линии нет конечных точек. Длина линии не может быть измерена. Линия не имеет определенной длины.
Линия называется по любым двум точкам на ней и записывается как линия AB или линия PQ. Через две заданные точки А и В можно провести одну и только одну прямую. Эта прямая называется АВ. Его также можно назвать БА. Линия BA такая же, как и линия AB. Оба проходят через одни и те же две точки A и B.
Через заданную точку A можно провести неограниченное количество прямых.
Горизонтальная линия проходит прямо влево или вправо поперек. Вертикальная линия идет прямо вверх или вниз.
Диагональная линия может проходить в любом направлении между горизонтальной и вертикальной линиями.
Сегмент линии
Теперь посмотрите на рисунок выше. Ни на одном конце нет стрелки. Он начинается с одной точки и заканчивается в другой точке. Это называется сегментом линии. Участок прямой – это отрезок прямой.
Это называется сегментом линии. Участок прямой – это отрезок прямой.
Сегмент линии имеет две конечные точки. Отрезок – это прямая линия, соединяющая две точки. Это кратчайший путь между двумя точками. Отрезок имеет определенную длину. Его длину можно измерить.
Обозначим карандашом две маленькие точки (.) как точки A и B. Соединим их, проведя прямую линию. Это формирует линейный сегмент. Отрезок линии называется двумя его конечными точками и записывается как сегмент линии AB или сегмент линии PQ.
На приведенном выше рисунке отрезок AB имеет две конечные точки A и B. Он начинается в точке A и заканчивается в точке B. Между двумя заданными точками A и B может находиться только один отрезок. Отрезок линии называется АВ. Его также можно назвать БА. Линия BA такая же, как и линия AB. Оба проходят через одни и те же две точки A и B.
Отрезок линии также может быть частью линии, как показано на рисунке ниже.
Отрезок также может быть частью луча. На рисунке ниже отрезок AB имеет две конечные точки A и B. Он является частью луча, начинающегося в точке A.
На рисунке ниже отрезок AB имеет две конечные точки A и B. Он является частью луча, начинающегося в точке A.
Параллельные прямые
Две прямые в одной плоскости либо пересекаются, либо не пересекаются. Если две прямые на плоскости встречаются, мы говорим, что две прямые пересекаются, а точка, в которой они встречаются, называется точкой пересечения. Если две прямые не пересекаются ни в одной точке, они называются параллельными прямыми. Никакие две точки не могут быть общими для двух параллельных прямых.
На рисунке выше две линии не пересекаются. Даже если мы продлим эти линии дальше, они не соприкоснутся и не встретятся друг с другом. Это параллельные линии.
Пересекающиеся линии
Давайте посмотрим на две линии AB и CD на рисунке выше. Они пересекаются в точке O. Следовательно, они не параллельны. Точка О является точкой их пересечения.
Совпадающие прямые
Три или более прямых, проходящих через одну и ту же точку на плоскости, называются совпадающими прямыми. На рисунке ниже три прямые AB, CD и EF пересекаются друг с другом в точке O.
На рисунке ниже три прямые AB, CD и EF пересекаются друг с другом в точке O.
Коллинеарные точки
Три или более точек на плоскости* называются коллинеарными, если все они лежат на одной прямой.
На рисунке выше точки A, B и C лежат на одной прямой. Следовательно, эти три точки A, B и C лежат на одной прямой.
*Плоская поверхность в геометрии называется плоскостью. Мы можем сказать, что лист бумаги из нашей тетради — это плоскость.
Измерение отрезка прямой
Линейка — инструмент, используемый в геометрии. Мы используем линейку, чтобы нарисовать отрезок. Мы также используем его для измерения длины отрезка.
Линейка обычно имеет длину 1 фут (30 см) и называется однофутовой линейкой. Иногда его просто называют масштабом. Некоторые линейки имеют длину шесть дюймов (15 см) и называются полуфутовыми линейками. Один край линейки имеет шкалу, отмеченную в дюймах, а другой край имеет шкалу, отмеченную в сантиметрах.
Прикладываем линейку ребром вдоль отрезка АВ с нулевой отметкой линейки в начальной точке А отрезка. Читаем отметку на линейке в другой конечной точке В отрезка.
На что обратить внимание
- Маленькая отмеченная точка — это точка.
- Точка не имеет ни длины, ни ширины, ни толщины.
- Точка указывает точное местоположение.
- Луч исходит из точки и уходит в бесконечность.
- У линии нет конечных точек.
- Отрезок линии имеет две конечные точки.
- Отрезок линии соединяет обе конечные точки.
- Если две линии не пересекаются ни в одной точке, они называются параллельными линиями.
- Три или более точек на одной прямой называются коллинеарными точками
- Линейка используется для рисования отрезка и измерения его длины.
Вопросы и ответы
Вопрос 1 : Начертите на бумаге две точки A и B и начертите отрезок.
Ответ : Мы отмечаем точку A на странице для письма, а затем отмечаем другую точку B на той же странице.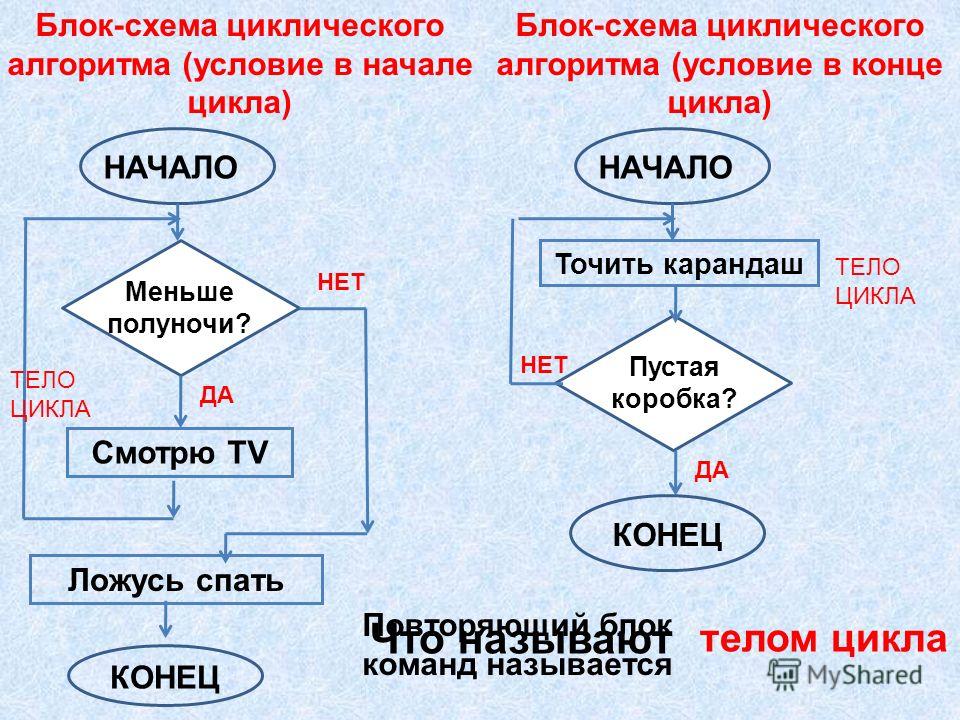 Соединяем эти две точки линией. Это сегмент линии.
Соединяем эти две точки линией. Это сегмент линии.
Вопрос 2: Нарисуйте две пересекающиеся линии.
Ответ: Берем линейку и проводим линию АВ. Затем слегка поворачиваем линейку и проводим еще одну линию CD таким образом, чтобы она проходила через какую-либо одну точку линии AB.
Вопрос 3: Напишите два основных различия между линией и отрезком линии.
Ответ:
- Отрезок имеет два конца. Линия не имеет конечной точки.
- Отрезок линии имеет определенную длину. Но линия не имеет определенной длины.
Вопрос 4: Напишите два основных отличия линии от луча.
Ответ:
- Прямая идет без конца в обоих направлениях, но луч имеет один конец и идет без конца в одном направлении.
- Линия AB совпадает с линией BA. Но луч AB отличается от луча BA.
Вопрос 5: Что означают коллинеарные точки?
Ответ: Коллинеарные точки — это точки на одной прямой. Три или более точек на плоскости называются коллинеарными, если все они лежат на одной прямой.
Три или более точек на плоскости называются коллинеарными, если все они лежат на одной прямой.
Упражнение
1. Определите рисунок ниже?
- Рэй
- Линия
- Линейный сегмент
2. Определите рисунок ниже?
- Рэй
- Линия
- Линейный сегмент
3. Определите рисунок ниже?
- Рэй
- Линия
- Линейный сегмент
4. Что из следующего имеет определенную длину?
- Рэй
- Линия
- Линейный сегмент
Верно или неверно
5. Две линии на рисунке ниже параллельны
- Верно
- Ложь
6. Две линии на рисунке ниже являются параллельными линиями
- Правда
- Ложь
Заполните пропуски
7. ………………… имеет определенную длину
- Луч
- Линия
- Сегмент линии
8.
 Но как понять через какие?
AAA
Но как понять через какие?
AAA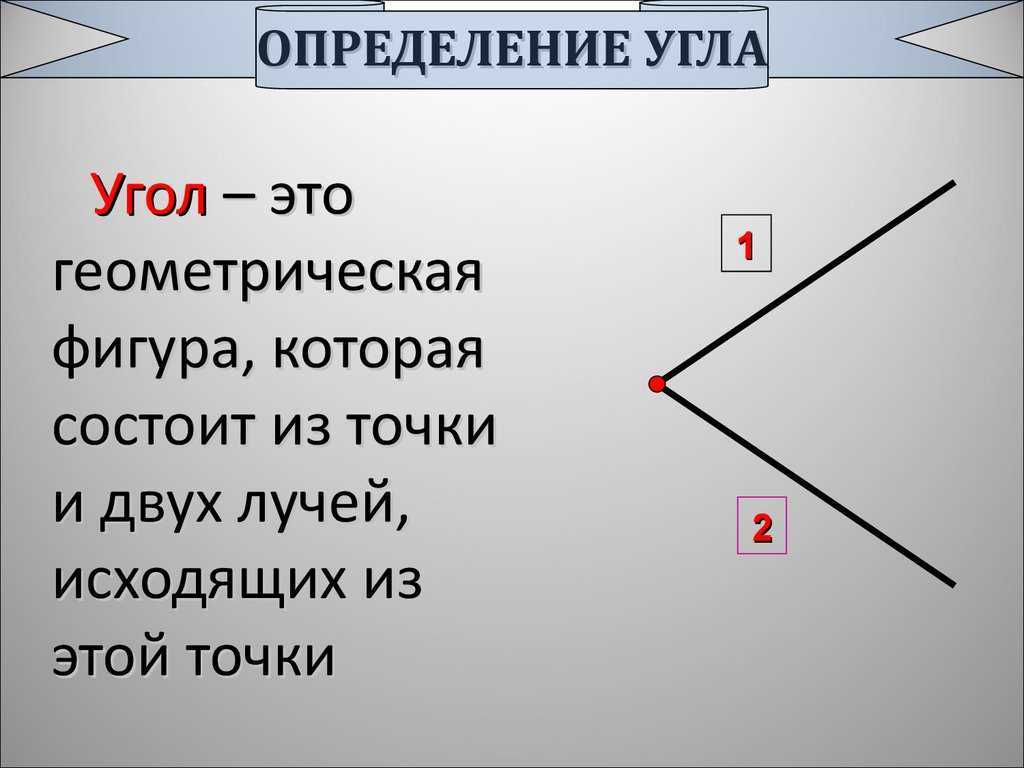 У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.