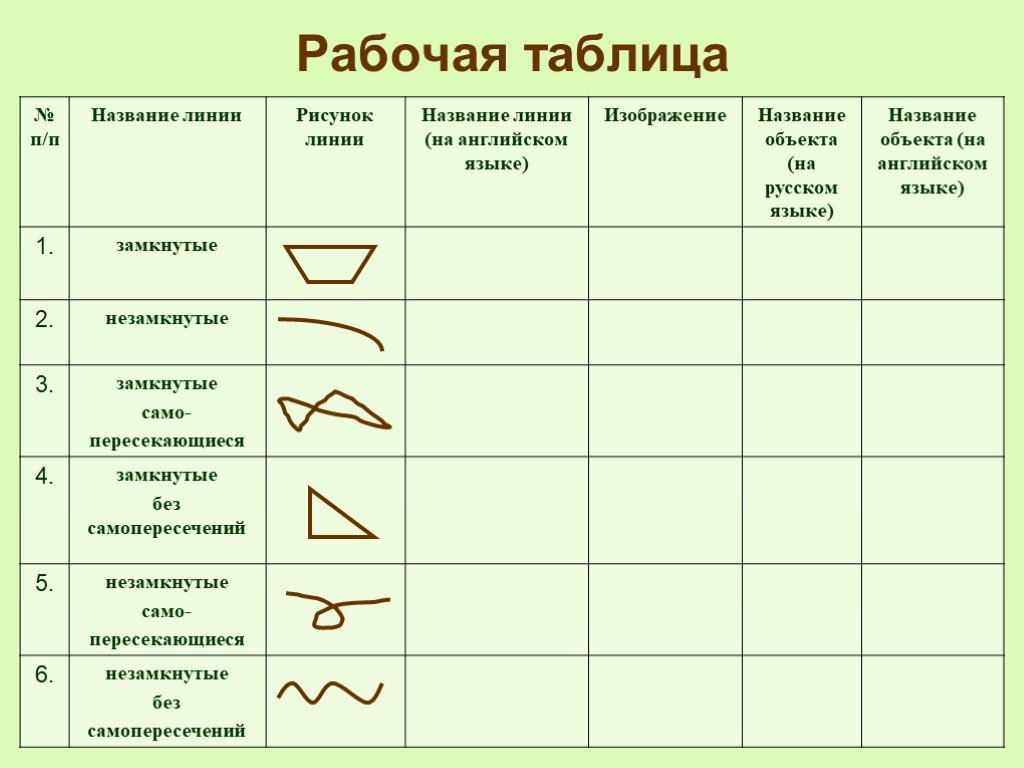
Задачи этапа | Визуальный ряд | Деятельность учителя | Деятельность учащихся | Формируемые УУД | |||||
Организационный | Создание ситуации успеха. | На ИД слайд 2,3.Приветственное слово учителя: | Учитель представляется и высказывает свое удовольствие от встречи с данным классом. | Испытывают чувство гордости за свою Родину , за свою школу и за свой класс Включаются в деловой ритм урока | Саморегуляция действий при работе в новой обстановке, с новым коллективом и новым учителем. | ||||
Рефлексия | Определить настроение на начало урока | Учитель анализирует полученную картину настроения учащихся | Учащиеся показывают карточку, которая соответствует их настроению(можно схематично зарисовать в тетрадь). | Навыки психологической рефлексии | |||||
Актуализации знаний и умений Целеполагания | Развитие эстетического восприятия учебника и его успешного освоения. Формирование представления о многообразном мире линий | На доске дата и запись «Классная работа. Разнообразный мир линий» | Предлагает детям почитать на стр.7 «Интересно».Впервые человек взял в руки кусок угля и провел им по стене пещеры еще в глубокой древности. Он изобразил контуры предметов, животных, объектов природы. Из чего состоят эти рисунки? Мы отправляемся в путешествие в разнообразный мир линий — Откройте тетради, запишите число и тему урока. | Один читает вслух -из линий Цель урока: познакомится с разными линиями и узнать как и где они применяются, как их построить. .Учащиеся делают запись в тетрадь. | Прогнозирование, рефлексия Регулятивные УУД: самостоятельное формулирование цели, планирование предстоящей деятельности. | ||||
Усвоение новых знаний и способов усвоения | Обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы: разнообразный мир линий. | На экране появляется виртуальная лаборатория «Лини», учитель рисует замкнутую и незамкнутую линии. Флеш –демонстрация 4 «ЛИНИИ» На экране интерактивная модель «Внутренняя и внешняя области» Флеш-демонстрация 2 «Внутренняя и внешняя области» Флеш-демонстрация 3 «Внутренняя и внешняя области» | Виды линий: фото (1.1) Линии можно проводить от руки , а можно с помощью различных инструментов: линейки, циркуля, лекала. Все точки одинаковы, и одна точка от другой ничем не отличаются. А мир линий разнообразен. Давайте поработаем с учебником страница 9 Линии делятся также на самопересекающиеся и линии без самопересечений Вопрос: «Что изображено на рисунке?» На рисунке 1.3 изображена замкнутая линия без самопересечений. Она делит плоскость на две области – внутреннюю и внешнюю. Сама линия служит границей этих областей. 1.Начертите в тетради замкнутую линию, закрасьте внутреннюю область синим цветом, а внешнюю – красным. 2.Чтобы из одной области попасть в другую, надо пересечь ее границу. 2.Определить сколько раз три различные кривые пересекают границу между внешней и внутренней (На столе у каждого распечататка для определения числа пересечений) Где еще встречаются внешние и внутренние области? | Упражнения из учебника №1,2. Ребята читают о происхождении слова «линия». Отвечают на вопрос №3 ст.10 учебника. Ребята рассматривают рис. Ребята рассматривают рис.1.4 Политическая карта Африки и смотрят на ИД Флеш-демонстрацию 3 «Внутренняя и внешняя области» Ответы: граница озера, море, граница государства и т.д. Ребята выполняют упражнение Рассматривают рисунок и подсчитывают количество точек пересечений. Приводят примеры | Познавательные УУД: анализ данных, постоение линий и их конструкций, распознавание различных линий , проводение наблюдений и экспериментов под руководством учителя, формирование математической речи. Регулятивные УУД: развитие внимания, сохранение цели и четкое выполнение требований познавательной задачи. | ||||
Физминутка | Учитель показывает несколько физических упражнений | Повторяют за учителем | Здоровьесбережение, саморегуляция | ||||||
Выполняем упражнения из У. Посетили одно большое государство. Какие наши новые знакомые? | Ребята выполняют в тетради, один человек комментирует решение с места. КРИВЫЕ линии. Перечисляют. | Познавательные:Поиск и выделение необходимой информации, которая определяет данную предметную область, применение ее при выполнении практических заданий | |||||||
Творческого применения и добывания знаний в новой ситуации (проблемные задания) | Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков. | Клетчатая бумага – это удобный «инструмент» для вычерчивания линий; он помогает видеть характерные точки линии, выработать алгоритм изображения. Рисуем на клетчатой бумаге упр. Учебник №10 на воспроизведение рисунка всегда нужно начинать с анализа, который лучше выполнять с карандашом в руке. | Учащиеся выполняют задание(помощь учителя при необходимости) | Позитивное отношение к учебному процессу, творческий подход к решению задач, умения эмоционального общения Осознание роли приобретенных знаний и способов решения практических задач с помощью моделирования | |||||
Подведение итогов урока | Дать качественную оценку работы класса и отдельных обучаемых | Предлагается учащимся подвести итоги (стр.9 по вопросам и заданиям) Обобщить знания и умения пот слайду | Отвечают на вопросы и выполняют задания -Сообщают, чему научились, что узнали на уроке | Осознание роли приобретенных знаний и способов решения практических задач с помощью моделирования различных линий. Контроль и оценка процесса и результата деятельности, выделение и осознание учащимися того, что уже усвоено. Сопоставление внешней оценки учителя и самооценки. Сопоставление и сравнение личных успехов с успехами других. | |||||
Рефлексия | Сформировать рефлексивную самооценку деятельности на уроке | Просьба учителя нарисовать в тетрадь рисунок из слайда, который соответствует настроению учащегося в конце урока | Дети рисуют значок в тетради | Навыки психологической рефлексии, умение выражать настроение, анализировать его в течение урока. | |||||
Информирования о домашней работе | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания | Учитель комментирует домашнее задание по тексту учебника и отвечает на вопросы учащихся. | Задают вопросы при непонимании. Записывают задание в дневники | Формирование регулятивного опыта. Развитие умений формулировать вопросы. | |||||
(рис.1.2)
1.2
№6
Спираль (№10) можно «прочитать»: одна клетка вправо, одна клетка вверх, две клетки влево, и т.д.; теперь легко будет ее воспроизвести. Сначала это нужно сделать «от руки», тонко очерченным простым карандашом, а потом при желании провести ярче уже намеченные линии с помощью линейки. (Можно все делать «от руки», без инструментов).
Конспект урока: «Разнообразный мир линий».
2.09.2015г. Тема: «Разнообразный мир линий»
Тип урока : Усвоение новых знаний
Цели урока: -познакомить учащихся с разнообразным миром линий; показать отличия замкнутой линии от незамкнутой линии, линии самопересекающейся от линий не имеющей самопересечений; уметь различать линии на рисунках и чертежах; иметь представления о внутренней и внешней областях линий. -развивать представления о линии, продолжить формирование графических навыков и измерительных умений, развивать внимание, пространственное мышление, умение анализировать, сравнивать, творческие способности учащихся, поддержание интереса к предмету. —воспитание аккуратности, культуры общения, воспитание потребности к самообразованию, умение организовать свою работу и поэтапное её выполнение, воспитание трудолюбия, интереса к предмету при помощи интересного геометрического и наглядного материала.
УУД: -Личностные : формировать устойчивую мотивацию к изучению и закреплению учебного материала; — Регулятивные: осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач; прилагать волевые усилия. Коммуникативные: учить строить высказывания, аргументировано доказывать свою точку зрения; формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы.
Планируемый результат:
Предметные: различать линии на рисунках и чертежах. Личностные: Иметь первоначальное представление о линиях, выражают интерес к изучению предметного курса; проявляют готовность и способность к саморазвитию; имеют мотивацию к обучению и познанию. Метапредметные : Уметь планировать пути достижения целей; устанавливать целевые приоритеты; осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач; прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей.
(Регулятивные УУД). Уметь формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром; (Коммуникативные УУД)
Формируемые УУД
1.Мотивация к учебной деятельности.
-настроить учащихся на активную работу на уроке;
-включить учащихся в учебную деятельность;
-создать положительный эмоциональный настрой на урок.
Здравствуйте, ребята! Я рада приветствовать вас на нашем уроке, где вы вспомните много нового и интересного. На уроке вы должны быть внимательными и усидчивыми. Кто готов к работе? Сядьте красиво и удобно.
Эпиграф к сегодняшнему уроку
Математику нельзя
Изучать, наблюдая,
как это делает сосед!
А. Ниве
Учащиеся садятся
Личностные:
Выражение положительного отношения к процессу познания
2.
Устный счёт.
Игра: «Цепочка»
-отрабатывать вычислительные навыки
-включить учащихся в учебную деятельность;
-создать положительный эмоциональный настрой на урок.
-воспитывать интерес к выполняемой работе
Откроем учебник на стр.9 №12 ; №13 устно по цепочке
Учащиеся считают
Предметные: Совершенствуют навыки сложения, вычитания, умножения и деления
Коммуникативные: формируют навыки учебного сотрудничества Регулятивные: оценивают правильность выполнения действия; участвуют в диалогах Личностные Выражение положительного отношения к процессу познания
3.Постановка темы и задач урока
— развивать логическое мышление, математическую речь
В белом поле по дороге
мчится конь мой одноногий
и на много-много лет
оставляет он свой след.
-Какие же следы может оставить карандаш?
-Все точки одинаковы, а вот мир линий более разнообразен.
-Как вы думаете, о чём мы сегодня будем говорить?
— Значит, какая тема нашего урока?
-Сформулируйте цели и задачи на сегодняшний урок.
-Карандаш
-точки, лини
— О различных линиях.
-Разнообразный мир линий.
-Узнать разнообразии видов линий
-учиться различать виды линий на чертежах и рисунках
Коммуникативные:
уметь с помощью вопросов добывать недостающую информацию.
Регулятивные: ставить учебную задачу на основе соотнесения того, что уже известно и усвоено, и того, что еще неизвестно; самостоятельно формулировать познавательную цель и строить действия в соответствии с ней.
Личностные
Выражение положительного отношения к процессу познания
4. Систематизация знаний. (Изучение нового материала)
-показать какие существуют виды линий; учить отличия замкнутую линию от незамкнутой, линии самопересекающейся от линий не имеющей самопересечений; иметь представления о внутренней и внешней областях линий.
Учить различать линии на рисунках и чертежах
-Ребята, а как получаются линии?
-Слово линия происходит от латинского слова linea, означающего «лен, льняная нить, шнур, веревка». Возьмем в руки нить и выложим на плоскости стола произвольную линию. У вас получилось?
-Можно ли из проволочки соорудить линию?
А теперь взгляните на слайд. (Учащимся предлагаются задания на распознавание линий)
-Чем отличаются линии одной группы от другой?
— Какие два вида линий вы теперь знаете?
Выложите из нити:
— замкнутую линию ( 1 вариант),
— незамкнутую линию (2 вариант)
-У вас получилось справиться с заданием?
-Давайте откроем учебник, стр. 5, рис. 1.1, изображены линии. Выберите из них и назовите номер:
1. Замкнутые линии.
2. Незамкнутые
— Обратите внимание на линию под №5
-Что вы можете о ней сказать?
-значит существует ещё один вид линий?
-Какой?
Давайте посмотрим стр 6 , рис. 1.2
1.Замкнутые не самопересекающаяся линии.
2. Замкнутые самопересекающаяся линии.
2. Незамкнутые не самопересекающаяся
3. Самопересекающаяся
-Ребята обратите внимание на №1 , №3 рис.1.2. Линии такого вида , то есть все замкнутые линии без самопересечения, делят плоскость на две области : внутреннюю и внешнюю. Сама линия в этом случае является границей. Посмотрите слайд.
-что нового вы сегодня узнали?
-С какими видами линий познакомились?
-На какие области замкнутая линия делит плоскость?
-Поднимите руки кто действительно разjбрался с видами линий?
-Встаньте , кто не понял как определить вид линий.
Линия — множество точек
Да
Да
В первой группе линии не замкнутые , а во второй замкнутые.
Замкнутые, незамкнутые
Да
2, 5, 6.
1, 3, 4.
-Что она самопересекается (Лысенко Алина)
-Да
-Самопересекающаяся
1, 3
5, 7, 8, 9.
4.
2, 6.
-Какие виды линий существуют
-Замкнутые, незамкнутые, самопересекающиеся
-Внутреннюю и внешнюю.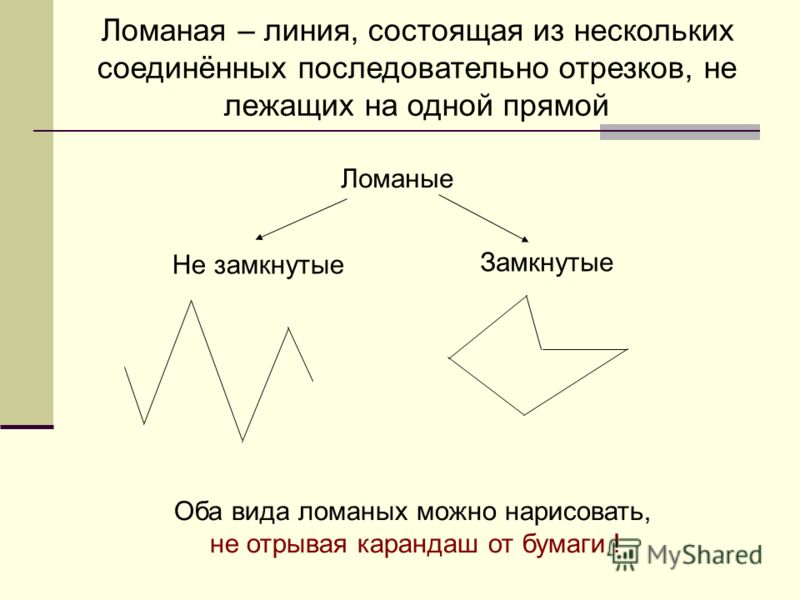
Предметные: различать линии на рисунках и чертежах.
Личностные: Иметь первоначальное представление о линиях, выражают интерес к изучению предметного курса; проявляют готовность и способность к саморазвитию; имеют мотивацию к обучению и познанию. Метапредметные : Уметь планировать пути достижения целей; устанавливать целевые приоритеты; осуществлять познавательную рефлексию в отношении действий по решению учебных и познавательных задач; прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей. Регулятивные: Уметь формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности; задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром;
5. Актулизация знаний
-отрабатывать приобретённые знания
-развивать логическое мышление, математическую речь
-воспитывать интерес к выполняемой работе
На стр 6 выполним задание №2 устно.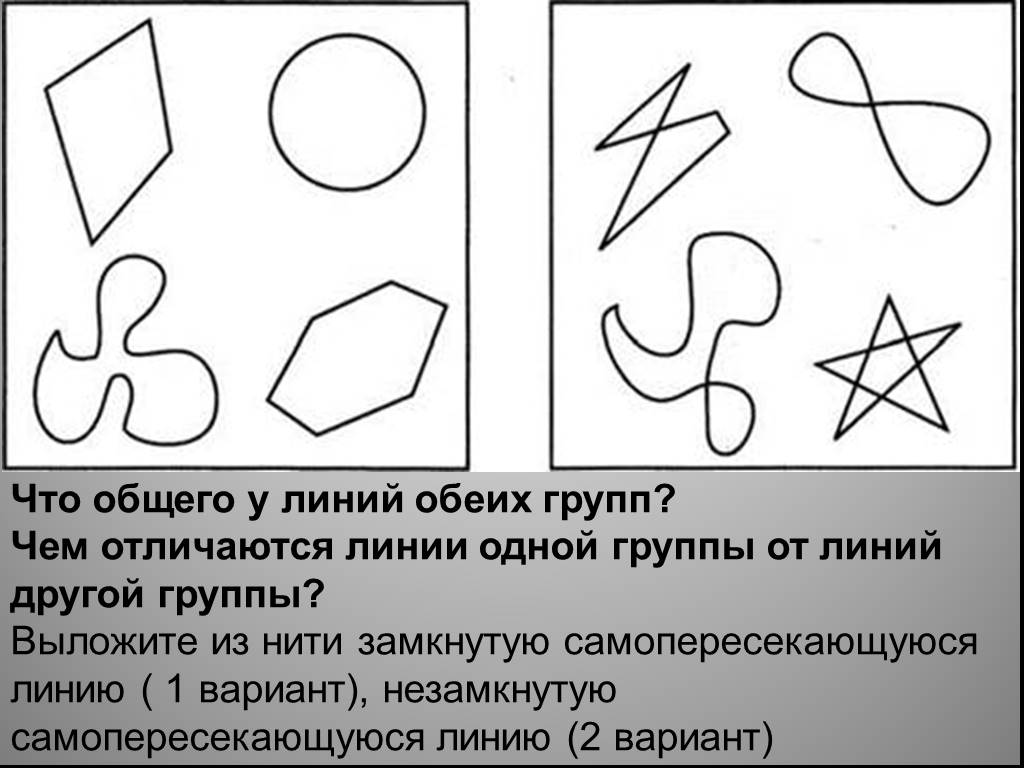
Стр.7 №4
Стр.7 №6 выполняем в тетради работая в парах
-Нет нельзя, потому что через две точки можно провести только одну прямую (Шавульский Максим)
-Замкнутую, самопересекающуюся линию (Клёван Иван)
Поменяйтесь тетрадями и оцените работу друг друга.
Предметные: Совершенствуют умения определять виды линий . Закрепляют понятия: внутренняя и внешняя область
Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
Регулятивные: оценивают правильность выполнения действия; участвуют в диалогах;
Познавательные: проводить анализ способов решения задач
6. Физ. минутка
-создать положительный эмоциональный настрой на урок.
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
А теперь тихонько сесть.
Делают зарядку
Личностные
Выражение положительного отношения к процессу познания
7. Математически диктант.
-проверить качество усвоения нового материала, умение определять виды линий
Математический диктант
1. Запишите, какие из линий являются замкнутыми?
2. Запишите, какие из линий являются незамкнутыми с самопересечениями?
3. На рисунке дана замкнутая линия. Найдите:
А) точки, принадлежащие внешней области линии;
Б) точки, принадлежащие внутренней области линии.
4. Выберите неверные утверждения:
А) данная линия незамкнута;
Б) данная линия имеет 4 самопересечения;
В) данная линия замкнута;
Г) данная линия не имеет самопересечений.
Задачи на изображение линий:
1. Нарисуйте замкнутую линию в тремя самопересечениями.
2. Нарисуйте незамкнутую линию с двумя самопересечениями.
—
Работают самостоятельно в тетрадях
Предметные: Совершенствуют умения определять виды линий. Закрепляют понятия: Внешняя и внутренняя область
Коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
Регулятивные: оценивают правильность выполнения действия; участвуют в диалогах;
Познавательные: проводить анализ способов решения задач
8. Итог урока. Рефлексия.
-учить делать выводы, объективно оценивать свою деятельность
Над какой темой работали на уроке?
– Что выполняли на уроке? Какие задания вызвали у вас затруднения? Почему? Что помогло выполнить задания?
– Что хотелось бы еще узнать?
– Как оцениваете свою работу на уроке?
– Какие виды линий вы теперь знаете?
Личностные:
Выражение положительного отношения к процессу познания
9.
Домашнее задание
-отрабатывать навыки и умения.
П.1.1. № 9; №10
Предметные: Совершенствуют умения определять виды линий. Закрепляют понятия: Внешняя и внутренняя область
Перпендикулярные линии в реальной жизни|Параллельные линии в реальной жизни
Содержание
| 1. | Введение |
| 2. | Параллельные линии |
| 3. | Наклонные линии |
| 4. | Перпендикулярные линии |
| 5. | Параллельные линии в реальной жизни |
| 6. | Перпендикулярные линии в реальной жизни |
| 7. | Отношение эквивалентности |
| 8. | Резюме |
| 9. | Часто задаваемые вопросы |
29 октября 2020 г.
Время прочтения: 5 минут
Введение
просматривая этот блог, я уверяю вас, что ваше восприятие этих строк изменится.
Параллельные линии
Параллельные линии — это не что иное, как линии на плоскости, которые не пересекаются.
Мы также можем сказать, что параллельные линии — это прямые линии на плоскости, которые не пересекаются ни в одной общей точке.
Проще говоря, для простоты понимания, я бы сказал, что «Прямые на плоскости, которые не пересекаются друг с другом, одновременно не имеют общей точки», называются параллельными.
Наклонные линии
Эти линии существуют в двух измерениях и трех измерениях геометрии. В трехмерной геометрии мы сталкиваемся с новой линией — «косыми линиями». Эти линии не что иное, как две линии, но они не пересекаются и не параллельны.
Основное различие между параллельными и косыми линиями состоит в том, что первые лежат в одной плоскости, а вторые — в разных плоскостях.
Интересные факты о параллельных прямых
Математически интересные факты можно назвать свойствами.
Давайте посмотрим на некоторые из них.
- Параллельные линии всегда равноудалены друг от друга.
- Они не пересекаются ни в одной точке.
- Их можно неограниченно расширять в обоих направлениях.
- Параллельные линии являются копланарными линиями.
- Если m 1 и m 2 являются наклонами двух прямых, если они параллельны, мы говорим
\[m_1 = m_2\]
Перпендикулярные прямые
Две различные прямые, пересекающиеся друг с другом под прямым углом, называются перпендикулярными прямыми. Эти линии касаются друг друга в одной точке.
В младших классах мы проходили элементарную геометрию, где перпендикулярные линии означают отношения между двумя линиями, которые встречаются в одной точке, а точка — под прямым углом к другой.
Интересные факты о перпендикулярных прямых
- Эта линия всегда пересекается под прямым углом.
- Если две прямые перпендикулярны одной прямой, то они параллельны и никогда не пересекутся.
- Перпендикулярные прямые всегда пересекаются, но обратное неверно; то есть мы не можем сказать, что пересекающиеся линии всегда перпендикулярны.
- Если две линии перпендикулярно представляют наклон, то
\[m_1 \times m_2 = -1.\]
Параллельные линии в реальной жизни
Сначала рассмотрим практический пример. Возьмем два города
Дели и Бхопал. Вероятность того, что эти два города встретятся друг с другом, равна нулю.
У них нет точки соприкосновения.
В реальной жизни мы видим параллельные линии в:
- Железнодорожных путях
- Четырехполосные, шестиполосные дороги
- Противоположные стороны школьной и белой доски
- Противоположные стены или двери в помещении
- Постановка в очередь
Железнодорожный путь с параллельными линиями
Перпендикулярные линии в реальной жизни
Ниже приведены примеры перпендикулярных линий в реальной жизни:
- Футбольное поле
- Железнодорожный переезд
- Аптечка первой помощи
- Строительство дома, в котором пол и стена перпендикулярны
- Телевидение
- Дизайн в окнах
Телевидение с перпендикулярными краями
Отношение эквивалентности
Существует отношение эквивалентности, которое связывает параллельность и перпендикулярность, которое определяется рефлексивностью, симметричностью и транзитивностью.
Возьмем трех друзей A, B и C
Рефлексивно
Любой друг является другом самому себе, что известно как рефлексивность, что является простым фактом: я всегда люблю себя; это фундаментальная психология.
Симметричный
Возьмем двух друзей A и B, если A является другом B, то B является другом A, что обозначается перпендикулярностью, то есть A перпендикулярно B и B перпендикулярно A. Они встречаются друг друга в общей точке.
Переходный
Возьмем трех друзей A, B и C. Трое являются друзьями друг друга, которые мы можем соотнести с параллельными линиями, то есть A является другом B, B является другом A и B другом C и От С до А, которые хорошо можно представить тремя параллельными линиями, стоящими одна за другой, не пересекающимися и не встречающимися друг с другом, а встречающимися в практической жизни через онлайн-режим через Skype, Zoom по новейшим технологиям.
Если выполняются три условия, это называется отношением эквивалентности.
Резюме
Параллельные и перпендикулярные линии находят свое применение в обширной области. Хотя мы узнали несколько, читатель должен исследовать больше вещей в этом направлении, что было бы более интересным для них, чтобы двигаться дальше. Эти линии помогают многим людям выполнять свою деятельность в повседневной жизни.
Часто задаваемые вопросы (FAQ)
Параллельные линии пересекаются?
Нет параллельных линий, которые не пересекаются и не встречаются.
Что такое перпендикулярные линии?
Две прямые, пересекающиеся друг с другом под прямым углом, называются перпендикулярными прямыми.
Под какими углами пересекаются перпендикулярные прямые?
Перпендикулярные прямые пересекаются под углом 90°.
Какие есть примеры параллельных прямых в реальной жизни?
В реальной жизни железнодорожные пути, разметка на улицах, края тротуаров, коробка цветных карандашей, аккуратно расставленных одна за другой — вот несколько примеров параллельных линий.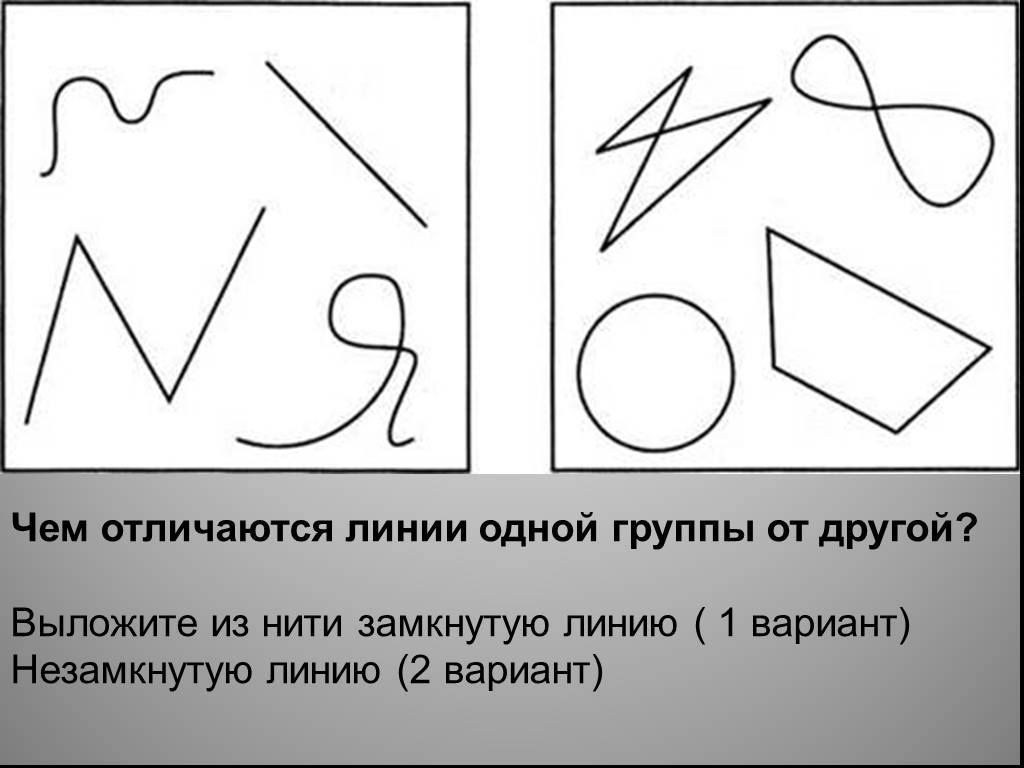
Какие есть примеры перпендикулярных линий в реальной жизни?
Железнодорожный переезд, символ аптечки, футбольное поле, телевизор и т. д.
5 удивительных способов увидеть математику в мире
Вы когда-нибудь останавливались, чтобы оглянуться вокруг и заметить все удивительные формы и узоры, которые мы видим в мире? вокруг нас? Математика формирует строительные блоки мира природы, и ее можно увидеть потрясающим образом. Вот несколько из моих любимых примеров математики в природе , но есть и много других примеров.
Последовательность Фибоначчи:
Названная в честь знаменитого математика Леонардо Фибоначчи, эта числовая последовательность представляет собой простой, но глубокий узор.
На основе «задачи о кролике» Фибоначчи эта последовательность начинается с чисел 1 и 1, а затем каждое последующее число находится путем сложения двух предыдущих чисел. Следовательно, после 1 и 1 следует число 2 (1+1).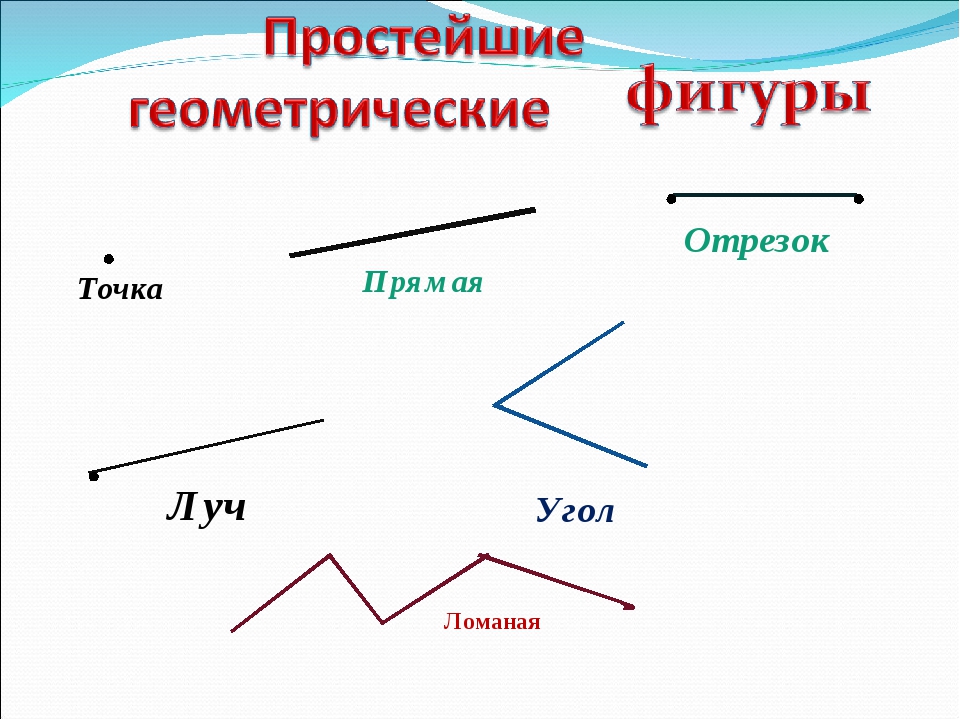
Следующее число 3 (1+2), затем 5 (2+3) и так далее.
Что примечательно, так это то, что числа в последовательности часто встречаются в природе .
Несколько примеров включают количество спиралей в сосновой шишке, ананасе или семенах подсолнуха или количество лепестков на цветке.
Числа в этой последовательности также образуют уникальную форму, известную как спираль Фибоначчи, которую мы снова видим в природе в виде раковин и в форме ураганов.
Фракталы в природе:
Фракталы — еще одна интригующая математическая форма, которую мы видели в природе. Фрактал — это самоподобная, повторяющаяся форма, то есть одна и та же базовая форма снова и снова видна в самой форме.
Другими словами, если вы увеличите или уменьшите масштаб, везде будет видна одна и та же форма.
Фракталы составляют многие аспекты нашего мира, включая листья папоротников, ветви деревьев, разветвления нейронов в нашем мозгу и береговые линии.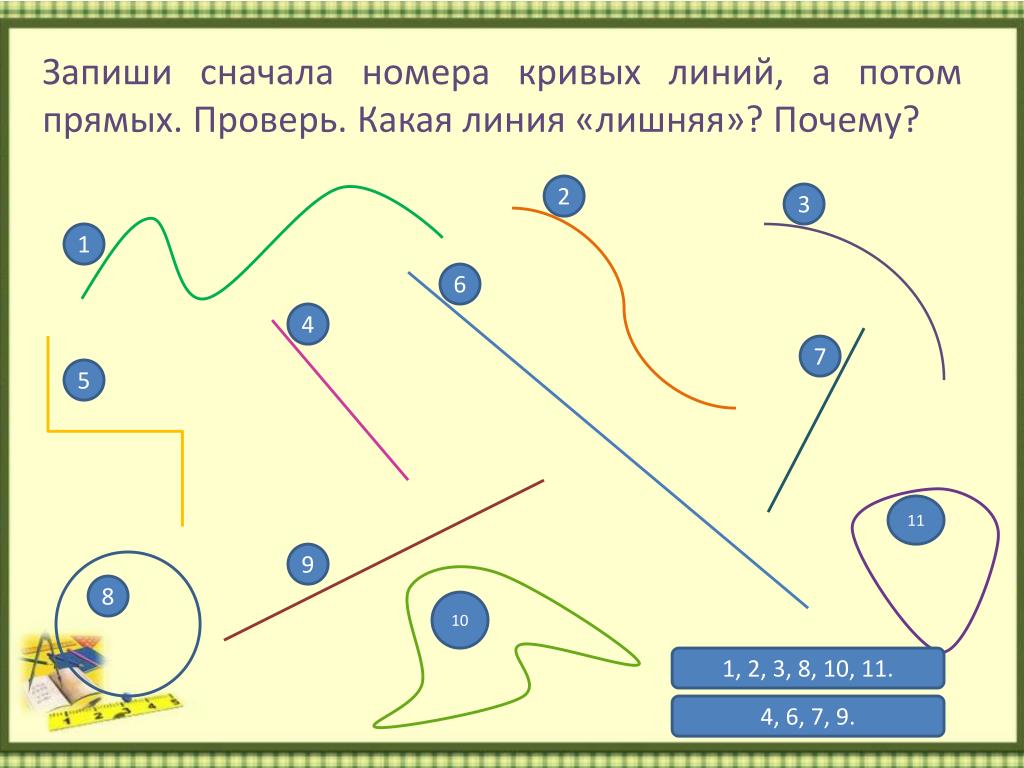
Узнайте больше о фракталах и о том, как мы видим и применяем их в современном мире, в Fractal Foundation.
Шестиугольники в природе:
Еще одно геометрическое чудо природы — шестиугольник. Правильный шестиугольник имеет 6 сторон одинаковой длины, и эта форма снова и снова встречается в окружающем нас мире.
Самый распространенный пример использования шестиугольников в природе — пчелиный улей.
Пчелы строят улей, используя мозаику из шестиугольников. Но знаете ли вы, что каждая снежинка также имеет форму шестиугольника?
Мы также видим шестиугольники в пузырях, которые составляют пузырь плота. Хотя мы обычно думаем о пузырьках как о круглых, когда многие пузырьки сталкиваются друг с другом на поверхности воды, они принимают форму шестиугольников.
Концентрические круги в природе:
Другая распространенная форма в природе — набор концентрических кругов. Концентричность означает, что все круги имеют один и тот же центр, но разные радиусы.
Это означает, что все круги разных размеров, один внутри другого.
Типичным примером является рябь пруда, когда что-то ударяется о поверхность воды. Но мы также видим концентрические круги в слоях лука и кольцах деревьев, которые формируются по мере его роста и старения.
Если вы живете рядом с лесом, вы можете поискать упавшее дерево, чтобы сосчитать кольца, или поискать паутину-шар, которая состоит из почти идеальных концентрических кругов.
Математика в космосе:
Удаляясь от планеты Земля, мы также можем увидеть многие из этих же математических особенностей в космосе.
Например, наша галактика имеет форму спирали Фибоначчи. Планеты вращаются вокруг Солнца по концентрическим траекториям. Мы также видим концентрические круги в кольцах Сатурна.
Но мы также видим уникальную симметрию в космическом пространстве, которая уникальна (насколько могут сказать ученые), и это симметрия между Землей, Луной и Солнцем, которая делает возможным солнечное затмение.
Каждые два года Луна проходит между Солнцем и Землей таким образом, что кажется, что она полностью закрывает Солнце. Но как это возможно, если Луна намного меньше Солнца?
Из-за математики.
Видите ли, Луна примерно в 400 раз меньше Солнца, но и примерно в 400 раз дальше.
Эта симметрия допускает полное солнечное затмение, которого не бывает ни на одной другой планете.
Разве природа не прекрасна??
Хотите узнать еще больше об этих темах и глубже изучить их со своими детьми? Попробуйте мою дополнительную программу по математике: Математика в природе.
Посмотрите, что ваши дети изучат в этом коротком видео:
Эта учебная программа, разработанная для классов 3-6 , предлагает практические уроки, чтобы посмотреть на математику в реальном мире, а также отработать важные математические навыки.
Он включает в себя списка иллюстрированных книг по каждой теме, подробное руководство для учителя , раздаточных материала для учащихся для уроков, сводных страниц с занимательными фактами и список из проектов по математике и искусству , чтобы сопровождать каждый тема.