Содержание
Презентация призма — Математика — Презентации
Понятие призмы
Многогранник , составленный из двух равных многоугольников A 1 A 2 …A n и B 1 B 2 …B n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой
В 5
В 4
В 1
В 3
В 2
A 5
A 4
A 1
A 3
A 2
Многоугольники A 1 A 2 …A n и B 1 B 2 …B n называются основаниями призмы
В 5
В 4
В 1
В 3
В 2
В 5
В 4
A 5
A 4
В 1
В 3
A 1
A 3
В 2
A 2
A 5
A 4
A 1
A 3
а параллелограммы – боковыми гранями призмы
A 2
В 5
В 4
Отрезки A 1 B 1 , A 2 B 2 , … , A n B n называются боковыми ребрами призмы
В 1
В 3
В 2
Боковые ребра призмы равны и параллельны
A 5
A 4
В 5
В 4
A 1
A 3
В 1
В 3
A 2
В 2
A 5
Вершины многоугольников A 1 , A 2 , … , A n и B 1 , B 2 , … , B n называются вершинами призмы
A 4
A 1
A 3
A 2
Высота призмы
В 5
В 4
В 1
В 3
В 1 Н ⊥ (А 1 А 2 А 3 )
В 2
В 3 К ⊥ (А 1 А 2 А 3 )
A 5
A 4
A 3
A 1
К
Н
A 2
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы
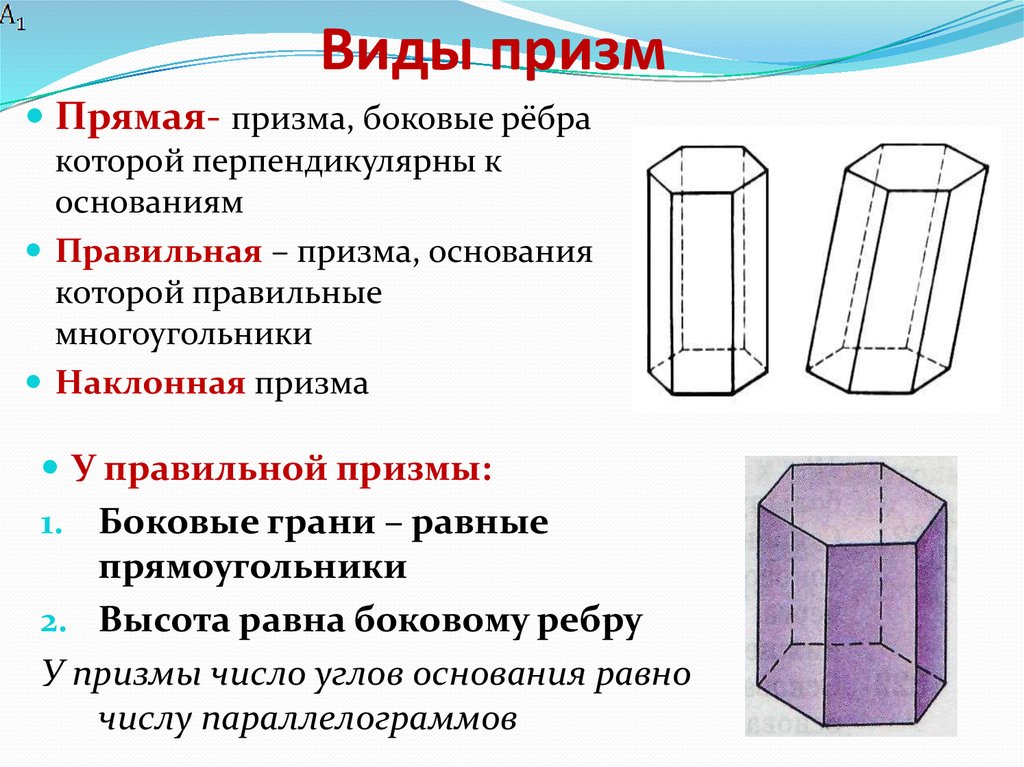
Виды призм
Прямая
Наклонная
В 4
В 5
В 5
В 4
В 1
В 3
В 3
В 1
В 2
В 2
A 5
A 4
A 4
A 5
A 1
A 3
A 1
A 3
A 2
A 2
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой , высота – боковое ребро
в противном случае – наклонной .
Правильная призма
В 4
В 5
В 3
В 1
В 2
A 5
A 4
A 3
A 1
A 2
Прямая призма называется правильной , если её основания – правильные многоугольники
У правильной призмы все боковые грани – равные прямоугольники
Правильные призмы
Площадь поверхности призмы
S полн. = S бок. + 2 S осн.
Площадью боковой поверхности призмы называется сумма площадей её боковых граней
Площадью полной поверхности призмы называется сумма площадей всех её граней
Теорема о площади боковой поверхности прямой призмы
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы
S бок. = Р осн. · h
= Р осн. · h
Доказательство.
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте h призмы.
S бок. = A 1 A 2 · h + A 2 A 3 · h + A 3 A 4 · h + … + A n-1 A n · h =
= (A 1 A 2 + A 2 A 3 + A 3 A 4 + … + A n-1 A n ) · h = P осн. · h
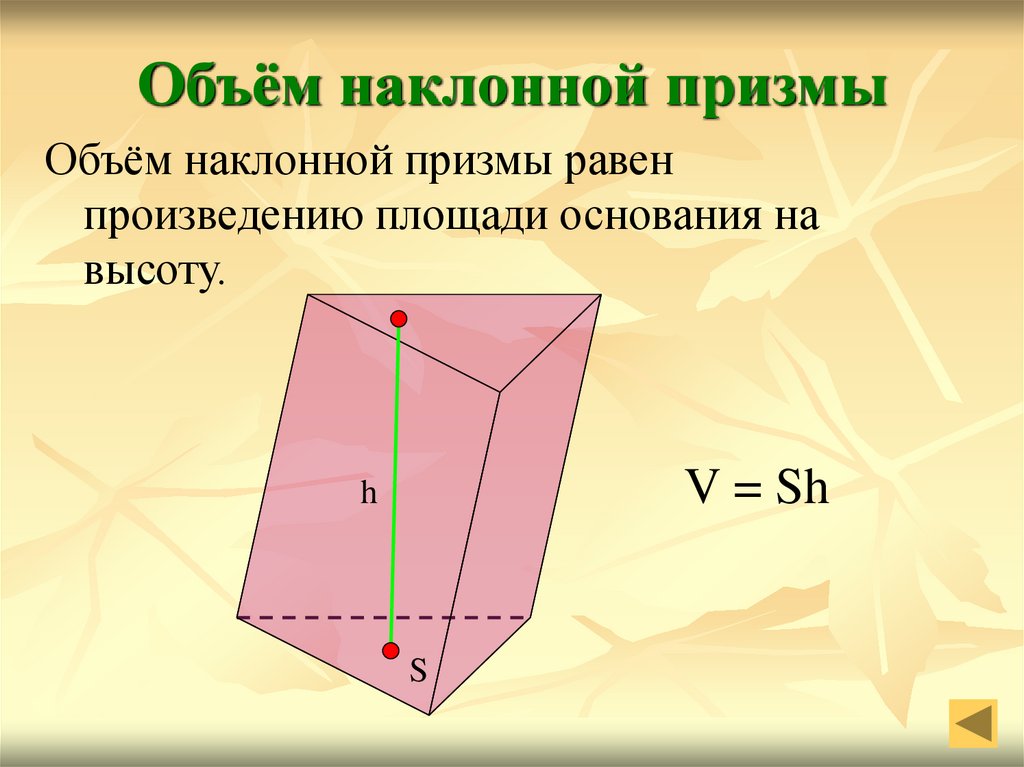
Объем призмы
Объем призмы равен произведению площади основания на высоту призмы.
В 5
В 4
V призмы = S осн. · h
В 3
В 1
В 2
A 5
A 4
A 1
A 3
A 2
В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет на составляющие и получить спектр, он использовал трехгранную стеклянную призму.
Чтобы разложить свет на составляющие и получить спектр, он использовал трехгранную стеклянную призму.
Ученый обнаружил, что, собрав раздробленный луч с помощью второй призмы, можно опять получить белый свет. Так он доказал, что белый свет является смесью разных цветов. Проходя через призму, световые лучи преломляются.
«Я затемнил мою комнату, − писал он, − и сделал очень маленькое отверстие в ставне для пропуска солнечного света».
На пути солнечного луча ученый поставил особое трехгранное стеклышко – призму. На противоположной стене он увидел разноцветную полоску – спектр. Ньютон объяснил это тем, что призма разложила белый цвет на составляющие его цвета. Ньютон первый разгадал, что солнечный луч многоцветный.
Но лучи разного цвета преломляются в разной степени – красный в наименьшей, фиолетовый в наибольшей. Именно поэтому, проходя через призму, белый цвет дробится на составные цвета.
Преломление света называется рефракцией, а разложение белого света на разные цвета – дисперсией.
Применение призм в лечении косоглазия
Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное время положительных сферо – призматических элементов различной сферической и призматической диоптрийности.
Графически это выглядит следующим образом:
Объем прямой призмы — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Урок геометрии в 11 классе
Учитель математики Манджиева Н.И.
МБОУ «Зултурганская СОШ
2012-2013 уч. год
а)
б)
в)
г)
д)
Какой многогранник называется призмой?
Какая призма называется прямым?
Какая призма называется правильной?
Что является основанием правильной
треугольной призмы?
Чем являются боковые грани призмы?
Прямой призмы? Правильной призмы?
3. Выберите неверное утверждение
а) За единицу измерения объемов
принимается куб, ребро которого равно
единице измерения отрезков;
б) тела, имеющие равные объемы, равны;
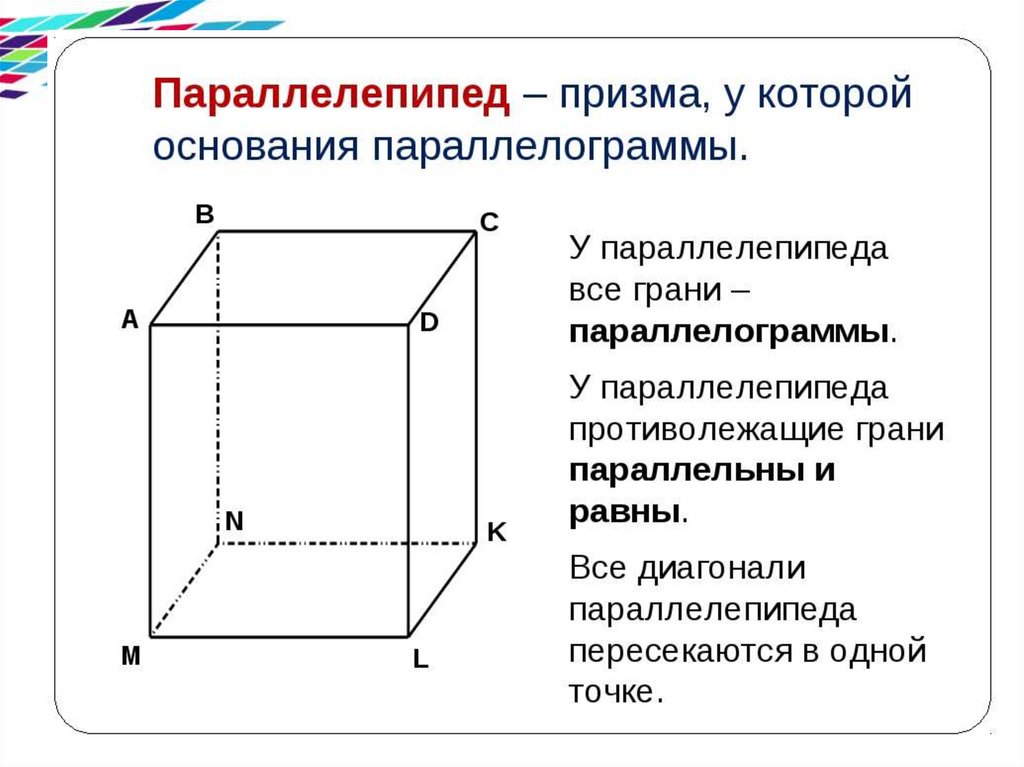
в) объем прямоугольного параллелепипеда
равен произведению трех его измерений;
г) объем куба равен кубу его ребра;
д) объем прямоугольного параллелепипеда
равен произведению площади основания на
высоту.
е) Сформулируйте свойства объемов?
.
Как вычислить объем прямоугольного
параллелепипеда?
Найдите объем прямоугольного
параллелепипеда, если его длина равна 6
см, ширина — 7 см, а диагональ — 11 см.
а) 252 см3; б) 126 см3; в) 164 см3;
г) 462 см3; д) 294 см3.
Измерения прямоугольного параллелепипеда
равны 3 см, 18 см, 4 см. Найти ребро куба
объем которого равен объему
данного параллелепипеда
4 см
3 см
? см
18 см
Vпар-да = Vкуба
Сформулируйте следствие из
теоремы об объеме
прямоугольного параллелепипеда,
в основании которого
прямоугольный треугольник.
Теорема. Объём прямой
призмы равен
произведению площади
основания на высоту.
I часть
Дано: ABCA1B1C1 –
прямая призма.
B1
A1
Доказать: V = Sосн ·h
D1
C1
B
A
D
Доказательство.
Проведем высоту BD, которая
делит ∆АВС на два
прямоугольных треугольника и
плоскость (BDD1)┴ (ABC)
C
Получим две призмы, основания которых прямоугольные
треугольники, и они прямые, для вычисления объёма
применим следствие 2.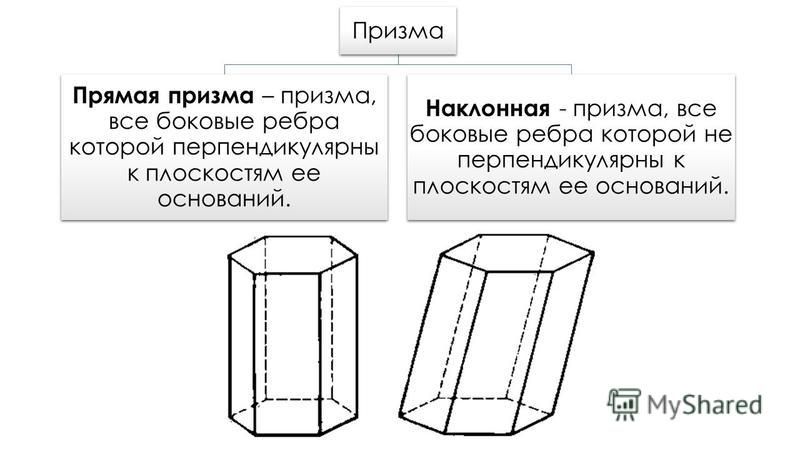
V1 и V2 их объемы V1 = SABD ·h, V2 = SDBC ·h,
тогда V= V1 + V2 = SABD ·h + SDBC ·h =h · (SABD+
SDBC) = h · SABC = Sосн ·h
II часть
Рассмотрим n-угольную
произвольную призму. Ее
можно разбить на (n -2)
прямые призмы (рис. 1). Объём
каждой треугольной призмы
можно вычислить применяя
I часть теоремы
S3
S1
(рис. 1)
S2
V= V1+V2+ V3+…+ Vn-2
=S1 ·h +S2 ·h+S3 ·h+…+
Sn-2 ·h = h · (S1 + S2 +S3
+…+Sn-2 ) = Sосн ·h
Т. о. V= Sосн ·h
C1
B1
C
45°
B
A1 В основании прямой призмы лежит
прямоугольный равнобедренный
треугольник
АВС.
Дано:
ABCA
6 см
1B1C1- прямая призма,
∠АСВ
=90°,
АС=СВ, BN=NA,
точка N делит
AC=BC,
∠АВС=90°,
гипотенузу
∠CNC1= 45°,пополам.
СС1=6 см.
ОтрезокVС1N составляет угол 45° с
A Найти:
плоскостью основания.
N
Боковое ребро равно 6 см.
Решение.
V= Sосн ·h
Найти объём призмы.
S ABC
1
a b
2
CN=CC1=6 cм
1
2
2
3
CN
V
(
6
2
)
6
6
6
216
см
CB
6 2см
2
cos 45
Ответ: 216 см3
B1
C1
Основанием прямой призмы
является ромб, острый угол
A1
D1
ABCDA
1B1C1D1- прямая призма,
2 Дано:
которого
60°.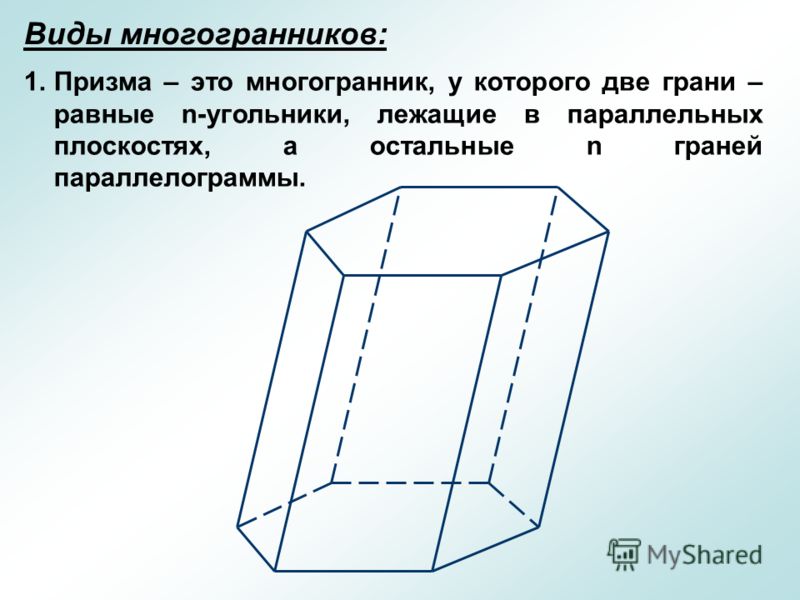
ABCD – ромб, ∠ВАD=60°, BB1=2,
Боковое ребро равно 2.
B
C ∠B1DВ= 45°.
45°
Найти: V диагональ призмы составляет
Меньшая
60°
с плоскостью основания угол 45°.
A
D
Найти объём призмы.
Решение.
V= Sосн ·h
S ABCD a b sin
∆ABD — равносторонний
AB=BD=2, т. к. ∆B1BD — равнобедренный
V 22 sin 60 2 4 3
Ответ:
4 3
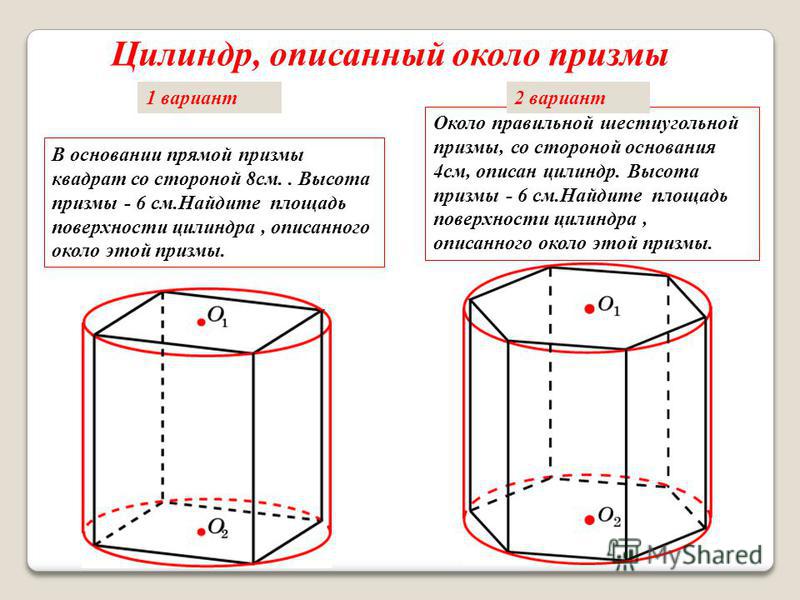
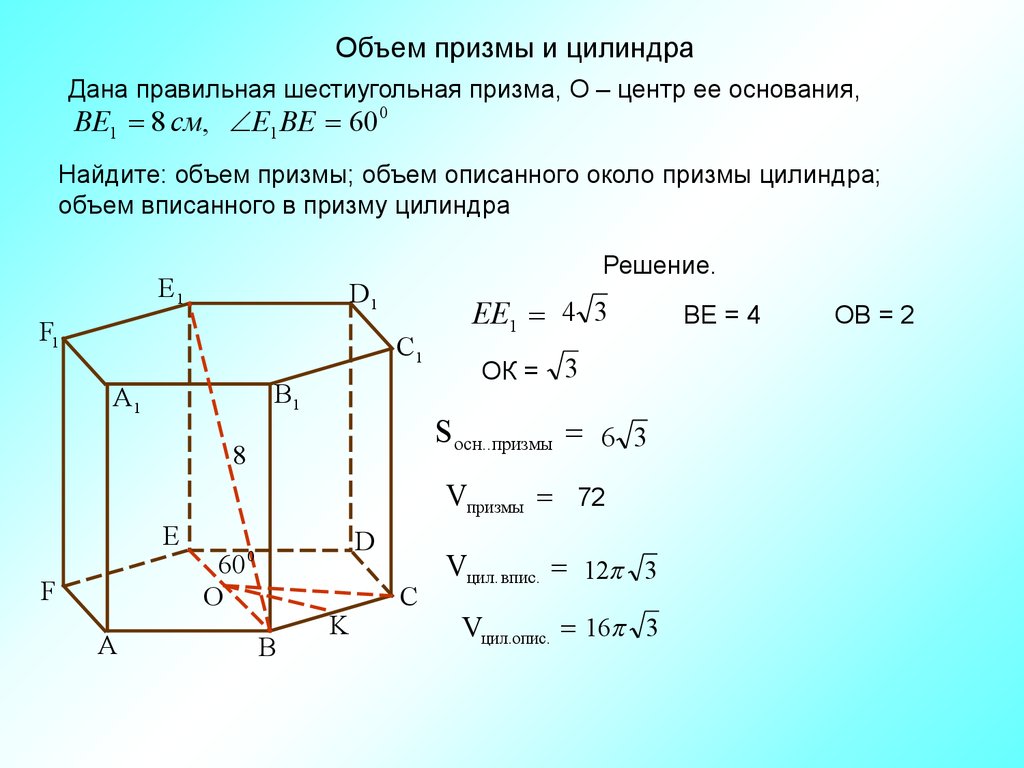
Что представляет собой
правильная шестиугольная
призма?
C1
B1
A1
F1
M1
B
C
D
A
M
F
Какая диагональ в этой призме
наибольшая?
C1
B1
A1
1
2
3
DM1
DB1
DA1
F1
ПОДУМАЙ
!
ПОДУМАЙ
!
ВЕРНО!
M1
B
C
D
A
M
F
№665
C1
B1
Наибольшая диагональ
D1 Дано:
правильной
шестиугольной
ABCDFM…M
1 — правильная
призмы равна 8призма.
см
шестиугольная
A1D = 8 см,
∠AА
C
1D = 30° с боковым
и составляет
Найти:V
ребром угол в 30°.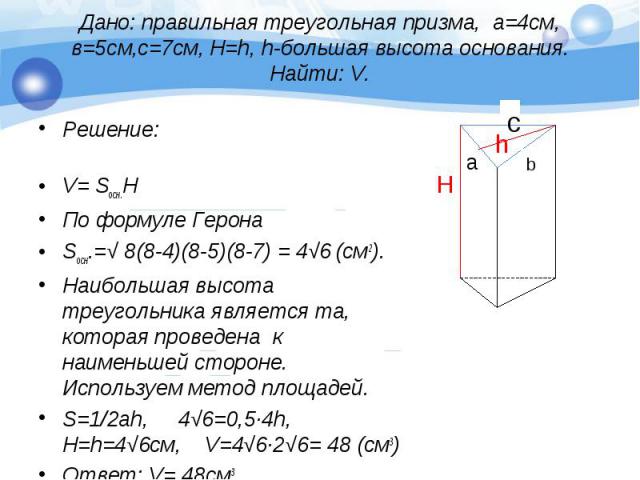
A1
F1
M1
B
D
A
О
Из ∆AА1D, где ∠А=90° находим AА1
F
M
Найти
объём призмы.
V= Sосн ·h
Решение.
3
АA1 DA1 cos 30 8
4 3см
2
2
OD=OA=R=2 см
S осн 6
а
4
AD=4 см
3
6 3см 2
V 6 3 4 3 72(см )
3
Ответ : 72см
3
Итог урока.
Ответить на вопросы:
а) Как вычисляется объем прямой призмы, основанием которой
является прямоугольный треугольник?
б) Как вычисляется объем правильной треугольной призмы?
в) Как вычисляется объем правильной четырехугольной призмы?
Рефлексия
Я конечно не Ай-да я,
ленился, но и
ай-да
очень не
молодец!
трудился
Скажу
опять,
что я не
понял
18. Домашнее задание.
№659(а), №663(а, б), п.65
Спасибо за
работу!
English
Русский
Правила
Введение в оптические призмы | Edmund Optics
Производство | Свет и преломление | Изображение Хиральность / Паритет | Типы | Руководство по выбору
Призмы представляют собой твердую стеклянную оптику, которая отшлифована и отполирована до геометрически и оптически значимых форм. Угол, положение и количество поверхностей помогают определить тип и функцию. Одно из самых узнаваемых применений призм, как продемонстрировал сэр Исаак Ньютон, состоит в том, чтобы разложить луч белого света на составляющие его цвета (рис. 1). Это приложение используется рефрактометром и спектрографическими компонентами. С момента этого первоначального открытия призмы использовались для «искривления» света внутри системы, «сворачивания» системы в меньшее пространство, изменения ориентации (также известной как хиральность или четность) изображения, а также для объединения или разделения оптических лучи с частично отражающими поверхностями. Эти виды использования распространены в приложениях с телескопами, биноклями, геодезическим оборудованием и множеством других.
Угол, положение и количество поверхностей помогают определить тип и функцию. Одно из самых узнаваемых применений призм, как продемонстрировал сэр Исаак Ньютон, состоит в том, чтобы разложить луч белого света на составляющие его цвета (рис. 1). Это приложение используется рефрактометром и спектрографическими компонентами. С момента этого первоначального открытия призмы использовались для «искривления» света внутри системы, «сворачивания» системы в меньшее пространство, изменения ориентации (также известной как хиральность или четность) изображения, а также для объединения или разделения оптических лучи с частично отражающими поверхностями. Эти виды использования распространены в приложениях с телескопами, биноклями, геодезическим оборудованием и множеством других.
Рис. 1: Рассеяние через призму
Примечательной характеристикой призм является их способность моделировать систему плоских зеркал для имитации отражения света внутри призмы. Замена зеркальных сборок, пожалуй, наиболее полезное применение призм, поскольку они и преломляют или преломляют свет, и изменяют четность изображения.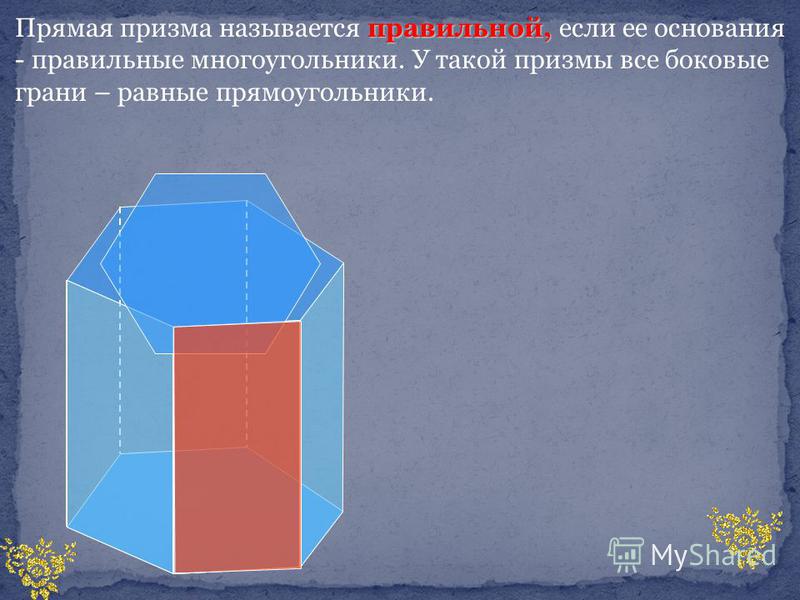 Часто требуется несколько зеркал для достижения результатов, аналогичных одной призме. Таким образом, замена одной призмы несколькими зеркалами снижает потенциальные ошибки юстировки, повышает точность и минимизирует размер и сложность системы.
Часто требуется несколько зеркал для достижения результатов, аналогичных одной призме. Таким образом, замена одной призмы несколькими зеркалами снижает потенциальные ошибки юстировки, повышает точность и минимизирует размер и сложность системы.
ПРОИЗВОДСТВО ПРИЗМ
Прежде чем углубляться в теорию призм, рассмотрим процесс их изготовления. Чтобы успешно использоваться в большинстве приложений, призмы должны быть изготовлены с очень строгими допусками и точностью. Из-за разнообразия форм, размеров и, самое главное, количества поверхностей крупномасштабный автоматизированный процесс изготовления призм практически невозможен. Кроме того, большинство высокоточных призм, как правило, изготавливаются в небольших количествах, а это означает, что автоматизированный процесс не нужен.
Сначала получается блок стекла (известный как «заготовка») определенного сорта и типа стекла. Этот блок затем шлифуется или генерируется металлическим кругом с алмазной связкой в почти готовый продукт. На этом этапе большая часть стекла удаляется быстро, в результате чего получаются плоские, но все еще шероховатые поверхности (рис. 2а). На данный момент размеры будущей призмы очень близки к желаемым характеристикам. Далее следует процесс тонкой шлифовки, при котором с поверхности удаляются подповерхностные разрывы; этот этап известен как сглаживание. Царапины, оставшиеся после первого этапа, удаляются на втором этапе (рис. 2б). После сглаживания стеклянные поверхности должны казаться мутными и непрозрачными. На обоих первых двух этапах поверхность призмы должна быть влажной, чтобы ускорить снятие стекла и предотвратить перегрев самого стекла.
На этом этапе большая часть стекла удаляется быстро, в результате чего получаются плоские, но все еще шероховатые поверхности (рис. 2а). На данный момент размеры будущей призмы очень близки к желаемым характеристикам. Далее следует процесс тонкой шлифовки, при котором с поверхности удаляются подповерхностные разрывы; этот этап известен как сглаживание. Царапины, оставшиеся после первого этапа, удаляются на втором этапе (рис. 2б). После сглаживания стеклянные поверхности должны казаться мутными и непрозрачными. На обоих первых двух этапах поверхность призмы должна быть влажной, чтобы ускорить снятие стекла и предотвратить перегрев самого стекла.
Третий этап включает полировку призмы до правильно заданной плоскостности поверхности. На этом этапе стекло натирают полиуретановым полировальным средством, смоченным «суспензией» — составом для оптической полировки, обычно состоящим из воды, смешанной с пемзой или оксидом церия (рис. 2с). Точная продолжительность этапа полировки сильно зависит от требуемых характеристик поверхности. После завершения полировки можно приступать к снятию фаски. На этом четвертом этапе края призмы подвергаются вращающейся алмазной пластине, чтобы слегка притупить острые края, полученные на вышеупомянутых этапах (рис. 2d). После снятия фаски готовая призма очищается, проверяется (как вручную, так и автоматически) и при необходимости покрывается антибликовым покрытием (AR) и/или металлическим зеркальным покрытием для дальнейшего улучшения общего пропускания и/или отражения. Хотя процесс намного сложнее и может потребовать больше итераций или операций из-за количества поверхностей на призме, этапы создания, сглаживания, полировки и снятия фаски примерно показаны на рисунках 2a-2d.
После завершения полировки можно приступать к снятию фаски. На этом четвертом этапе края призмы подвергаются вращающейся алмазной пластине, чтобы слегка притупить острые края, полученные на вышеупомянутых этапах (рис. 2d). После снятия фаски готовая призма очищается, проверяется (как вручную, так и автоматически) и при необходимости покрывается антибликовым покрытием (AR) и/или металлическим зеркальным покрытием для дальнейшего улучшения общего пропускания и/или отражения. Хотя процесс намного сложнее и может потребовать больше итераций или операций из-за количества поверхностей на призме, этапы создания, сглаживания, полировки и снятия фаски примерно показаны на рисунках 2a-2d.
Рисунок 2A: Процесс производства PRISM: генерирование стадии
Рисунок 2B: ПРОЦЕСС ПРИМА Процесс: Стадия сглаживания
Рисунок 2C: PRISM Процесс производства: Полировальная стадия
Рис. Стадия снятия фаски В процессе изготовления призмы необходимо постоянно регулировать и закреплять каждую обрабатываемую поверхность. На каждом этапе процесса изготовления призмы, от создания до блокировки и контакта, требуется, чтобы опытный оптик вручную осматривал и регулировал обрабатываемые поверхности призмы. В результате это чрезвычайно трудоемко и требует опыта и навыков для завершения. Весь процесс часто требует значительного количества времени, работы и концентрации. Понимание того, как работает призма, является ключом к решению, какой тип призмы лучше всего подходит для конкретного применения. (1) $$ n_1 \sin\! \left(\theta_1\right)=n_2 \sin \! \left(\theta_2\right) $$ Где $ \small{n_1} $ – индекс падающей среды, $ \small{\theta_1} $ – угол падающего луча, $ \small{n_2} $ — индекс преломленной/отраженной среды, а $ \small{\theta_2} $ — угол преломленного/отраженного луча. Закон Снеллиуса описывает взаимосвязь между углами падения и прохождения, когда луч проходит между несколькими средами (рис. 3). Рис. 3: Закон Снеллиуса и полное внутреннее отражение Призма отличается своей способностью отражать путь луча без необходимости специального покрытия, такого как при использовании зеркала. Это достигается за счет явления, известного как полное внутреннее отражение (ПВО). ПВО возникает, когда угол падения (угол падающего луча, измеренный от нормали) больше критического угла $ \small{\theta_c} $: (2) $$ \sin\!\left(\theta_c\ справа)=\frac{n_2}{n_1} $$ Где $ \small{n_1} $ – показатель преломления среды, из которой исходит луч, а $ \small{n_2} $ – показатель преломления среды, из которой выходит луч. При критическом угле угол преломления равен 90°. Обращаясь к рисунку 3, обратите внимание, что TIR происходит только в том случае, если $ \small{\theta} $ превышает критический угол. Если угол ниже критического угла, то передача будет происходить вместе с отражением, как указано в законе Снеллиуса. Если поверхность призмы не соответствует требованиям TIR для требуемого угла (углов), необходимо использовать отражающее покрытие. Вот почему в некоторых приложениях требуются версии призмы с покрытием, которые в противном случае хорошо работали бы без покрытия в другом приложении. Важным аспектом визуализации через призму является ориентация изображения (четность), иначе называемая ориентацией изображения. Это вводится каждый раз, когда траектория луча попадает на плоское зеркало, любую плоскую отражающую поверхность или поверхность призмы под углом, создающим ПВО. Рис. 4: Праворукость или четность Рис. 5: Леворукость или нечетность В дополнение к четности существует три типа изменения изображения (рис. 6). Инверсия — это переворот изображения по горизонтальной оси, тогда как реверсия — это переворот изображения по вертикальной оси. Когда оба выполняются одновременно, происходит поворот изображения на 180°, и четность не меняется. Другой способ думать о четности — определить ее как определение, если смотреть назад против направления распространения либо на объект, либо на изображение в его оптическом пространстве (рис. Рис. 6: Инверсия (сверху), реверсия (посередине) и вращение (снизу) Рис. 7: Как определяется четность При использовании призмы учитывайте следующие четыре момента: Некоторые отражатели, такие как прямоугольные и крышные, часто имеют заданный допуск пирамиды или допустимую ошибку пирамиды. Это не один из физических углов призмы, а скорее способ описать точность параллельных поверхностей призмы по отношению друг к другу. Если все поверхности вытянуты в идеальную призму, одна и та же форма сохранится навсегда. Типичные допуски пирамиды для призм прецизионного качества составляют от 1 до 3 угловых минут. Призмы коммерческого качества часто имеют допуски в диапазоне 5-10 угловых минут. Допуск пирамиды — это, по существу, допуск наклона на поверхностях, перпендикулярных треугольникам треугольной призмы. Обычно то, как призмы преломляют свет, рассматривается в двухмерной плоскости (X-Z). Наклон от допуска пирамиды будет перпендикулярен этому в плоскости Y. Для многих систем ошибка пирамиды практически не влияет на производительность и может быть скорректирована с помощью наклона призмы. Существует четыре основных типа призм: рассеивающие призмы, отклоняющие или отражающие призмы, призмы вращения и призмы смещения. Отклоняющие, смещающие и вращающиеся призмы широко используются в приложениях для обработки изображений; дисперсионные призмы предназначены исключительно для рассеивания света, поэтому они не подходят для приложений, требующих качественного изображения. Дисперсия призмы зависит от геометрии призмы и ее кривой дисперсии показателя, основанной на длине волны и показателе преломления подложки призмы. Угол минимального отклонения определяет наименьший угол между падающим и прошедшим лучами (рис. 8). Длина волны зеленого света отклоняется больше, чем красного, а синего больше, чем красного и зеленого; красный обычно определяется как 656,3 нм, зеленый как 587,6 нм и синий как 486,1 нм. Рис. 8: Дисперсия через призму Призмы, которые отклоняют траекторию луча, поворачивают изображение или просто смещают изображение от его исходной оси, полезны во многих системах визуализации. Отклонения лучей обычно делают под углами 45°, 60°, 90° и 180°. Это помогает уменьшить размер системы или отрегулировать путь лучей, не влияя на остальные настройки системы. Призмы вращения, такие как призмы голубя, используются для поворота изображения после его инвертирования. Призмы смещения сохраняют направление пути луча, но корректируют его отношение к нормали. Чтобы помочь в выборе лучших призм для конкретных приложений, рассмотрите следующее руководство по выбору призм, наиболее часто используемых в оптике, обработке изображений и фотонике. Чтобы начать, нажмите синюю кнопку «Моделирование» в верхнем левом углу. Далее: Нажмите на любой детектор, чтобы увидеть поперечное сечение света в этой позиции В некоторых симуляциях можно изменить положение или материал призм, нажав на призму. внутри призмы. Эта кнопка вторая слева Вращение и увеличение экрана с помощью мыши и/или коврика для мыши После внесения изменений повторно запустите симуляцию, снова нажав кнопку симуляции, чтобы увидеть обновленный детектор показания Руководство по выбору призмы Равносторонние призмы — дисперсия Применение Узнать больше Призмы Литтроу — Дисперсия, отклонение Применение Узнать больше Прямоугольные призмы – отклонение, смещение Применение Узнать больше Пентапризмы — Отклонение Применение Узнать больше Полупента призмы — отклонение Применение Узнать больше Крышная призма Amici — отклонение Применение Узнать больше Призмы Шмидта — Отклонение Применение Узнать больше Ретрорефлекторы (трехгранные призмы) — отклонение, смещение Применение Узнать больше Клиновые призмы — отклонение, вращение Применение Узнать больше Ромбовидные призмы — перемещение Применение Узнать больше Призмы Dove — вращение Применение Узнать больше Пара анаморфотных призм — расширение Приложение Узнать больше Гомогенизирующие стержни световода – гомогенизация Применение Узнать больше Гомогенизирующие стержни с конической тонкой трубкой – гомогенизация Применение Узнать больше В этом введении дается обзор производственного процесса и теории, связанной с призмами, а также выбор, который поможет вам найти лучшую призму для вашего приложения. Анимация от 3DOptix. Был ли этот контент полезен для вас? Спасибо за оценку этого контента! Ссылки на каждую отдельную главу Цветного атласа гониоскопии доступны по ссылке «Главы» ниже. Закрепление призмы на месте включает один из двух методов: блокировку и контакт. Блокировка предполагает размещение призмы в металлическом инструменте с горячим воском. Контактирование, с другой стороны, представляет собой процесс оптического соединения, осуществляемый при комнатной температуре, когда две чистые стеклянные поверхности скрепляются друг с другом просто за счет взаимодействия Ван-дер-Ваальса. Контакт используется, если требуются допуски высокой точности, поскольку он не требует дополнительных настроек на этапах создания, сглаживания или полировки для учета толщины воска между поверхностью призмы и контактным блоком.
Закрепление призмы на месте включает один из двух методов: блокировку и контакт. Блокировка предполагает размещение призмы в металлическом инструменте с горячим воском. Контактирование, с другой стороны, представляет собой процесс оптического соединения, осуществляемый при комнатной температуре, когда две чистые стеклянные поверхности скрепляются друг с другом просто за счет взаимодействия Ван-дер-Ваальса. Контакт используется, если требуются допуски высокой точности, поскольку он не требует дополнительных настроек на этапах создания, сглаживания или полировки для учета толщины воска между поверхностью призмы и контактным блоком. ТЕОРИЯ: СВЕТА И ПРЕЛОМЛЕНИЯ
 Для этого важно сначала понять, как свет взаимодействует с оптической поверхностью. Это взаимодействие описывается законом преломления Снелла:
Для этого важно сначала понять, как свет взаимодействует с оптической поверхностью. Это взаимодействие описывается законом преломления Снелла: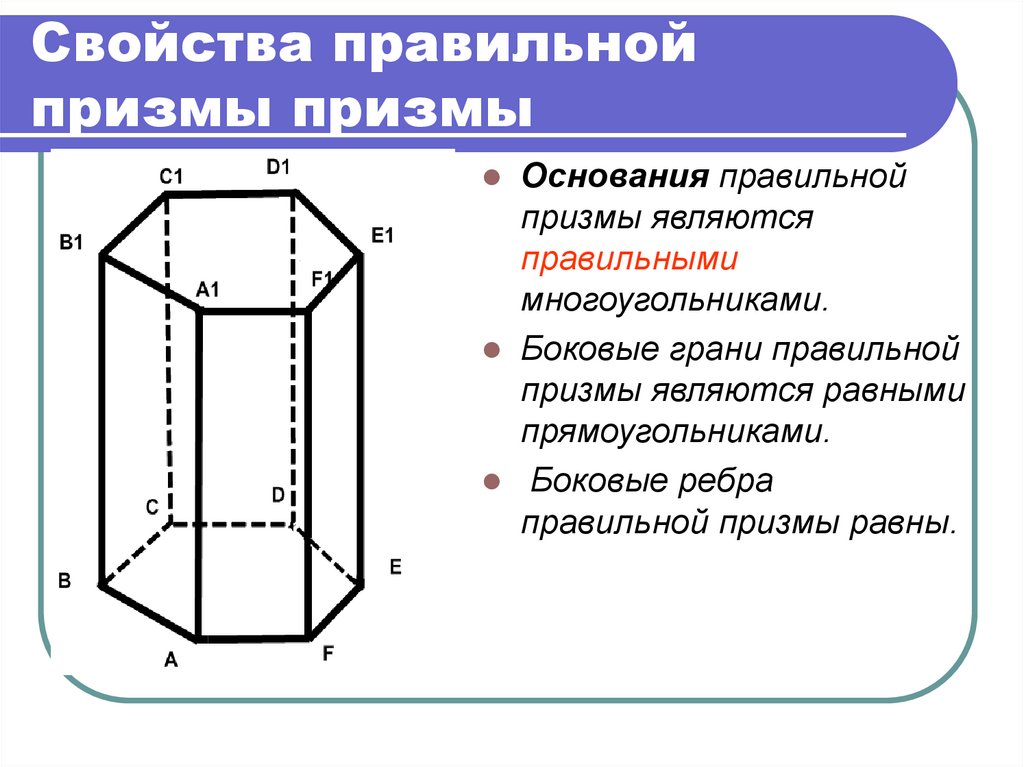 Важно отметить, что TIR происходит только тогда, когда свет проходит от среды с высоким показателем преломления к среде с низким показателем преломления.
Важно отметить, что TIR происходит только тогда, когда свет проходит от среды с высоким показателем преломления к среде с низким показателем преломления. ТЕОРИЯ: ПРАВИЛЬНОСТЬ ИЗОБРАЖЕНИЯ/ЧЕТНОСТЬ
 Различают два типа рук: правую и левую. Праворукость (рисунок 4) описывает случай, когда изображение претерпевает четное число отражений, что приводит к способности четко читать его (при условии, что изображение является текстом) по крайней мере в одной позиции. Леворукость (рис. 5) описывает случай, когда изображение претерпевает нечетное число отражений, что приводит к неравномерности положения изображения, сравнимой с тем, что можно увидеть в зеркале.
Различают два типа рук: правую и левую. Праворукость (рисунок 4) описывает случай, когда изображение претерпевает четное число отражений, что приводит к способности четко читать его (при условии, что изображение является текстом) по крайней мере в одной позиции. Леворукость (рис. 5) описывает случай, когда изображение претерпевает нечетное число отражений, что приводит к неравномерности положения изображения, сравнимой с тем, что можно увидеть в зеркале. 7).
7). ЧТО ТАКОЕ ДОПУСТИМОСТЬ ПИРАМИДЫ?
 Это будет ошибкой пирамиды, равной нулю. На самом деле, параллельные поверхности призмы будут иметь небольшой уровень несоосности, что при расширении поверхностей призмы в конечном итоге приведет к образованию пирамиды. Угол при вершине этой теоретической пирамиды является ошибкой пирамиды. Это вычисляется из проекции одного ребра призмы на линию, которая находится между ребрами на противоположной грани призмы.
Это будет ошибкой пирамиды, равной нулю. На самом деле, параллельные поверхности призмы будут иметь небольшой уровень несоосности, что при расширении поверхностей призмы в конечном итоге приведет к образованию пирамиды. Угол при вершине этой теоретической пирамиды является ошибкой пирамиды. Это вычисляется из проекции одного ребра призмы на линию, которая находится между ребрами на противоположной грани призмы.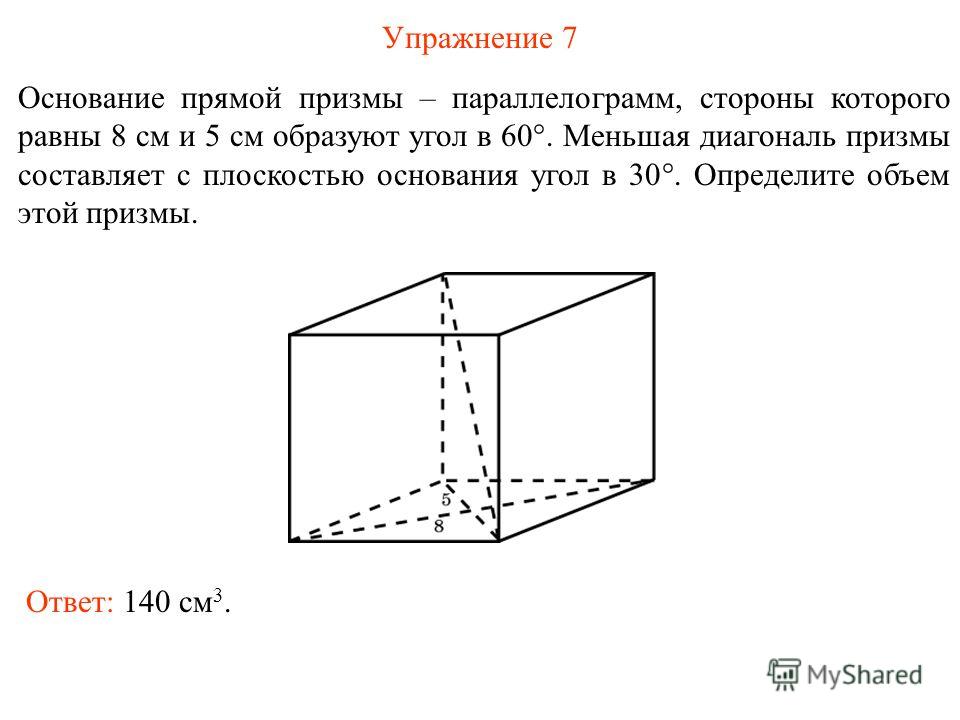 Но эта спецификация может быть важна в некоторых приложениях, где наклон по Y нельзя изменить механически, чтобы компенсировать эту ошибку. Для этих приложений допуски пирамид должны строго контролироваться. Это может быть особенно проблематично для крышных призм.
Но эта спецификация может быть важна в некоторых приложениях, где наклон по Y нельзя изменить механически, чтобы компенсировать эту ошибку. Для этих приложений допуски пирамид должны строго контролироваться. Это может быть особенно проблематично для крышных призм. ТИПЫ ПРИЗМ
Дисперсионные призмы
Отклонение, вращение и смещение призмы
Руководство по выбору призм
Несколько частей приведенного ниже руководства по выбору включают интерактивные симуляции, позволяющие увидеть, как эти призмы влияют на падающий свет.

Функция Функция Функция Функция Функция Функция Функция Функция Функция Функция Функция Функция Функция Функция  Чтобы узнать о некоторых примерах применения призмы, см. раздел Примеры применения оптической призмы.
Чтобы узнать о некоторых примерах применения призмы, см. раздел Примеры применения оптической призмы. Принципы гониоскопии — Американская академия офтальмологии
Главы
Непосредственный осмотр передней камеры нормального глаза ( 3-1 ) невозможен. Свет от стыка радужной оболочки и роговицы падает на границу раздела слеза-воздух под небольшим углом и полностью отражается обратно в глаз (9).0007 3-2 ). Это принцип полного внутреннего отражения. Если свет из внутренней части глаза падает на роговицу под углом более 46° (критический угол), свет выходит из глаза и становится видна трабекулярная сеть (Shields, 1992). В редких случаях это может произойти в глазах с кератоконусом, кератоглобусом или тяжелой близорукостью ( 3‑3 ).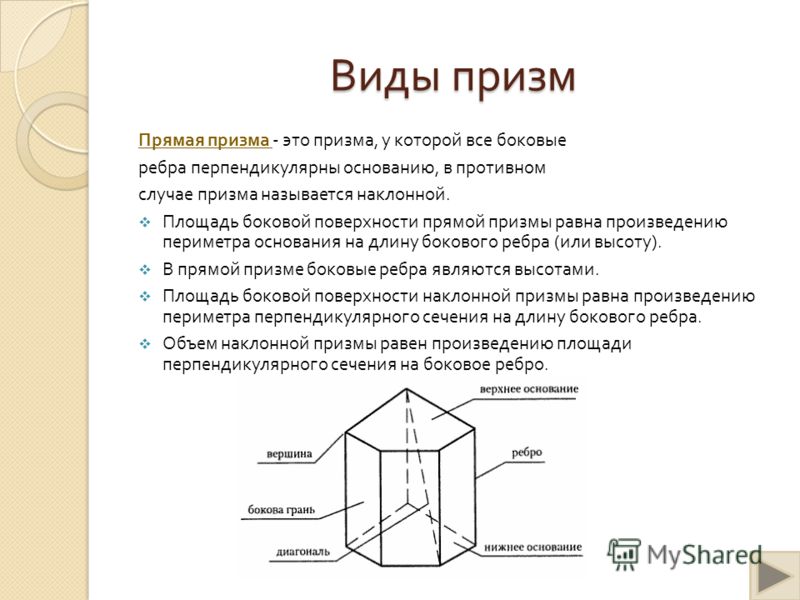 Угол доступа к трабекулярной сети может быть изменен, если лимб вдавлен, как показано Трантасом в его первоначальном описании гониоскопии (9).0007 3‑4 ) (Трантас, 1907).
Угол доступа к трабекулярной сети может быть изменен, если лимб вдавлен, как показано Трантасом в его первоначальном описании гониоскопии (9).0007 3‑4 ) (Трантас, 1907).
В современной гониоскопии контактные линзы используются для преодоления проблемы полного внутреннего отражения. Используются два основных типа линз: прямая линза и непрямая линза.
3-1 Вид с помощью щелевой лампы, попытка визуализировать угол нормальным глазом. Угловые структуры не видны из-за полного внутреннего отражения
3-2 Свет от угла передней камеры (а) подвергается полному внутреннему отражению на границе слеза-воздух и не виден исследователю.
3-3 В глазу с кератоконусом свет от трабекулярной сети ( a ) падает на роговицу под достаточно крутым углом, чтобы наблюдатель мог непосредственно визуализировать трабекулярную сеть ( Obs .). Это необычная ситуация.
3-4 Вдавление лимба позволяет видеть угловые структуры (а) без линзы. Таким способом очень трудно получить неискаженное изображение.
Прямая гониоскопия
Прямая гониоскопия выполняется с крутовыпуклой линзой, которая позволяет свету под углом выходить из глаза ближе к перпендикуляру на границе между линзой и воздухом ( 3‑5 ). Линза Кеппе ( 3‑6 ), представляющая собой линзу с оптической силой 50 диоптрий, надевается на глаз лежачего пациента с использованием физиологического раствора для перекрытия зазора между линзой и роговицей ( 3‑7 ). Исследователь наблюдает за углом через ручной бинокулярный микроскоп, который уравновешен для удобства обращения. Освещение обеспечивается источником света, который держат в другой руке ( 3-8 ). Линза Кеппе увеличивает в 1,5 раза. Это, в сочетании с увеличением окуляров в 16 раз, дает общее увеличение в 24 раза. Существуют линзы Koeppe нескольких размеров, от младенцев до взрослых.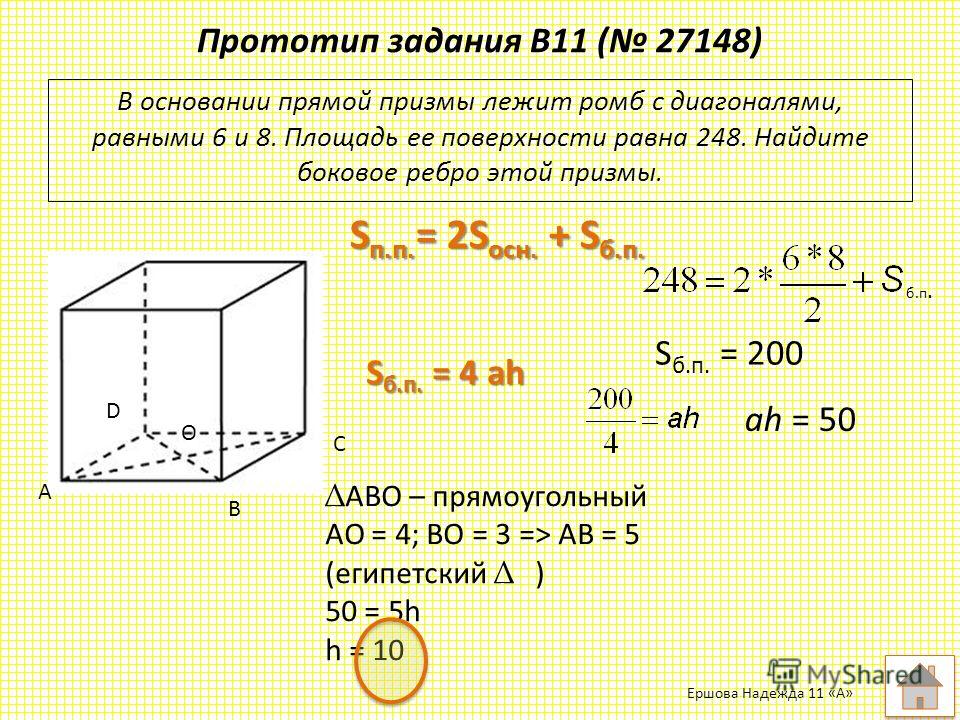
Прямые линзы используются для хирургических процедур, таких как гониотомия и гониосинехиализ. Чаще всего используются линзы Хоскинса-Баркана (с 3‑9 по 3‑11 ) и Свон-Джейкобса ( 3‑12 ). Эти линзы также можно использовать для осмотра младенцев, находящихся под седацией, с помощью операционного микроскопа или портативной щелевой лампы (9).0007 3-13 и 3-14 ).
3-5 Прямые гониоскопические линзы изменяют угол поверхности раздела с воздухом, так что свет от трабекулярной сети (а) выходит более перпендикулярно.
3-6 Линза Кеппе для прямой гониоскопии доступна в нескольких размерах. (С любезного разрешения Ocular Instruments.)
3-7 Солевой раствор используется для перекрытия зазора между линзой Кеппе и роговицей у пациента, лежащего на спине. (Любезно предоставлено Полом Р. Лихтером, доктором медицинских наук, Мичиганский университет, и А. Тимом Джонсоном, доктором медицинских наук, отделение офтальмологии и визуальных наук, Университет Айовы.)
Тимом Джонсоном, доктором медицинских наук, отделение офтальмологии и визуальных наук, Университет Айовы.)
3-8 Обследование лежащего на спине пациента с линзой Кеппе с использованием уравновешенного биомикроскопа и осветителя Баркана. (С любезного разрешения Пола Р. Лихтера, доктора медицинских наук, Мичиганский университет, и А. Тима Джонсона, доктора медицинских наук, отделение офтальмологии и визуальных наук Университета Айовы.) 3-10 , 3-11 Хирургические контактные линзы Хоскинса-Баркана трех размеров (для младенцев, недоношенных младенцев или взрослых). Эта прямая линза используется с лупами или операционным микроскопом для гониотомии и других угловых операций. (Любезно предоставлено Ocular Instruments.)
3-12 Хирургические контактные линзы Swan-Jacobs. Эта прямая линза используется с лупами или операционным микроскопом для гониотомии и других угловых операций. (С любезного разрешения Ocular Instruments. )
)
3-13 Гониоскопия может быть выполнена младенцам, находящимся под седацией, с прямой контактной линзой и операционным микроскопом или портативной щелевой лампой. Здесь линза Свана-Джейкобса используется с портативной щелевой лампой для исследования глаза ребенка с первичной инфантильной глаукомой, находящегося под седацией.
3-14 Вид через линзу Свана-Джейкобса на угол ребенка с первичной детской глаукомой.
Непрямая гониоскопия
Линзы, используемые в непрямой гониоскопии, используют зеркала для преодоления полного внутреннего отражения. Зеркало перенаправляет свет под углом таким образом, чтобы он выходил из глаза перпендикулярно границе линза-воздух ( 3‑15 ). Обследование проводится на щелевой лампе с использованием гибкой системы освещения и увеличения последней.
Трехзеркальная линза Гольдмана ( 3‑16 и 3‑17 ) имеет одно зеркало, предназначенное для наблюдения за углом. Есть два дополнительных зеркала для осмотра периферии сетчатки. Линза Гольдмана соединена с роговицей с помощью вязкой метилцеллюлозной жидкости. Линза имеет широкую (12 мм) площадь контакта с глазным яблоком и при приложении давления может искусственно закрыть угол или рефлюкс крови в шлеммов канал. Однозеркальная линза Гольдмана имеет только гониоскопическое зеркало ( 3-18 ). Лазерная линза Ritch для трабекулопластики ( 3-19 ) аналогична линзе Гольдмана, за исключением того, что все четыре ее зеркала направлены под углом; два зеркала обращены к углу 59°, а другая пара приближается к нему под углом 64°. Перед одним из зеркал 59° и одним из зеркал 64° находятся выпуклые кнопки, увеличивающие увеличение в 1,4 раза и концентрирующие лазерную энергию (Ritch, 1985). Объектив Magna View ( 3‑20 и 3‑21 ) — это однозеркальный объектив, аналогичный однозеркальному объективу Гольдмана, за исключением того, что он имеет более широкое поле зрения и обеспечивает увеличение ×1,3.
Есть два дополнительных зеркала для осмотра периферии сетчатки. Линза Гольдмана соединена с роговицей с помощью вязкой метилцеллюлозной жидкости. Линза имеет широкую (12 мм) площадь контакта с глазным яблоком и при приложении давления может искусственно закрыть угол или рефлюкс крови в шлеммов канал. Однозеркальная линза Гольдмана имеет только гониоскопическое зеркало ( 3-18 ). Лазерная линза Ritch для трабекулопластики ( 3-19 ) аналогична линзе Гольдмана, за исключением того, что все четыре ее зеркала направлены под углом; два зеркала обращены к углу 59°, а другая пара приближается к нему под углом 64°. Перед одним из зеркал 59° и одним из зеркал 64° находятся выпуклые кнопки, увеличивающие увеличение в 1,4 раза и концентрирующие лазерную энергию (Ritch, 1985). Объектив Magna View ( 3‑20 и 3‑21 ) — это однозеркальный объектив, аналогичный однозеркальному объективу Гольдмана, за исключением того, что он имеет более широкое поле зрения и обеспечивает увеличение ×1,3.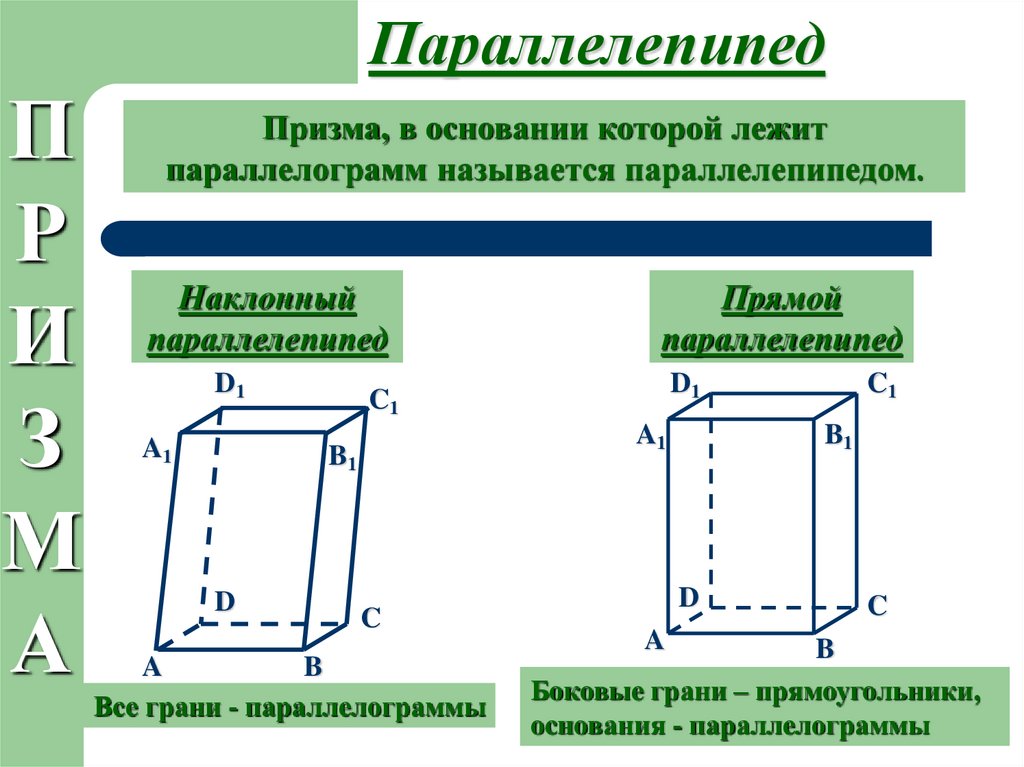 Он был разработан для подачи лазерной энергии в угол и фотосъемки.
Он был разработан для подачи лазерной энергии в угол и фотосъемки.
3-15 Непрямые гониоскопические линзы используют зеркала или призмы, не имеют ручки для отражения света от радужно-роговичного угла ( a ), так что он выходит из глаза перпендикулярно лицу контактные линзы.
3‑16 , 3‑17 Трехзеркальная линза Гольдмана. Самое короткое зеркало предназначено для изучения угла. Два других зеркала предназначены для осмотра периферии сетчатки. Как и все непрямые линзы, центральную область можно использовать для осмотра глазного дна. (С любезного разрешения Haag-Streit.)
3-18 Однозеркальная линза типа Гольдмана. (С разрешения компании Ocular Instruments.)
3-19 Линзы для лазерной трабекулопластики Ritch. Два зеркала с углом наклона 59° предназначены для обзора под нижним углом, а два зеркала с углом обзора 64° предназначены для обзора под углом выше. Выпуклая кнопка перед одним зеркалом 59° и одним зеркалом 64° обеспечивает дополнительное увеличение для осмотра и лазерного лечения. (Предоставлено Ocular Instruments.)
Выпуклая кнопка перед одним зеркалом 59° и одним зеркалом 64° обеспечивает дополнительное увеличение для осмотра и лазерного лечения. (Предоставлено Ocular Instruments.)
3‑20, 3‑21 Объектив Magna View представляет собой однозеркальный объектив типа Гольдмана. У него более широкая область обзора, чем у однозеркальной линзы Гольдмана, и выпуклая передняя поверхность, обеспечивающая небольшое увеличение. Эта линза была разработана для подачи лазерной энергии под углом. (Предоставлено Ocular Instruments.)
Линза Познера ( 3-22 ) имеет четыре идентичных зеркала, которые позволяют исследовать четыре квадранта без вращения линзы ( 3-23 ). Повернув объектив всего на 11°, можно увидеть небольшие участки между зеркалами. Потому что объектив имеет небольшой (9мм) площадь соприкосновения с роговицей, угол можно углубить, надавив на линзу (вдавливающая гониоскопия). Небольшой зазор между хрусталиком и роговицей заполняется слезами или местным анестетиком. Это предохраняет роговицу от вязких жидкостей и позволяет четко осмотреть и сфотографировать диск зрительного нерва после гониоскопии. Линза Zeiss ( 3‑24 и 3‑25 ) аналогична линзе Posner, но сделана из стекла, а не из пластика. Его больше нет в продаже. Линза Суссмана ( 3‑26 и 3‑27 ) также похожа на линзу Познера, за исключением того, что у нее нет ручки.
Это предохраняет роговицу от вязких жидкостей и позволяет четко осмотреть и сфотографировать диск зрительного нерва после гониоскопии. Линза Zeiss ( 3‑24 и 3‑25 ) аналогична линзе Posner, но сделана из стекла, а не из пластика. Его больше нет в продаже. Линза Суссмана ( 3‑26 и 3‑27 ) также похожа на линзу Познера, за исключением того, что у нее нет ручки.
Особо следует упомянуть гониопризму Аллена-Торпа ( 3-28 и 3-29 ), которая использовалась при подготовке всех картин, воспроизведенных в этом Атласе (Allen et al, 1954). Вместо зеркал этот объектив имеет четыре призмы. У него есть фланец, который удерживает его на месте ( 3‑30 ), и для его соединения с роговицей требуется метилцеллюлоза. Объектив больше не продается.
3-22 Набор четырехзеркальных линз Познера с фиксированной ручкой и пластиковой линзой.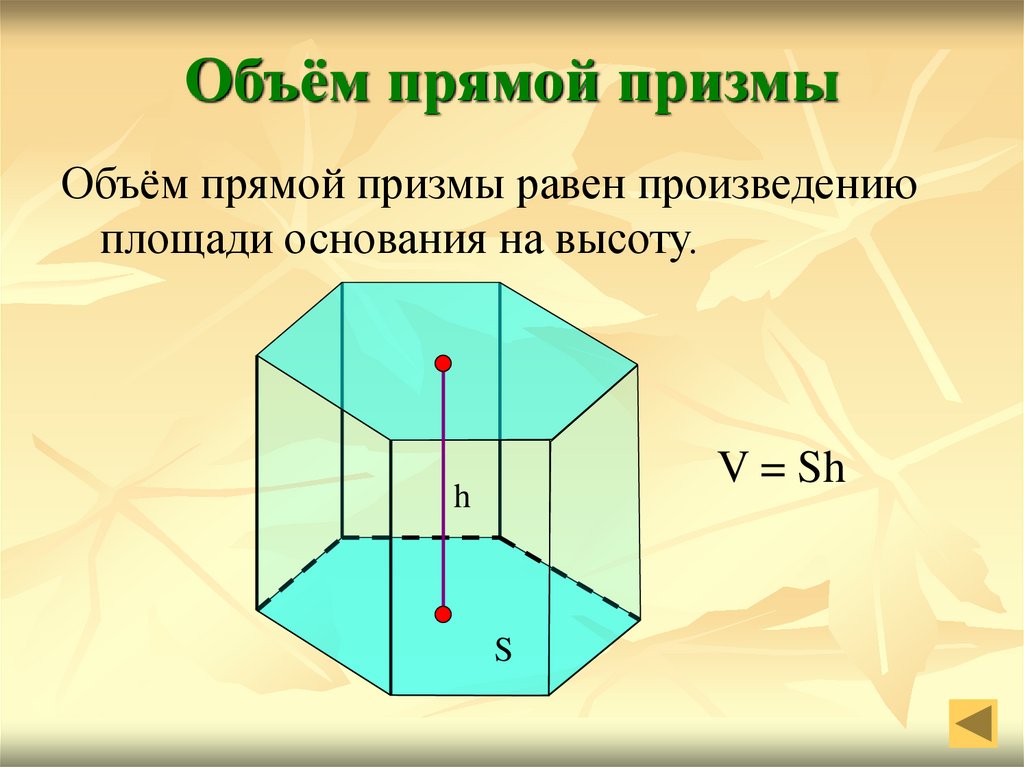 Этот объектив имеет четыре одинаковых зеркала для быстрой гониоскопии. Соединительный раствор метилцеллюлозы не требуется. Небольшая площадь контакта позволяет проводить индентальную гониоскопию. Этот объектив очень похож на четырехзеркальный объектив Zeiss, который больше не продается. (Предоставлено Ocular Instruments.)
Этот объектив имеет четыре одинаковых зеркала для быстрой гониоскопии. Соединительный раствор метилцеллюлозы не требуется. Небольшая площадь контакта позволяет проводить индентальную гониоскопию. Этот объектив очень похож на четырехзеркальный объектив Zeiss, который больше не продается. (Предоставлено Ocular Instruments.)
3-23 Четыре квадранта, видимые через четырехзеркальный объектив Zeiss.
3‑24, 3‑25 Четырёхзеркальная линза Zeiss на вилке Unger (Carl Zeiss).
3‑26, 3‑27 Четырехзеркальный объектив Sussman похож на объектив Zeiss или Posner, но без ручки. Некоторые исследователи предпочитают держать линзу прямо. (С разрешения Ocular Instruments.)
3-28 , 3-29 Гониопризма Аллена-Торпа. Четыре призмы позволяют исследовать все четыре квадранта. Линза подвешена в оправе с помощью тонкой пружины, которая прижимает призму к роговице. Оправа удерживает объектив между веками. (Предоставлено Bausch & Lomb.)
Оправа удерживает объектив между веками. (Предоставлено Bausch & Lomb.)
3-30 Гониопризма Аллена-Торпа удерживается на месте своей рамой. Обе руки свободны для управления щелевой лампой.
Сравнение прямой и непрямой гониоскопии
Как прямая, так и непрямая гониоскопия имеют свои преимущества и недостатки.
Хотя прямая гониоскопия больше не применяется за пределами операционной, она имеет определенные преимущества перед непрямой гониоскопией. Прямая гониоскопия, как следует из этого термина, обеспечивает прямой обзор угла, а не зеркальное изображение, даваемое непрямыми линзами. Прямая гониоскопия позволяет исследователю легче изменять угол обзора, например, чтобы можно было рассмотреть кривизну радужной оболочки. Вид при прямой гониоскопии более панорамный, чем при непрямой гониоскопии. Две линзы Кеппе можно использовать для сравнения углов двух глаз, чтобы определить, не пострадал ли один глаз от травматической рецессии.
Основным недостатком прямой гониоскопии является ее неудобство.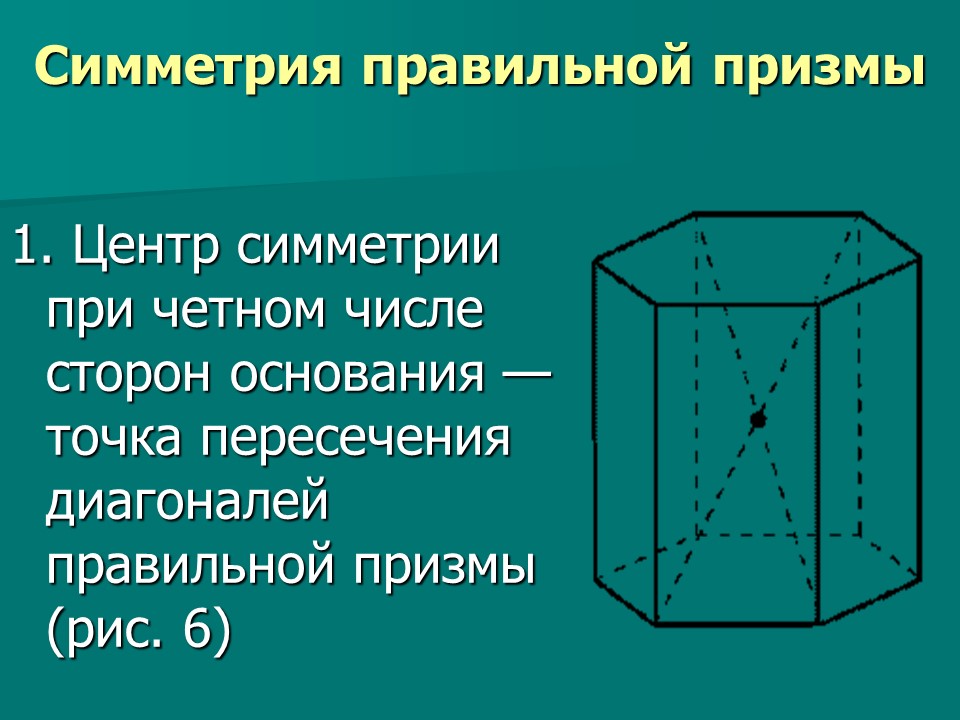 Больному приходится лежать, как правило, в специальной комнате со специальным оборудованием. Неудобство прямой гониоскопии привело к разработке системы van Herick для оценки глубины передней камеры на основе осмотра с помощью щелевой лампы. Van Herick заявил, что «при рутинном обследовании пациентов без глаукомы нецелесообразно проводить гониоскопию» (van Herick et al, 1969). К счастью, удобство непрямой гониоскопии позволяет быстро выполнить ее в рамках рутинного обследования пациентов с глаукомой.
Больному приходится лежать, как правило, в специальной комнате со специальным оборудованием. Неудобство прямой гониоскопии привело к разработке системы van Herick для оценки глубины передней камеры на основе осмотра с помощью щелевой лампы. Van Herick заявил, что «при рутинном обследовании пациентов без глаукомы нецелесообразно проводить гониоскопию» (van Herick et al, 1969). К счастью, удобство непрямой гониоскопии позволяет быстро выполнить ее в рамках рутинного обследования пациентов с глаукомой.
Непрямые линзы имеют ряд преимуществ, которые сделали их предпочтительными для большинства офтальмологов. Первое преимущество, характерное для четырехзеркальных линз, заключается в том, что они не требуют вязких связующих агентов. Это особенно важно, если пациенту необходимо сделать фотографию глазного дна во время одного визита. Гониоскопию можно быстро выполнить под тем же анестетиком, что и при тонометрии. Кроме того, при выполнении непрямой гониоскопии с любым объективом не требуется специального оборудования.