Плоскость это 5 класс: Плоскость — что это такое? Как обозначается?

Плоскость, прямая, луч | Школьная математика. Математика 5 класс

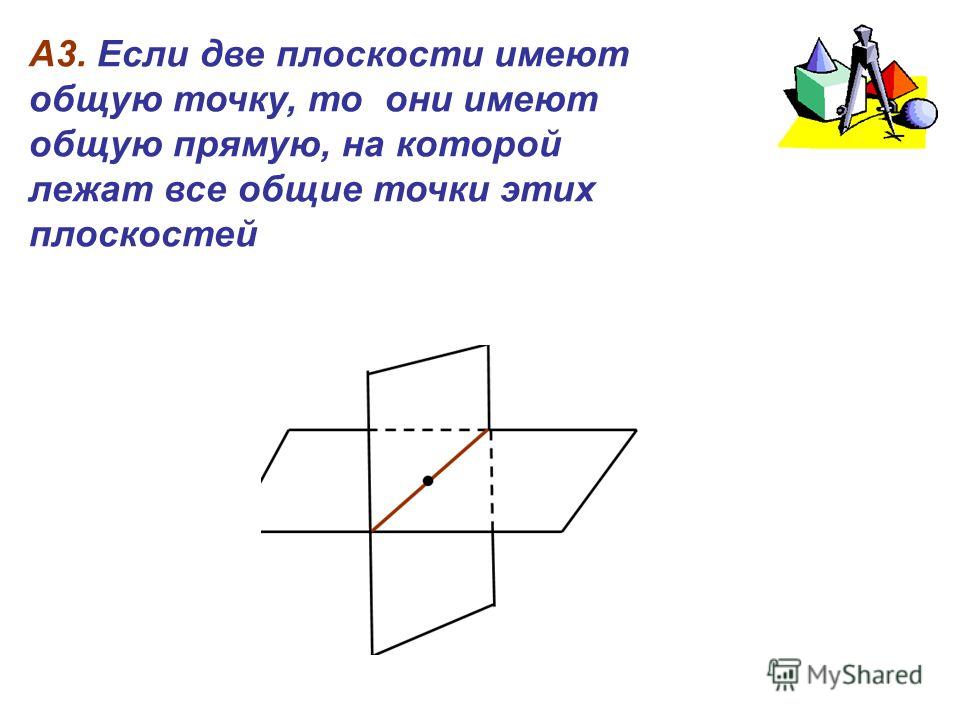
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Запомните

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Запомните

Каждой ваше пожертвование увеличивает количество полезной и интересной информации на сайте Easy-Math.ru!

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем, что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.

Обозначение прямой

В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита.

Иногда обозначение прямой линии происходит при помощи двух точек, которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.

Например, на рисунке 1 обозначены такие прямые:

• c
• KL

Рис. 1 Обозначение прямой линии

Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек.

Рис. 2 Обозначение прямой с несколькими точками

На рисунке 2 видно, что на одной прямой b лежат четыре точки: D, G, H, O. Поэтому данную прямую мы можем назвать любым из этих семи имен: b, DG, DH, DO, GH, GO или HO.

Некоторые свойства прямой

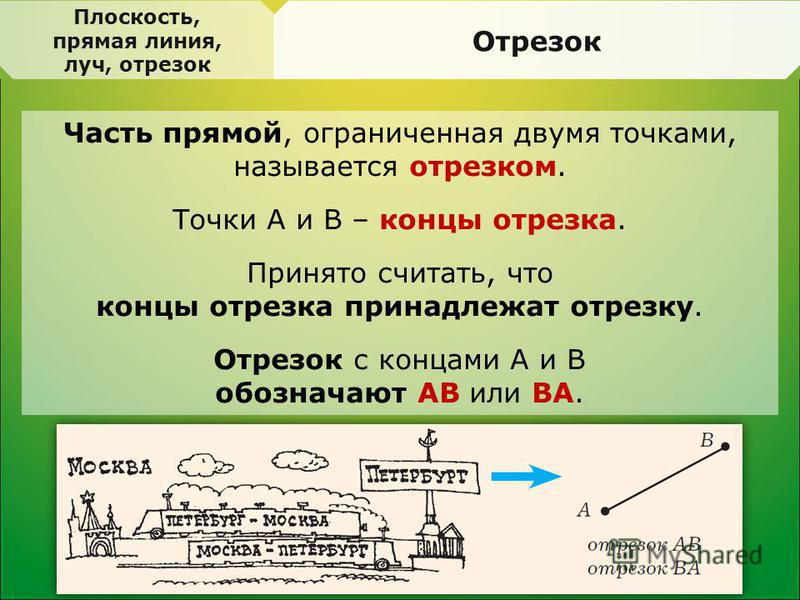
Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются.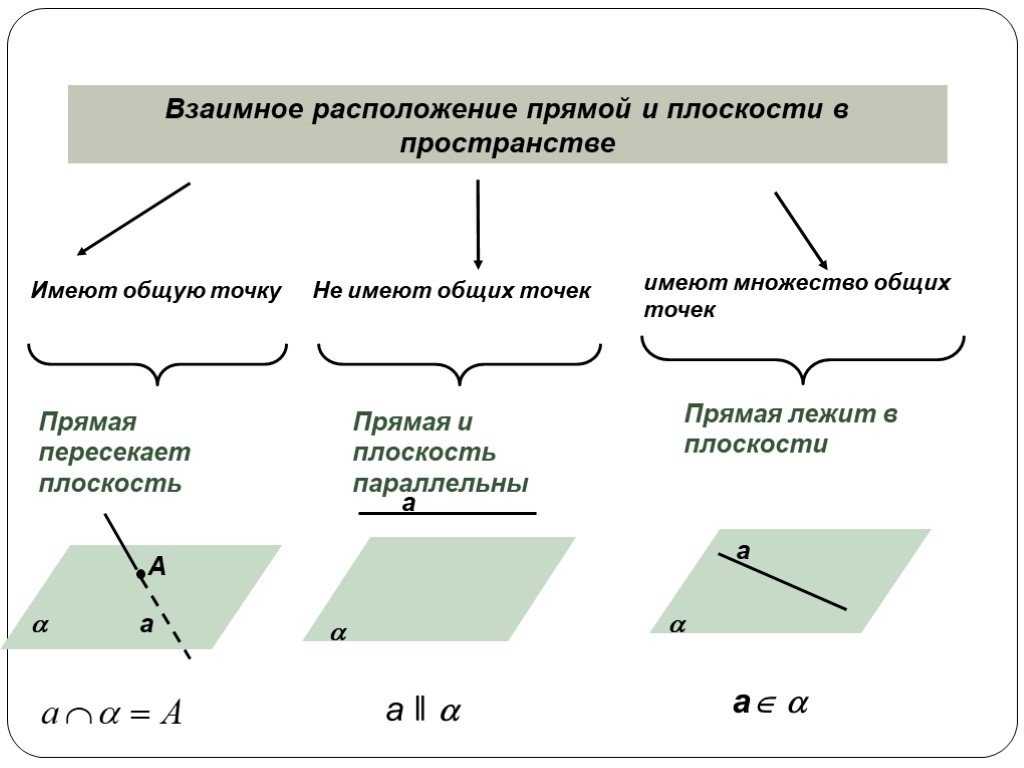

Рис. 5 Пересечение прямых

На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O, а прямые q и g не пересекаются.

Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q.

Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g, то станет понятно, что они тоже пересекаются.

Взаимное расположение точек и прямой, а также их обозначение, точно такое же, как и у всех линий вообще.

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч

Определение

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.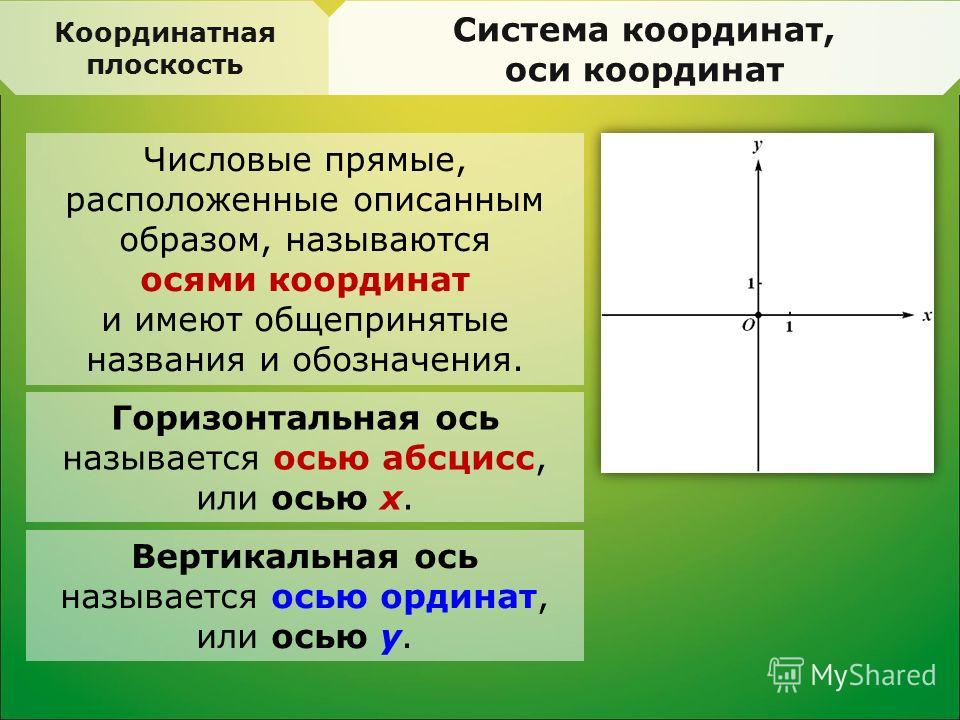

Рис. 6 Деление прямой линии точкой

На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O, которую называют началом луча.

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

• a – строчной (маленькая) буква латинского алфавита;
• OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.

Луч имеет второе название – полупрямая.

Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами, поскольку в соединенном виде они формируют одну прямую линию в точке их начала.

Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие, или говорят, что эти лучи совпадают.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

• CB и CH – дополнительные друг другу лучи,
• BC и BH – совпадающие лучи,
• HC и HB – совпадающие лучи.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.7 / 5. Количество оценок: 37

Оценок пока нет. Поставьте оценку первым.

Плоскость – правило, определение, виды

4.6

Средняя оценка: 4.6

Всего получено оценок: 134.

Обновлено 26 Февраля, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 134.

Обновлено 26 Февраля, 2021

Плоскость – это основная единица планиметрии. Для правильного восприятия сложных фигур, таких как, пирамида, конус или призма, необходимо понимать и, главное, представлять себе, что такое плоскость.

Определение плоскости

Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.

Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.

Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.

Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.

Способы задания плоскостей

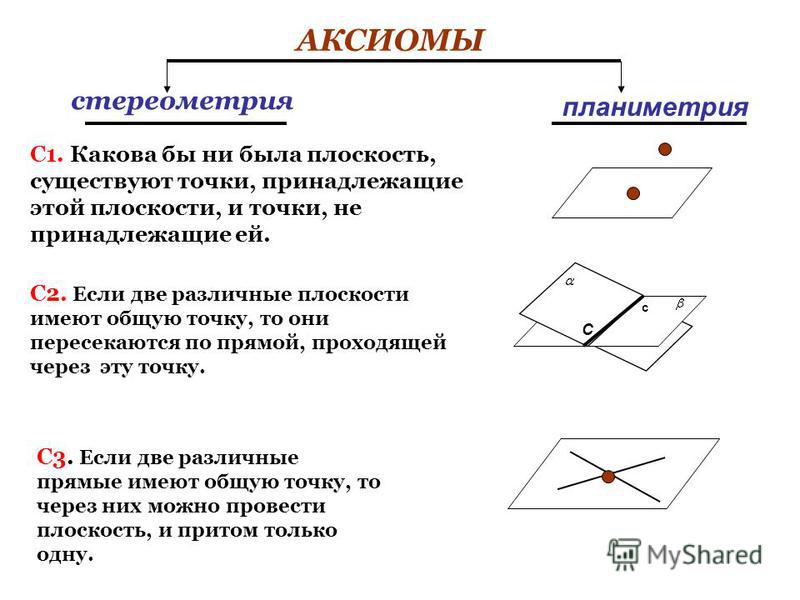
Плоскость может быть задана тремя точками, нележащими на одной прямой. Из этого утверждения следуют еще два варианта задания плоскостей. При этом специального знака плоскостей не существует.

Плоскость можно задать двумя пересекающимися прямыми, тогда одной точкой будет служить точка пересечения прямых, а двумя другими произвольные точки на одной и второй прямой.

Еще один вид это задание прямой и точкой, нележащей на этой прямой. По аналогии со вторым вариантам: одна точка уже есть и не лежит на прямой, а две других это произвольные точки имеющейся линии.

Рис. 1. Способы задания плоскостей.

Взаимное расположение прямой и плоскости

Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.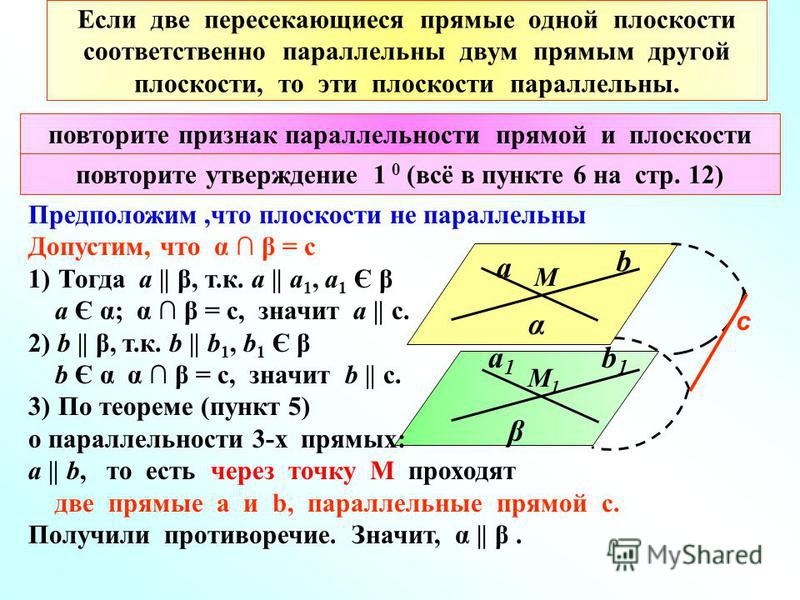

Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.

Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.

Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.

Рис. 2. Взаимное расположение прямой и плоскости.

Взаимное расположение плоскостей

Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.

Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.

Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.

Рис. 3. Расположение плоскостей.

Что мы узнали?

Мы дали определение и привели примеры плоскости. Выделили варианты пересечения прямой и плоскости и пересечения плоскостей. Привели несколько признаков, относящихся с плоскостям и разобрали все случаи существования плоскостей в пространстве.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Дария Петроченко

  3/5

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 134.

А какая ваша оценка?

Математика 5 класс | Образцы и координатная плоскость

Учащиеся знакомятся с координатной плоскостью и используют ее для представления положения объектов в пространстве, а также для представления закономерностей и реальных ситуаций.

Раздел 7

5-й класс

Краткое содержание раздела

В Разделе 7, последнем разделе года для 5 класса, учащиеся знакомятся с координатной плоскостью и используют ее для представления местоположения объектов в пространстве, а также как для представления шаблонов и реальных ситуаций.

Учащиеся согласовали числа и расстояние раньше, а именно с числовыми линиями. Ученики познакомились с числовыми рядами с целыми интервалами во 2 классе и использовали их для решения задач на сложение и вычитание, помогая установить связь между количеством и расстоянием (2.МД.5—6). Затем в 3 классе учащиеся построили числовые ряды с дробными интервалами, используя их для понимания идеи эквивалентности и сравнения дробей, снова связав это с идеей расстояния (3. NF.2). Например, две дроби, которые находились в одной и той же точке числовой прямой, были эквивалентны, а дробь, которая была дальше от 0, чем другая, была больше. Затем, в 4 классе, учащиеся научились складывать, вычитать и умножать дроби в простых случаях, используя числовую прямую в качестве представления, и они распространили это на все случаи, в том числе на простые случаи, связанные с делением дроби, в течение 5 класса (5.NF .1—7). Подготовка учащихся к этому разделу также связана с их обширной работой с шаблонами, начиная с детского сада с шаблонами в счетных последовательностях (K.CC.4c) и заканчивая работой в 4 классе с созданием и анализом числа или шаблона формы с учетом его правила (4 .ОА.3).

Таким образом, учащиеся начинают изучение модуля, думая о числовой прямой как способе представления расстояния в одном измерении, а затем видят полезность отрезка перпендикулярной линии для определения расстояния во втором измерении, позволяя любой точке в двумерном пространстве быть находится легко и точно (MP. 6). После большой практики определения координат точек, а также нанесения точек по заданным координатам с помощью координатных сеток различных интервалов и масштабов, учащиеся начинают рисовать линии и фигуры на координатной сетке, замечая простые закономерности в своих координатах. Затем, после того как учащиеся освоятся с координатной плоскостью как способом представления двухмерного пространства, они представляют реальные и математические ситуации, а также два числовых шаблона, графически изображая свои координаты. Это визуальное представление обеспечивает богатую интерпретацию этих контекстов (MP.2, MP.4).

Эта работа является важной частью «прогресса, который ведет к алгебре в средней школе» (6—7.RP, 6—8.EE, 8.F) (K–8 Publishers’ Criteria for the Common Core State Standards по математике, стр. 7). Затем это глубоко информирует студентов о работе на всех курсах средней школы. Таким образом, 5-й класс заканчивается дополнительным содержанием кластера, но это обозначение не должно умалять его значения в этом году и в последующие годы.

Темп: 14 учебных дней (12 уроков, 1 гибкий день, 1 контрольный день)

Fishtank Plus для математики

Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.

Узнать больше

Оценка

Следующие оценки сопровождают Раздел 7.

Предварительная часть

Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.

Промежуточный модуль

Предложите учащимся выполнить оценку промежуточного модуля после урока 7.

Послемодульный

Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.

• Постмодальная оценка

• Ключ к ответам после модульной оценки

• Руководство по анализу послемодульной оценки

  92F25A3F-8529-4314-9899-6EE68694E3D0

• Самооценка студентов после окончания обучения

Расширенный пакет оценивания

Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить способности учащихся с базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.

Скачать образец

Подготовка блока

Интеллектуальная подготовка

Рекомендации по подготовке к обучению этому разделу

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Интеллектуальная подготовка для всех разделов

• Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
• Выполните все целевые задачи и снабдите их комментариями с учетом «Сводки модуля» и «Основных сведений».
• Пройти итоговую оценку.

Основные понятия

Основные математические концепции, которые учащиеся поймут в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• Так же, как понимание числа и длины может быть применено в одном измерении с использованием числовой линии, числа и длины могут быть скоординированы в двух измерениях, чтобы понять расположение объектов в пространстве.
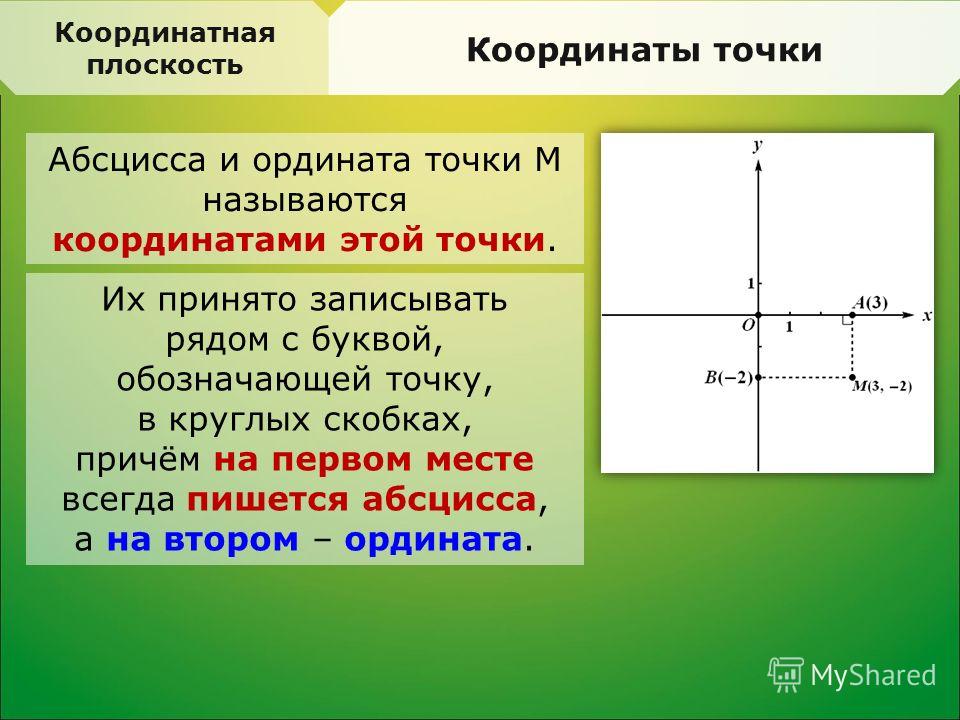
• Точку (2, 3) можно рассматривать двумя разными способами: (1) как указание «вправо 2, вверх 3» и (2) как точку, определяемую расстоянием 2 от оси y . и расстояние 3 от оси x . В этих двух интерпретациях цифра 2 связана с осью x (в первой интерпретации) и с осью y (во второй интерпретации).
• Точно так же, как отношения могут существовать между терминами в одном шаблоне, отношения могут существовать между соответствующими терминами в двух шаблонах. Это основа любого функционального понимания.
• Графические координатные точки, которые представляют реальную ситуацию или закономерности, могут помочь выявить тенденции и особенности, которые иначе было бы трудно идентифицировать.

Запас слов

Термины и обозначения, которые студенты изучают или используют в модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

ось, ось x, ось y

координатная плоскость

координатная пара

0 соответствующие термины x-координата, y-координата

заказанная пара

происхождение

срок

Чтобы увидеть весь словарный запас для модуля 7, просмотрите наш глоссарий лексики для 5-го класса.

Материалы

Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого занятия

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• Маркеры или мелки (по 3 на учащегося)
• Миллиметровая бумага (3 листа на учащегося). Если у вас недостаточно печатной миллиметровой бумаги, вы можете предоставить учащимся бумагу с дюймовой сеткой.
• Дополнительно: Миллиметровая бумага в четверть дюйма (3 на учащегося) — это необязательно, если у вас нет миллиметровой бумаги.

Модульная практика

Словесные задачи и упражнения на беглость речи

Получите доступ к ежедневным практикам со словесными задачами и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.

Предварительный просмотр

Узнать больше

Карта урока

Тема A: Знакомство с координатной плоскостью

Построить координатную плоскость и определить координаты заданных точек.

5.G.A.1

Построить координатную плоскость и нанести точки по заданным координатам.

5.G.A.1

Построить координатную плоскость с неединичными интервалами и использовать ее для построения и идентификации точек.

5.G.A.1

Определите интервал, необходимый для нанесения различных точек, и попрактикуйтесь в построении и идентификации точек на координатных сетках с различными осями.

5.G.A.1

Тема B: Рисование фигур и фигур в координатной плоскости

Нанесите горизонтальные и вертикальные линии на координатную плоскость и найдите закономерности в их координатах.

5.G.A.1
5.Г.А.2

Начертите параллельные линии на координатной плоскости.

5.G.A.1
5.Г.А.2

Рисование перпендикулярных линий на координатной плоскости.

5.G.A.1
5.Г.А.2

Рисование фигур на координатной плоскости.

5.G.A.1
5.Г.А.2

Нарисуйте симметричные фигуры на координатной плоскости.

5.G.A.1
5.Г.А.2

Тема C: Реальные проблемы и закономерности на координатной плоскости

Решайте реальные проблемы, отображая информацию, представленную в таблице, в координатной плоскости и интерпретируйте значения координат точек в контексте ситуации.

5.Г.А.2

Решайте реальные проблемы, отображая в виде графика информацию, представленную в виде описания ситуации в координатной плоскости, и интерпретируйте значения координат точек в контексте ситуации.

5.Г.А.2
5.OA.B.3

Создайте два числовых шаблона, используя два заданных правила, нанесите точки и определите отношения между соответствующими терминами.

5.OA.B.3

Общие базовые стандарты

Ключ

Основной кластер

Вспомогательный кластер

Дополнительный кластер

Основные стандарты

Стандарты контента, описанные в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Геометрия

• 5. Г.А.1

  — Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии, и заданной точкой на плоскости, расположенной с помощью упорядоченной пары. чисел, называемых его координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).
  

• 5.Г.А.2

  — Представлять реальный мир и математические задачи, изображая точки в первом квадранте координатной плоскости и интерпретируя значения координат точек в контексте ситуации.
  

Операции и алгебраическое мышление

• 5. ОА.Б.3

  — Сгенерируйте два числовых шаблона, используя два заданных правила. Определите очевидные отношения между соответствующими терминами. Сформируйте упорядоченные пары, состоящие из соответствующих терминов из двух шаблонов, и отобразите упорядоченные пары на координатной плоскости.
  Например, учитывая правило «Добавить 3» и начальный номер 0, а также правило «Добавить 6» и начальный номер 0, сгенерируйте термины в результирующих последовательностях и обратите внимание, что термины в одной последовательности в два раза больше соответствующих термины в другой последовательности. Объясните неформально, почему это так.

Основополагающие стандарты

Стандарты, описанные в предыдущих модулях или классах, которые являются важной основой для текущего модуля

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Геометрия

• 4.Г.А.1

• 4. Г.А.3

• 5.RUS4

Измерения и данные

• 2.MD.B.6

Числа и операции — дроби

• 3.NF.A.2

Операции и алгебраическое мышление

• 4.OA.C.5

Будущие стандарты

Стандарты будущих классов или разделы, связанные с содержанием данного раздела

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Выражения и уравнения

• 6.EE.C.9

Геометрия

• 6.Г.А.3

Соотношения и отношения пропорциональности

• 6.РП.А.3

Система счисления

• 6. Н.С.6

• 6.NS.C.8

Стандарты математической практики

• CCSS.MATH.PRACTICE.MP1
  — Разбираться в проблемах и настойчиво решать их.

• CCSS.MATH.PRACTICE.MP2
  — Рассуждайте абстрактно и количественно.

• CCSS.MATH.PRACTICE.MP3
  — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.

• CCSS.MATH.PRACTICE.MP4
  — Модель с математикой.

• CCSS.MATH.PRACTICE.MP5
  — Стратегически используйте соответствующие инструменты.

• CCSS.MATH.PRACTICE.MP6
  — Следите за точностью.

• CCSS.MATH.PRACTICE.MP7
  — Ищите и используйте структуру.

• CCSS.MATH.PRACTICE.MP8
  — Ищите и выражайте закономерность в повторяющихся рассуждениях.

значок/стрелка/право/крупная копия

Модуль 6

Умножение и деление десятичных дробей

Планы уроков — Координатная плоскость

w3.org/1999/xhtml» cellspacing=»0″> Планы уроков Нажмите на ссылки ниже, чтобы прочитать планы урока.   – День 1. Переходим к делу Просмотр Учащиеся узнают о Рене Декарте (основателе аналитической геометрии) и связи между декартовой системой координат и математикой. 13 апр. 2013 г., 15:13 Кендра Риг – День 2 — Шпионы Просмотр Видео-знакомство с координатной сеткой и интерактивная игра для закрепления понятий, изученных в видео. 13 апр. 2013 г., 15:17 Кендра Риг – День 3. Построение графика в квадранте 1 на координатной плоскости Вид Учащиеся знакомятся с построением графиков на координатной плоскости в первом квадранте с использованием координат (x, y). Эта деятельность CYBERCHASE мотивирована видеоклипом, в котором CyberSquad потерян, а ориентиры неоднозначны. Они используют сетку карты для построения системы координат с использованием букв и цифр. 13 апр. 2013 г., 15:26 Кендра Риг – День 4. В поисках пути Просмотр Учащиеся исследуют двухмерное пространство с помощью упражнения, в котором они перемещаются по координатной плоскости. Студенты используют апплет Simple Plot на компьютере для ввода упорядоченных пар, и компьютер рисует их для студента. В качестве проверки понимания учащиеся могут использовать апплет игры «Координация», который дает учащимся баллы, а учащиеся вводят координаты и проверяют, чтобы убедиться, что они верны. 13 апр. 2013 г., 15:28 Кендра Риг – День 5 — Сопоставьте мой шедевр Просмотр Учащиеся начертят на сетке точки, соответствующие заданным им упорядоченным парам. Если все сделано правильно, точки сформируют слово. 13 апр. 2013 г., 15:39 Кендра Риг – День 6. Опишите конструкцию Посмотреть На этом уроке учащиеся рассмотрят точки построения и оси надписей. Студенты генерируют набор случайных точек, расположенных в первом квадранте. ➜