Содержание
Сравнение предметов по форме и цвету | План-конспект урока по математике (1 класс):
Тема урока: «Сравнение предметов по форме и цвету»
Цель: формирование умения сравнивать объекты по общим признакам – форме и цвету.
Задачи:
предметные:
— формировать умения различать предметы по форме и цвету, распознавать и изображать геометрические фигуры;
— способствовать овладению основами пространственного воображения, использованию математических представлений для описания окружающих предметов;
— создавать условия для понимания математики, как науки, необходимой в жизни
метапредметные:
— способствовать овладению логическими действиями сравнения, анализа, сопоставления, установлению причинно- следственных связей;
— развивать навыки самоанализа и взаимоанализа успешности участия в учебном диалоге;
— развивать устную речь учащихся, умение конструировать монологические высказывания;
— разъяснять необходимость знания дорожных знаков и соблюдения правил безопасного поведения на дорогах;
— развивать мелкую моторику руки первоклассников;
— содействовать созданию доброжелательных отношений в классе
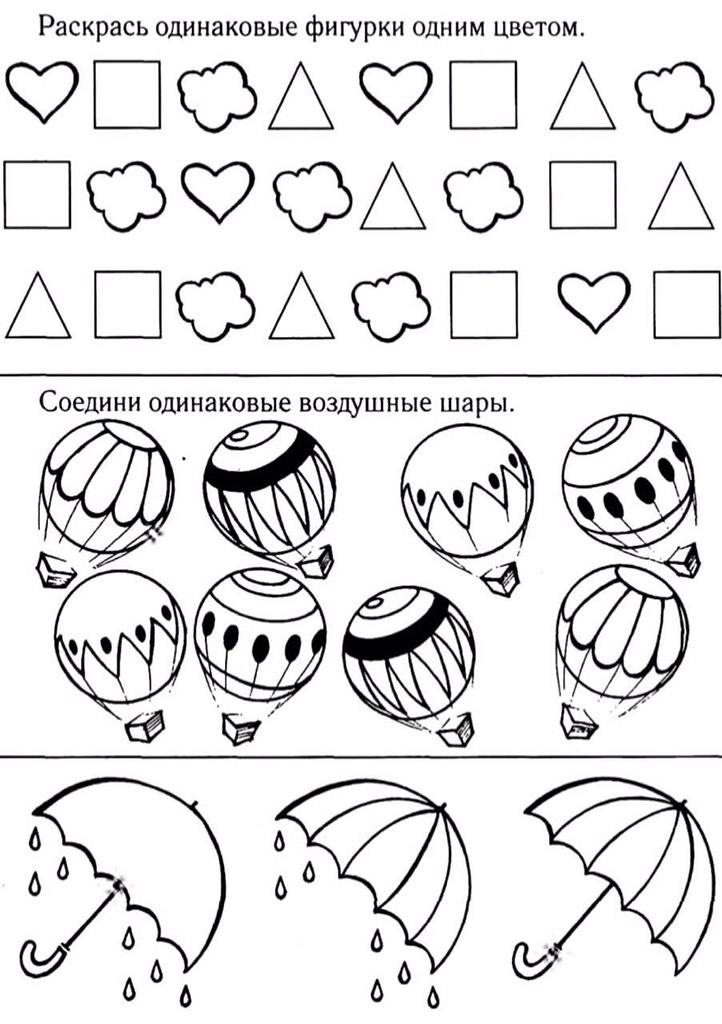
Оборудование: — карточки — «закладки» на доску /Приложение 1/;
— раздаточный геометрический материал в конвертах (один на парту) /Приложение 2/;
— изображение дорожных знаков /Приложение 3/
-учебники, рабочие тетради.
Ход урока.
- Организационный момент. Эмоциональный настрой.
Начинаем точно в срок
Математики урок.
Чтобы многое узнать,
Нужно думать, размышлять
И друг другу помогать!
Но нельзя, дружок, зевать!
- Подготовка к изучению новой темы.
1.- Ответьте на вопрос.
— У Алеши есть старшая сестра Ирина, а у Ирины есть младший брат. Сколько детей у их мамы?
2. -К учебному году Ира и Алеша изготовили закладки и украсили их узорами. Вот какие закладки получились. (На доску вывешиваются две полоски с геометрическими фигурами) / Приложение 1/
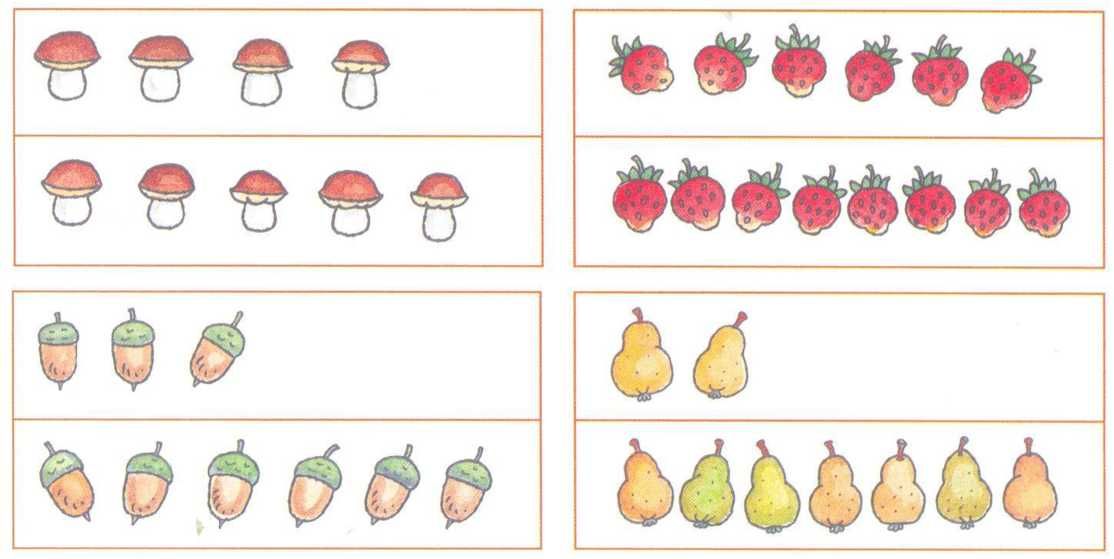
— Сколько геометрических фигур использовала Ирина? А сколько Алексей? Что вы можете сказать о количестве фигур, которые использовали ребята? ( Количество фигур у них одинаково; у каждого по 5 фигур на закладке, вместе фигур 10 и т.п.)
— Какие геометрические фигуры использовали ребята для составления узора?
— Чем похожи узоры сестры и брата?
— Чем они отличаются?
- Тема урока.

— Ребята, как вы думаете, чему мы будем учиться сегодня на уроке?
(Ответы детей)
— Верно, сегодня на уроке мы будем учиться сравнивать предметы по форме и цвету.
- Изучение нового материала.
- Работа по учебнику. Задание 5(с.8).
– Откройте учебники по закладке на странице 8. Надпись внизу страницы. (Написать на доске цифру)
– Посмотрите на рисунок вверху страницы, справа от цифры 5.
Что вы видите на рисунке? (Мы видим детские песочницы)
— Сколько песочниц на рисунке? (Четыре)
— Сравните верхние песочницы. Чем они похожи? (Они похожи цветом (одинаковые по цвету), обе песочницы розовые)
— Чем различаются? (Песочницы различаются по форме, одна — круглая, а вторая — квадратная, в одной мало песка, а в другой — много)
— В какой верхней песочнице много песка? В какой мало? (Много песка в левой песочнице, а мало – в правой)
— Молодцы! А теперь сравните нижние песочницы по форме и по количеству песка в них. (Эти песочницы разные и по форме и по количеству песка)
(Эти песочницы разные и по форме и по количеству песка)
— Сравните песочницы, расположенные справа. (Они одинаковые по форме и по количеству песка, но разные по цвету)
— Теперь сравните песочницы, расположенные слева. (Эти песочницы одинаковые по форме, но разные по цвету и количеству песка в них)
— А сколько на рисунке круглых песочниц? ( Две)
— Сколько квадратных? (Тоже две)
— Что можно сказать о количестве круглых и квадратных песочниц? (Их одинаково)
- Работа в тетрадях.
— Нарисуйте в тетради столько кругов, сколько на странице круглых песочниц, и столько квадратов, сколько квадратных песочниц.
( Самостоятельная работа с взаимопроверкой)
- Практическая работа в парах.
— А вы любите играть в песочнице? А какие игрушки вы используете в таких играх? ( Лопатка, совок, формочки для куличиков, игрушечные грузовики, другие машинки и т.д.)
-Как называются машины, предназначенные для перевозки песка и щебня? (Грузовики, самосвалы). Сейчас мы составим такие грузовики из геометрических фигур.
Сейчас мы составим такие грузовики из геометрических фигур.
— Перед вами конверты, откройте их./Приложение 2/. Перечислите геометрические фигуры, какие вы видите. (Круги, квадраты, прямоугольники).
Мы будем работать сообща. Напомните правила работы в парах. (Советоваться с товарищем, спокойно рассуждать, не повышая голоса, принимать общее решение)
— Внимательно послушайте задание. Выложите два грузовика так, чтобы они состояли из одинаковых по форме деталей, но разных по цвету.
— Расскажите, как вы выполняли эту работу? (Ответы детей)
— Почему выбрали такие геометрические фигуры? (Ответы детей)
— Можно ли сказать, что ваши грузовики получились одинаковые? (Нет, у них разного цвета детали, хотя и одинаковые по форме)
– Молодцы, вы очень хорошо работали! Какие замечательные грузовики получились! Давайте немножко отдохнем.
Физкультминутка
Самосвалом я зовусь: ( Шаг на месте)
Сам я сваливаю груз. (Наклоны вперед- назад)
Разгружать меня не надо, (Наклоны влево — вправо)
Все такой машине рады. (Руки в стороны, вверх- вдох.
(Руки в стороны, вверх- вдох.
Руки в стороны, вниз- выдох)
- Работа по учебнику (продолжение).
Задание 6(с.8).
— Посмотрите на задание под номером 6. (Цифра записывается на доске)
Какие из нарисованных предметов могут быть связаны с грузовиком? Почему вам так кажется? (Варианты ответов: колесо – это деталь машины; подсолнух, часы и шляпа круглые как колеса; дорожный знак вдоль дорог, где ездят настоящие машины и т.п.)
— Как называется изображенный дорожный знак? («Пешеходный переход» (знак для водителей)- В случае затруднения учитель сам дает ответ).
— Зачем нужны дорожные знаки? (Ответы детей)
-А как выглядит знак «Пешеходный переход» — знак для пешеходов? (Ответы детей) Что он означает? (Ответы детей) / Приложение 3/
— Проверим. (Учитель вывешивает на доску оба знака для сравнения). Назовите сходства и различия этих знаков, не забывая при этом о теме сегодняшнего урока. (Ответы детей).
— Какое значение имеет цвет и форма в дорожном знаке? (Ответы детей).
– Прочитаем задание в учебнике. (Хорошо читающий ученик читает вслух)
— На каких предметах можно увидеть квадрат, круг, треугольник? Назовите эти предметы. (Ответы детей)
Молодцы! Работаем дальше на следующей странице.
- Задание 7(с.9).
— Сравните рисунки. Найдите сходства и различия в рисунках. (Ответы детей)
— Что значит сравнивать предметы? Объясните. (Сравнивать предметы — это находить, чем они похожи и чем различаются и т.п)
- Отгадайте загадку
Кинешь в речку — не утонет,
Бьёшь о стенку — он не стонет,
Будешь оземь кидать —
Станет кверху летать. (Мяч)
— Почему я выбрала такую загадку? Кто догадался? (Потому что на картинке мальчик играет мячиком; мяч — тоже, как и машинка, игрушка и т.п.)
— Давайте отдохнем и представим, что мы веселые мячики.
Физкультминутка
(Присесть, прыгать на согнутых в коленях ногах, «на корточках», в такт читаемому стихотворению)
Мой веселый, звонкий мяч,
Ты куда пустился вскачь?
Желтый, красный, голубой —
Не угнаться за тобой.
— О каком признаке предметов говорится в этом стихотворении? (О цвете)
-Какие известные вам цвета мы на уроке еще не называли? (Ответы детей)
— Замечательно мы отдохнули и продолжаем дальше!
- Задание 8. (с.9)
— Посмотрите на классную доску.
-Что расположено слева от тебя? Что справа?
— Есть ли в школьном кабинете предметы, которые различаются только по форме; только по цвету; по форме и по цвету? (Ответы детей)
- Разминка для глаз
— Подойдем к окну и посмотрим. Какие схожие по форме предметы вы видите? Назовите предметы, схожие по цвету? А какие предметы одинаковые и по форме и по цвету одновременно? (Ответы детей)
- Работа в тетради
— Глазки наши отдохнули, пальчики отдохнули, пора бы им потрудиться.
— В тетради нарисуйте палочки так, как показано в учебнике (Задание 9(с.9))
- Работа над развитием устной речи.
Задание 10 (с.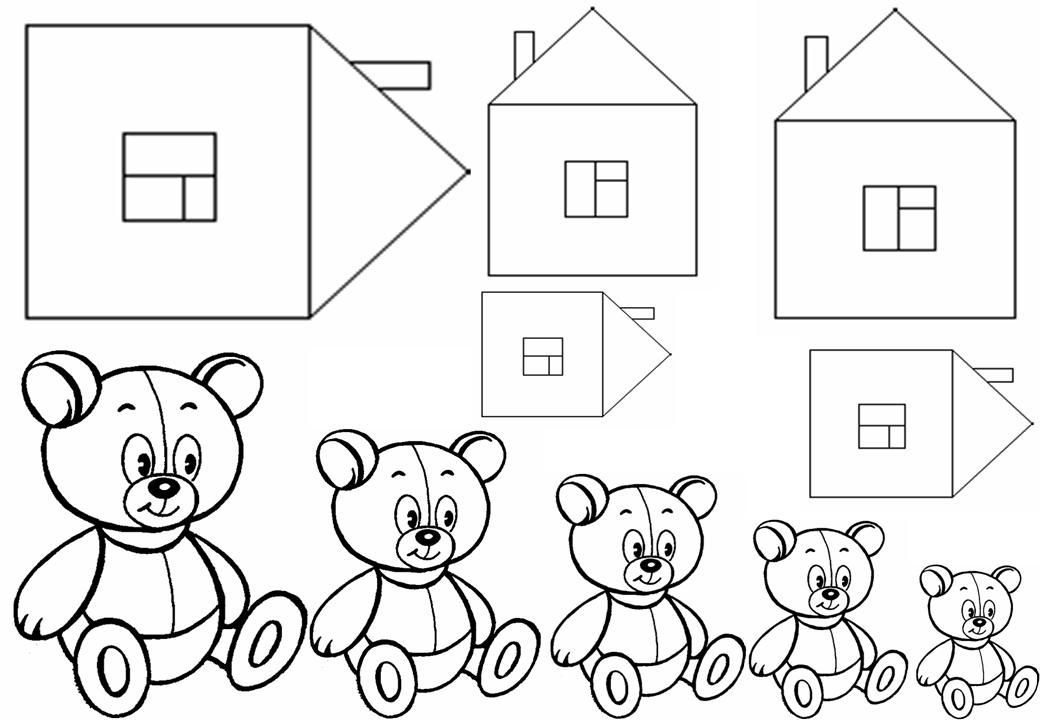 9).
9).
— Рассмотрите рисунок. Что было сначала? Что потом?
— Составьте рассказ по картинкам. Расскажите товарищу. (Работа в парах)
-Кто хочет выступить со своим рассказом? (Рассказы детей по желанию)
- Рефлексия. Итог урока.
— Ребята, вы сегодня хорошо поработали.
— Какие открытия мы сегодня сделали на уроке? О чем бы захотелось рассказать дома маме и папе?
— Какое задание было для вас самым интересным? Какое задание показалось трудным? (Ответы детей)
— Если вам на уроке было легко работать, поднимите синий квадрат, если были затруднения – красный прямоугольник.
— Спасибо за урок!
Приложение 1.
Приложение 2 /примерный вариант/
По 2шт.
По 2шт.
По 2шт.
По 2шт.
Приложение 3
«Пешеходный переход» — знак для пешехода
«Пешеходный переход» — знак для водителя
Урок математики на тему «Понятия «длиннее», «короче», «одинаковые по длине», 1 класс
В ходе практической работы и наблюдений научить сравнивать длину предметов разными способами.
— Уточнение и формирование отношений «длиннее», «короче», «одинаковые по длине»;
— Воспитывать чувство товарищества, умение выслушивать ответы товарищей и дополнить по необходимости;
— проблемный (создание проблемной ситуации, которые помогли детям в открытии новых знаний).
— частично – поисковый (учим детей наблюдать, анализировать, сравнивать, делать выводы и обобщения под руководством учителя),
Учебник математики для 1 класса под редакцией Моро М.И., Волкова С.И., ленточки разного цвета и разной длины, наборы полосок разной длины (для работы в парах), наборы геометрических фигур, наборы цифр и знаков, цветные карандаши.
Исходный уровень знаний, умений и навыков, необходимых для проведения урока по данной теме:
Знакомы с понятиями «больше», «меньше», «столько же»; различают понятия «число» и «цифра»; знакомы с числами от 1 до 4, умеют писать цифры 1, 2, 3, 4. Работают в парах, в группах.
Этапы урока | Деятельность учителя | Деятельность обучающихся | Какие УУД формируются | |
Организационный момент (1минута) | -Звенит звонок – начинается урок. — Ребята, а какое настроение у вас сегодня? Я надеюсь , что и в конце урока у вас будет такое хорошее настроение. Сегодня на урок пришла сказка. А главного героя узнаете из загадки: Он испёкся в русской печке, Покатился за крылечко. У него румяный бок. Это вкусный…(Колобок) — Давайте уважим Колобка, вспомним его сказку. Кто написал сказку? Значит она – народная. Итак, кто начнёт? | Обучающиеся повторяют за учителем. Вспоминают сказку. | Организовать направленное внимание на начало урока. Личностные УУД: Внимание,уважение к окружающим. Регулятивные УУД: Саморегуляция. | |
2.Целеполагание (1 минута) | А вот по этой дорожке покатился Колобок . — Кого встретил Колобок первым? ( вывешиваю Зайца). –Колобок, Колобок ,я приготовил разные задания. Если справишься-не буду есть тебя. Ребята, поможем Колобку? | Регулятивные УУД: Определять и формулировать цель деятельности на уроке с помощью учителя. Учиться высказывать свое предположение (версию) на основе работы с иллюстрацией учебника. Понимать учебную задачу урока и стремиться её выполнить. | ||
Проверка изученных тем (8 минут) | 1. Устный счёт. Счёт от 1 до 10 в прямом и обратном порядке. Счёт с любого числа. Назови соседей числа 5;8, 12 Назови число, следующее за числом 6;9,15 Назови число предыдущее 4; 7,11 Какой сегодня день недели. Поднимите правую руку. Покажите левое ушко. Поднимите глазки вверх. Опустите голову вниз. Молодцы! Справились с первым заданием. Зайчик очень любит изучать геометрические фигуры и приготовил сложное задание. Справитесь? 2.Работа с геометрическим набором. Положите красный треугольник. С права – 2 желтых квадрата, а слева- красный квадрат.
Сколько фигур справа от красного треугольника? (3) Сколько кружков слева от красного треугольника? (2) Сколько всего кружков? (2) Сколько треугольников? (1) Сколько нужно еще положить треугольников, чтобы их стало столько же, сколько кружков? Квадратов? 3. -У меня , говорит Зайчик, есть 2 пустых корзинки. Как мне разложить в них 2 яблока? 3 гриба? 4 морковки? (ученики показывают, выходя к доске). 4.Пропедевтика темы «Задача». Приготовьте свои счетные наборы, они нам сейчас потребуются. На экране картинка: (по презентации) Составьте рассказ о том, что вы сейчас увидели. Как записать ваш рассказ математическим зыком? (2+1) Возьмите нужные знаки их счетных наборов и выложите эту запись у себя на парте. (проверим по презентации) Прочитайте это выражение разными способами. Следующая задача. (5-2) | Считают хором Фронтальная работа Фронтальная работа Работают с наборами геометрических фигур. Выходят к доске, предлагают решение Выкладывают выражения цифрами и знаками.
| Регулятивные: Целеполагание, контроль, саморегуляция. Учиться работать по предложенному учителем плану. Учиться совместно с учителем и другими учениками давать эмоциональную оценку деятельности класса на уроке. Учиться технологии оценивания образовательных достижений (учебных успехов). | |
3.Физкультминутка (1 минута) | — Молодцы, справились со всеми заданиями Зайчика. Покатился Колобок дальше. Давайте и мы пойдём по его дорожке. ( разминка по презентации ) | Повторяют движения | Личностные: Самовыражение. Здоровьесбережение. | |
4.Актуализация знаний (3 минуты) | Кого потом встретил Зайка? Волк говорит Зайцу: — Я не буду тебя есть, если ты поможешь разобраться в одном вопросе. Поможем? (достаю 2 ленты у Волка) — Посмотрите у меня в руках две ленточки. (Учитель показывает две ленточки разного цвета и разной длины ,длина лент не должна сильно отличаться.) — Которая из ленточек длиннее? Уверены? Можно ли сразу сделать вывод, сравнивая на глаз? | Дети на глаз определяют, которая ленточка длиннее, высказывают свои предположения. | Коммуникативные: Слушать, читать, говорить, перерабатывать информацию на основе анализа и синтеза. Познавательные: группировать, классифицировать, сравнивать, описывать, доказывать. . Личностные: Выполнение моральных норм в отношении других учителей, своих сверстников. | |
5.Работа по новой теме урока. 1.Организация восприятия и осмысления новой информации. (3 минуты) 2.Первичная проверка понимания. ( 5 минуты) | — Как можно проверить, правильно ли вы ответили? (Нужно приложить одну веревочку к другой.) (Учитель прикладывает ленточки друг к другу не совмещая края ). — Какая ленточка длиннее? Правильно ли я сделала? Как надо приложить? Давайте вы попробуете. — Теперь мы можем ответить на вопрос — какая ленточка длиннее? Так что мы делали? Как сравнивали? (прикладывали) А что можно сделать , чтобы ленточки стали одинаковые по длине? У нас сейчас произойдёт маленькое волшебство ( ножницами отрезаю, ленты становятся равными ). — Какие слова мы использовали при сравнении длины ленточек? — Эти слова будут сегодня главными на уроке.- 2.Практическая работа в парах Следующее задание, которое я вам предложу- говорит Волк- вы будете выполнять в парах.
Возьмите конверт. Сравните полоски бумаги одним из изученных нами способов – наложением или «на глаз». — Поднимите самую длинную полоску. Какая полоска оказалась самая короткая? Что можете сказать о жёлтых полосках? А одинаковые ли они во всём? ( разные по ширине) .А влияет ли это на длину? -Поработаем в Печатной рабочей тетради. Открываем на с.12. Читаем задание. Сначала обсудите в паре. — Какая полоска оказалась самая длинная? — Кто выполнил правильно -погладьте себя-молодцы! | Учащиеся предлагают разные способы, останавливаемся на варианте – приложить друг к другу. Учащиеся путём рассуждений должны прийти к выводу, что учитель неправильно приложил ленточки друг к другу. Надо совместить один конец ленточки с концом второй ленточки . Работа в парах. Выполняют задание в рабочей тетради. | Коммуникативные: слушать, читать, говорить, перерабатывать информацию на основе анализа и синтеза. Познавательные: Добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке, выполнять индивидуальные задания. Перерабатывать полученную информацию: делать выводы в результате совместной работы всего класса. Перерабатывать полученную информацию: сравнивать и группировать предметы и их образы. | |
6.Подвижная физкультминутка. (1 минута) | Сколько точек будет в круге, Столько раз поднимем руки. Сколько ёлочек зелёных, Столько сделаем наклонов. Приседаем столько раз, Сколько бабочек у нас. А притопнем столько раз, Сколько ёжиков у нас. А прихлопнем столько раз, Сколько белочек у нас.- | Считают и выполняют задания. | Личностные: Самовыражение. Здоровьесбережение. | |
7.Организация усвоения способов деятельности путём воспроизведения информации и упражнений в её применении. ( 7 минут) | — Кто был следующий герой? А что это у Медведя в лапах? Как вы думаете, откуда будут задания? 1.Работа по учебнику. -Откройте на стр. 32 Рассмотрите рисунок. Что делают ребята? — Давайте по рисунку выполним задания. Вас просят сравнить «на глаз» какой поводок длиннее, какой короче; чей хвост длиннее; чьи уши короче; какая лавочка длиннее. — Но сначала скажите, как вы понимаете «сравнить на глаз»? — Когда можно сравнить на глаз? Ответьте на вопросы. (При необходимости учитель повторит вопросы) — О чём ещё можно спросить, что длиннее, что короче? — Как мы сравнивали длину этих предметов? — Рассмотрите следующий рисунок. — Сравните ремни по длине. Какой ремень длиннее? — Какой ремень короче? — Сравните ремни по ширине. Какой ремень шире, какой уже? | — Выгуливают собак. Дрессируют их на площадке. — Сравнить, не измеряя, не накладывая. — Когда явно видно, что длиннее, что короче. Дети отвечают на вопросы, сравнивая предметы «на глаз». — О шарфах, о собаках, о горках и т.д. — «На глаз». — Приложили один к другому. — Жёлтый. — Красный — Жёлтый ремень шире, красный ремень уже. | Коммуникативные: Учиться выполнять различные роли в группе (лидера, исполнителя, критика; осваивать ролевые игры). Работать в группах и парах. Составлять небольшой рассказ на заданную тему. | |
8. (3 минуты) | Молодцы! Вы очень хорошо поработали. -Кого встретил ещё Колобок? Лиса самая хитрая и приготовила Колобку сложное испытание. Поможем? Подумайте -у кого какая по длине должна быть скакалка? (работа по листочкам) Проверьте ( по экрану). Так у кого самая длинная? Почему? | Выполняют задание. | Личностные: Учиться выполнять различные роли в группе (лидера, исполнителя, критика; осваивать ролевые игры). Работать в группах и парах. Составлять небольшой рассказ на заданную тему. Познавательные: Перерабатывать полученную информацию: делать выводы в результате совместной работы всего класса. | |
9. Итог урока. Рефлексия. (2 минуты) | А теперь подведем итоги нашей работы. -Так ли закончилась сказка как у нас? Почему? Потому что у нас была математическая сказка! -Чему вы научились на уроке? С какими понятиями познакомились? -Какие способы использовали для сравнения длины? (на глаз, приложение, наложение) А теперь сделаем так: *те дети, которым было сегодня интересно на уроке и все у них получалось- поднимите руки . *у кого что-то не получалось, было трудно, но они все равно очень старались — поднимите руки . А теперь похлопайте себе- вы справились со всеми заданиями героев! Колобок очень благодарен вам за урок и на память оставляет вам подарок! (закладки с Колобком) — Спасибо за работу. Урок окончен. | Учащиеся проговаривают, что им понравилось, в чем были трудности, что нужно еще повторить. | Коммуникативные: Учиться совместно с учителем и другими учениками давать эмоциональную оценку деятельности класса на уроке. Регулятивные: Учиться технологии оценивания образовательных достижений (учебных успехов). |
Что эквивалентно? Определение, применение, пример, факты
Определение эквивалента
Значение термина «эквивалент» обычно относится к двум числам, выражениям или величинам с одинаковым значением. Есть много способов выразить эквивалентную величину — ее можно обозначить как чертой, так и эквивалентным символом. Дети находят эту тему очень интересной по нескольким причинам, поскольку они могут относиться к ней в своей повседневной жизни.
Эквивалент может также означать некоторую общую или логическую эквивалентность между различными значениями или количествами. Эквивалентность похожа, но не то же самое, что равенство.
Что означает эквивалент в математике?
Есть два способа определить эквивалент в математике. Это связано с тем, что термин «эквивалент» в математической теории — это понятие, имеющее несколько значений. Эквивалентность означает, что разные термины и выражения с одинаковым значением считаются равными в математической форме.
Эквивалентность означает, что разные термины и выражения с одинаковым значением считаются равными в математической форме.
Равно и равно
В математике эквивалент отличается от равного. Равный означает одинаковый во всех аспектах, тогда как эквивалентный означает подобный, но не идентичный.
Например, говорят, что 2 равно 2, но эквивалентно 1 + 1.
Проще говоря, мы можем сказать, что две вещи или количества равны, когда они точно такие же, как ½ равно ½, но ½ равно эквивалентно 2/4, поскольку они представляют одно и то же значение.
Эквивалентные выражения
Два математических выражения называются эквивалентными, если их решение дает один и тот же результат.
Например, , давайте решим следующие числовые выражения: 9{2}$ ÷ 4 также эквивалентны, так как оба могут быть упрощены до 4.
Эквивалентные дроби
Две дроби эквивалентны, если значение, пропорция или количество, которые они представляют, одинаковы.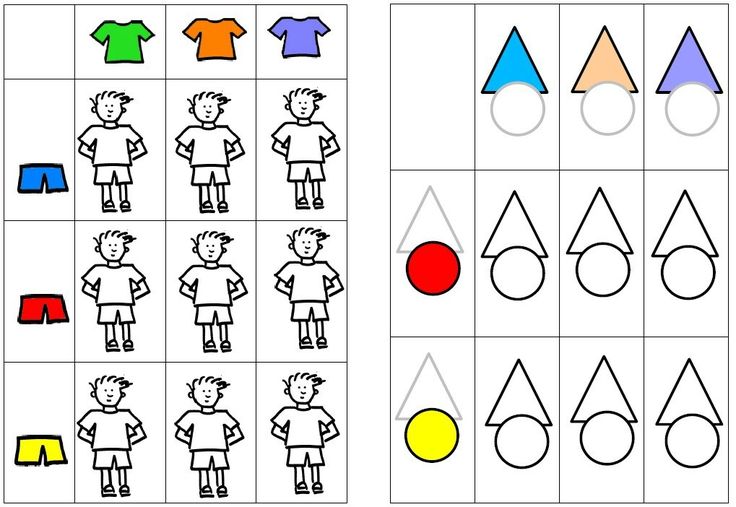 Равные дроби могут иметь разные числители и знаменатели.
Равные дроби могут иметь разные числители и знаменатели.
Например: $\frac{1}{2}$ = $\frac{2}{4}$ = $\frac{3}{6}$ = $\frac{4}{8}$
Эквивалентные отношения
Эквивалентные отношения — это отношения, которые могут выражать аналогичные или одинаковые отношения между числами или значениями.
Они похожи по соотношению и одинаково по стоимости. Эти отношения можно умножать или делить на их общие множители, что упрощает их. Эквивалентные отношения имеют разные числа в разных формах, но их отношение отражается только их конечным значением.
Например, 1:2 и 2:4 являются эквивалентными соотношениями.
Application
Использование эквивалентного символа (в виде трех полос) часто используется в программировании Unicode для компьютеров, а также в булевой алгебре. Диаграммы Венна используют концепцию логической эквивалентности для установления связи между двумя алгебраическими выражениями и функциями. Понятие эквивалентности также используется при объяснении структурного сходства между химическими соединениями.
Решенные примеры
Пример 1. Две дроби, $\frac{3}{5}$ и $\frac{6}{x}$, эквивалентны. Найдите значение x .
Решение : Дано, $\frac{3}{5}$ = $\frac{6}{x}$
Мы знаем, что эквивалентные дроби можно получить, умножив числитель и знаменатель на одно и то же число. . Итак, $\frac{3}{5}$ = $\frac{6}{10}$.
Следовательно, x = 10.
Пример 2: Проверить, эквивалентно ли 7 × 6 + 66 ÷ 11 – 5 × 2 7 × 3 + 24 ÷ 2 + 9× 3 или нет.
Решение: Чтобы проверить эквивалентность обоих выражений, решите и найдите окончательные значения.
7 × 6 + 66 ÷ 11 – 5 × 2
= 42 + 6 – 10
= 38
7 × 3 + 24 ÷ 2 + 9 × 3
38 ≠ 60
Итак, данные выражения не эквивалентны друг другу.
Пример 3: Являются ли $\frac{4}{5}$ и $\frac{16}{20}$ эквивалентными дробями?
Решение:
$\frac{4\times 4}{5\times 4}$ = $\frac{16}{20}$
Если умножить числитель и знаменатель $\frac{4} {5}$ на 4, получаем $\frac{16}{20}$.
Итак, данные дроби равнозначны.
Практические задачи
1 Выберите дроби, эквивалентные $\frac{5}{3}$, из списка дробей, показанного ниже.$\frac{4}{8}$ $\frac{10}{6}$ $\frac{9}{24}$ $\frac{15}{12}$ Правильный ответ: $\frac{10}{6}$ 2 Выберите дробь, эквивалентную пяти шестым$\frac{6}{5}$ $\frac{5}{6}$ $\frac{25}{30}$ $\frac{30}{25}$ Правильный ответ: $\frac{25}{30}$ 3 Две дроби $\frac{4}{15}$ и $\frac{12}{x}$ эквивалентны. Найдите значение х.12 15 45 60 Правильный ответ: 45 |
Заключение :
Мы узнали об эквиваленте и его свойствах и свойствах на разных примерах. Мы также решили несколько задач, которые помогли нам понять концепцию эквивалента. Надеюсь, это поможет детям освоить концепцию решения различных математических задач.
Мы также решили несколько задач, которые помогли нам понять концепцию эквивалента. Надеюсь, это поможет детям освоить концепцию решения различных математических задач.
Преподавание математических понятий может быть сложной задачей, особенно для маленьких детей. Итак, чтобы облегчить жизнь родителей и учителей, SplashLearn предлагает несколько курсов, специально разработанных для учащихся K-8. Ведь учиться должно быть весело!
Часто задаваемые вопросы
Каковы примеры эквивалентных значений?
Примерами эквивалентных значений могут быть такие дроби, как $\frac{1}{2}$ и $\frac{2}{4}$. Они оба упрощены на 0,5 каждый. Примером эквивалентного отношения могут быть 1:5 и 2:10, так как после упрощения они оба будут иметь одинаковое значение, что сделает их эквивалентными.
Эквивалентные дроби и эквивалентные отношения — одно и то же?
Да, эквивалентные дроби одинаковы, поскольку это два разных способа представления одного и того же понятия. Эквивалентные отношения, иногда называемые эквивалентными дробями, представляют собой отношения, которые имеют одинаковую пропорцию друг к другу в простейшей форме.
Эквивалентные отношения, иногда называемые эквивалентными дробями, представляют собой отношения, которые имеют одинаковую пропорцию друг к другу в простейшей форме.
Как найти эквивалентные дроби?
Чтобы найти равные дроби, умножаем числитель и знаменатель на одно и то же число.
Какие есть примеры эквивалентных дробей в реальной жизни?
Например, предположим, что мы готовим рецепт, для которого требуется 1/2 стакана сливочного масла. Но у нас на кухне только 1/4 стакана. Можем ли мы еще сделать рецепт? Да! Потому что 1/2 равно 2/4. Таким образом, мы можем использовать две 1/4 чашки масла вместо одной 1/2 чашки.
Меньше или равно
Меньше или равно Отношение — это одно из неравенств, используемых для представления отношения между двумя неравными числами или другими математическими выражениями. Мы знаем, что символ «меньше» используется, чтобы показать, что одна величина меньше другой величины, а символ «равно» используется, чтобы показать, что две величины равны. Точно так же в математике есть символ меньше или равно, который используется, чтобы показать, что одна величина может быть меньше другой величины или равна другой величине.
Точно так же в математике есть символ меньше или равно, который используется, чтобы показать, что одна величина может быть меньше другой величины или равна другой величине.
| 1. | Что меньше или равно? |
| 2. | Меньше или равно символу в словах |
| 3. | Меньше или равно значению |
| 4. | Меньше или равно в числовой строке |
| 5. | Часто задаваемые вопросы о Меньше или равно |
Что меньше или равно?
«Меньше или равно», как следует из названия, означает, что переменная меньше или равна другому числу, переменной или величине. «Меньше или равно» также может быть выражено как не более, не более, максимум и не более. Обратите внимание на следующий рисунок, чтобы увидеть символ, который показывает знак «меньше чем» со спящей линией под ним.
меньше или равно символу в Word
Давайте разберемся с символом меньше или равно в словах на примере. Джеймс работает в универмаге и получает почасовую оплату. Он может работать максимум 8 часов в день. Вы знаете, что здесь подразумевается под термином «максимум»? Это означает, что Джеймс может работать в магазине меньше или равно 8 часам в день. Представим количество часов, отработанных Джеймсом, как x часов. Таким образом, мы можем математически записать данный пример как x ≤ 8.
Джеймс работает в универмаге и получает почасовую оплату. Он может работать максимум 8 часов в день. Вы знаете, что здесь подразумевается под термином «максимум»? Это означает, что Джеймс может работать в магазине меньше или равно 8 часам в день. Представим количество часов, отработанных Джеймсом, как x часов. Таким образом, мы можем математически записать данный пример как x ≤ 8.
Меньше или равно значению
Мы сталкиваемся с некоторыми утверждениями, содержащими знаки ‘≤’ и ‘≥’, которые называются неравенствами. Оба неравенства имеют разный смысл. Мы можем легко понять их в сравнении. Вот некоторые сравнения этих символов и их примеры вместе с их значениями.
| Символ | Пример | Значение |
|---|---|---|
Меньше или равно, ≤ | х ≤ 7 | Значение x меньше или равно 7. |
− 5 ≤ х ≤ 3 | Значение x должно находиться в диапазоне от − 5 до 3, включая оба значения. | |
| Больше или равно, ≥ | х ≥ 2 | Значение x больше или равно 2. |
2 ≥ х ≥ — 1 | Значение x должно находиться в диапазоне от − 1 до 2, включая оба значения. |
Меньше или равно в числовой строке
Неравенства типа меньше или равно и больше или равно представляются по-разному на числовой прямой. Чтобы обозначить их, мы используем замкнутый круг, чтобы отметить предельное значение и указать стрелку на данное условие неравенства. Давайте посмотрим на это на числовой строке, приведенной ниже:
Мы можем видеть, что, когда мы хотим обозначить «x меньше или равно — 5», мы отметили кружком значение — 5 и указали стрелкой на значения меньше — 5, как было предложено в условии неравенства . Точно так же, когда мы хотим обозначить «x больше или равно — 2», мы помечаем кружком значение — 2 и указываем стрелку на значения больше — 2, как это предлагается в условии неравенства.
Связанные темы:
Ознакомьтесь с интересными темами, чтобы узнать больше о меньшем или равном и связанных с ним темах.
- Номер строки
- Больше, чем калькулятор
- Как поставить знак больше или равно
- Больше или равно
Важные примечания:
Ниже приведены примечания, помогающие понять концепцию меньше или равно.
- Одни и те же числа можно складывать или вычитать с обеих сторон неравенства без изменения знака неравенства.
- Одни и те же положительные числа можно либо умножать, либо делить на обе части неравенства без изменения знака неравенства.
- Одни и те же отрицательные числа можно либо умножить, либо разделить в обеих частях неравенства, и знак неравенства изменится на противоположный.
Меньше или равно Примеры
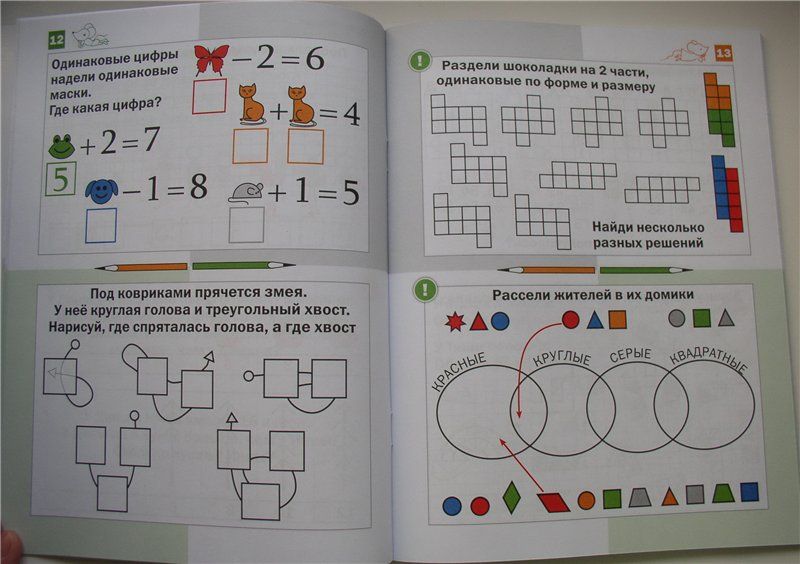
Пример 1: В классе может быть максимум 60 учебных столов.
 Выразите это утверждение с помощью символа меньше или равно.
Выразите это утверждение с помощью символа меньше или равно.Решение:
Представим количество учебных столов переменной x.
Учитывается, что класс может занимать максимум 60 учебных столов.
Итак, это можно представить простым неравенством.
∴ x ≤ 60
Следовательно, условие представляется как x ≤ 60, где x — количество таблиц.
Пример 2: У Чарльза было 18 шоколадных конфет, которые он собирался раздать своим друзьям на свой день рождения. Так как коробка была открыта, по дороге он потерял несколько конфет. Если x — это количество шоколадок, которые есть у Чарльза на данный момент, запишите неравенство, используя символ «меньше или равно», который представляет эту ситуацию.
Решение:
Первоначальное количество шоколадных конфет у Чарльза = 18
Поскольку он потерял несколько шоколадных конфет, количество шоколадных конфет с ним на данный момент меньше 18.

x < 18 ⋯(1)
Мы знаем, что количество конфет должно быть неотрицательной величиной. Следовательно,
x ≥ 0
Это неравенство можно также записать в виде:
0 ≤ x ⋯(2)
Из неравенств (1) и (2) получаем
0 ≤ х < 18Таким образом, количество конфет, которые есть у Чарльза, представлено как 0 ≤ x < 18.
Пример 3: Учительница Джолли попросила ее найти числа, принадлежащие набору, как показано на доске.
Вы можете ей помочь?
Решение:
Мы знаем, что Z — это множество целых чисел.
Дан набор:
{x∈Z|x≤4}
Это означает, что мы должны найти все целые числа, которые меньше или равны 4.
Поскольку набор целых чисел бесконечен, числа, принадлежащие данному набору, следующие:
…, −3, −2, −1, 0, 1, 2, 3, 4
Следовательно, числа в данном наборе есть …, −3, −2, −1, 0, 1, 2, 3, 4.
перейти к слайдуперейти к слайдуперейти к слайду
Разбейте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Меньше или равно
Как вводить меньше или равно?
Меньше или равно представлено символом ≤. Поэтому, если мы хотим записать x меньше или равно 6, мы записываем это как x ≤ 6, что означает, что x может принимать любое значение от отрицательной бесконечности до 6, но не более 6.
Что означает меньше или равно Значить?
Меньше или равно в математике означает, что вы не можете иметь больше, чем что-то, вы должны иметь либо меньше, либо равно заданному пределу. «Меньше или равно», как следует из названия, означает, что число либо меньше, либо равно другому числу. Его также можно выразить как не более, не более, максимум и не превышая.
Как использовать меньше или равно?
Меньше или равно используется для выражения неравенства, когда переменная или выражение может быть меньше или равно числу, переменной или выражению. Например, a ≤ 2, x + y ≤ 6, p ≤ 6q+8 и т. д.
Например, a ≤ 2, x + y ≤ 6, p ≤ 6q+8 и т. д.
В чем разница между Меньше чем и Меньше или равно?
Неравенство «меньше чем» представлено символом <, тогда как неравенство «меньше или равно» представлено как ≤. Неравенство «меньше» означает, что некоторая переменная или число может иметь любое значение, которое меньше заданного предела, не больше или равно этому пределу, а неравенство «меньше или равно» утверждает, что число или переменная может быть равно или меньше заданного предела. Здесь включение лимита является разницей.
Какой пример меньше или равно?
Если у нас есть неравенство: x ≤ 4, это означает, что мы должны найти все целые числа, которые меньше или равны 4. Поскольку множество целых чисел бесконечно, числа, которые принадлежат данному множеству: . ..,−3,−2,−1,0,1,2,3,4.
Какое другое слово означает меньше или равно?
«Меньше или равно» в математике означает, что что-то либо меньше, либо равно другой величине. «Меньше или равно» также может быть выражено как не более, не более, максимум и не более.

 Она была широкая или узкая? Длинная или короткая? Эти понятия мы и будем уточнять на уроке.
Она была широкая или узкая? Длинная или короткая? Эти понятия мы и будем уточнять на уроке. Какой он по счёту?
Какой он по счёту? Повторение состава числа
Повторение состава числа
 Мне надо выбрать длинную ленту, а как это сделать?
Мне надо выбрать длинную ленту, а как это сделать? (5минут)
(5минут)


 Как сравнивали длину ремней?
Как сравнивали длину ремней? Обобщение изученного на уроке и введение его в систему ранее усвоенных знаний.
Обобщение изученного на уроке и введение его в систему ранее усвоенных знаний.
 Выразите это утверждение с помощью символа меньше или равно.
Выразите это утверждение с помощью символа меньше или равно.