ГлавнаяРазноеНеравенства с двумя переменными 9 класс презентация

Презентация к уроку алгебры в 9 классе по теме "Решение систем неравенств с двумя переменными" 1-ый урок. Неравенства с двумя переменными 9 класс презентация


Уравнения и неравенства с двумя переменными Презентации по алгебре 9 класс –

Презентация Решение неравенств с двумя переменными и их систем

Презентация Уравнения с двумя переменными и его график

Презентация Решение систем уравнений второй степени

Презентация Решение неравенств с двумя переменными

Еще больше презентаций

Математический язык — презентация для 5 клас... Геометрические фигуры Презентации по математике 5 ... Презентация Площадь прямоугольного треугольника... Квадратичная функция Презентации по алгебре 9 клас... Квадратичная функция. Функция y = k/x Презентации ... Презентация Координатный луч (математика 5 класс)...

shkolnye-prezentacii.ru

Презентация к уроку алгебры в 9 классе по теме "Решение систем неравенств с двумя переменными" 1-ый урок

Инфоурок › Математика › Презентации › Презентация к уроку алгебры в 9 классе по теме "Решение систем неравенств с двумя переменными" 1-ый урок

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Решение систем неравенств с двумя переменными Кульбянок Ольга Юрьевна. МКОУ «Больше-Желтоуховская СОШ»

2 слайд Описание слайда:

Что значит решить неравенство? Задание "решить неравенство" означает, что требуется найти множество всех его решений. Это множество может оказаться пустым — в случае, когда решений нет. Множество всех решений неравенства будем называть его ответом Как называется запись нескольких неравенств под знаком фигурной скобки? Система неравенств. Что является решением системы неравенств»? Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.

3 слайд Описание слайда:

Является ли пара чисел (1; 2) решением этих систем

4 слайд Описание слайда:

Понятие решения системы с двумя переменными Пара чисел (а;в) значений переменных х и у которая является решением как первого так и второго неравенства системы называется решением системы неравенств с двумя переменными. Что называется множеством решений системы неравенств с двумя переменными?

5 слайд Описание слайда:

Изобразите на координатной плоскости множество решений системы неравенств:

6 слайд Описание слайда:

Упражнения: 1. № 496. 2. № 497 (а, в). 4. № 499 (а).

7 слайд
Описание слайда:

Домашнее задание № 497 (б, г), № 498, № 499 (б).

8 слайд Описание слайда:

Итоги урока Что называется решением системы неравенств с двумя переменными? – Как решаются системы линейных неравенств с двумя переменными

Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДВ-359794

Похожие материалы

Оставьте свой комментарий

infourok.ru

Конспект урока + презентация по алгебре для 9 класса «Неравенства с двумя переменными»

Автор презентации: Руденко Надежда Петровна

Данный урок проводился в рамках месячника открытых уроков. Рассчитан на среднего уровня класс, разработан по учебнику Макарычева Ю.Н. и др. - М. : Просвещение, 2010, пункт 21, относится к уроку изучения нового материала с последующим закреплением изученного. По ходу урока имеется презентация, смена слайдов подробно описана в конспекте, алгоритм выполнения графического решения неравенств с двумя переменными выдавался учащимся на уроке в заранее распечатанном виде и приклеивался в рабочие тетради с целью экономии времени. Конспект пригодится для оказания помощи молодым специалистам, работающим в сельских школах.

"Муниципальное общеобразовательное учреждение«Румянцевская средняя общеобразовательная школа»Истринского муниципального района

Открытый урок по алгебре для учащихся 9 «а» класса (в рамках месячника открытых уроков)

Составила: учитель математики Руденко Н.П. 29.01.2013 года

Ход урока

  1. Повторение изученного материала.По таблицам повторить тему «Элементарные функции и их графики».Работа по карточкам – трое учеников :Карточка 1. Построить график функции:Карточка 2. Построить график функции:Карточка 3. Построить график функции:Остальные учащиеся заполняют вынесенную на доску таблицу: (название линии через некоторый промежуток времени выносится учащимися на доску)
  2. Изучение нового материала:Слайд 1.Выполните устно следующее упражнение:Учащиеся находят отличия в записанных неравенствах (в 2-х неравенствах- по 1 переменной, в остальных – по две)Слайд 2.Определение неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).Рассмотрим неравенство  2х2 – у < 6. При х = 2, у = 5 это неравенство обращается в верное числовое неравенство 2•22 - 5 < 6. Говорят, что пара (2; 5) является решением этого неравенства.Слайд 3.Определение решения неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).Рассмотрим на примерах, как изображается на координатной плоскости мно¬жество решений неравенства с двумя переменными.Слайды 4 - 7. Задание 1. Изучить алгоритм нахождения множества решений неравенства (объяснение учителем по слайдам)(Алгоритм (есть запись на слайде 9), заготовленный заранее учителем, приклеивается в тетрадях учащимися). Так получается быстрее!!!Повторение алгоритма учащимися.
  3. Закрепление изученного материала Слайды 8 – 11. (Открыть только 8 слайд, когда учащиеся перепишут задание, открыть алгоритм выполнения задания на 9 слайде)Задание 2. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству(К доске вызывается 1 ученик)Проверка – на 10,11 слайдах.
  4. Заключительная часть урокаФронтальный опрос учащихся- Что называется решением неравенства с двумя переменными?- Как найти множество решений неравенства с двумя переменными? (повторить 4 пункта алгоритма, если хватает времени, то поспрашивать учащихся)- Всегда ли решением будет полуплоскость? (нет) Доказательство посмотреть на слайдах.Слайды12-14. Решение неравенства (Ответом является часть плоскости – круг)

Итог урока: Выставление оценокЗадание на дом:п.21, выучить правила, №482, №484

Обязательно поделитесь с друзьями: Скачать Размер презентации: 1.13 Mb

edudocs.info

Урок алгебры по теме "Системы неравенств с двумя переменными". 9-й класс

Разделы: Математика

Любому учителю известно, что уроки, посвященные изучению графиков функций, требуют построения большого количества графиков. Чем больше будет построено графиков, тем лучше учащиеся освоят данный материал. Но возникает проблема – ограниченное время урока. Перед учителем встает вопрос о выборе средств и методов обучения с целью обеспечения максимальной эффективности изучения математики. В этом случае приходят на помощь компьютерные технологии. В настоящее время существует много программ, с помощью которых можно рисовать графики функций. Они дают возможность проиллюстрировать свойства функций быстро и наглядно, что повышает и активизирует познавательную деятельность учащихся. На представленном уроке используется программа Advanced Grapher.

Класс: 9.

Технологии: Информационно-коммуникативные технологии.

Оборудование: Компьютер; проектор, интерактивная доска; программа «Advanced Grapher», классная доска; учебник «Алгебра 9 класс». (Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Москва «Просвещение», 2011г.), рабочая тетрадь, карточки-тесты.

Цели:

  • Образовательные – ввести понятие решения системы неравенств с двумя переменными; формировать умение решать системы неравенств с двумя переменными, отработать навыки построения множества решений систем неравенств на координатной плоскости;
  • Развивающие – формирование графической и функциональной культуры учащихся;
  • Воспитательные – воспитание интереса к математике и повышение мотивации учебной деятельности через внедрение компьютерных технологий в процесс обучения, побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.

Ход урока

Актуализация знаний.

Учитель. На доске вы видите два неравенства

х2+3ху –у2<20 и (х-3)2+(у-4)2<2

  • Как они называются? [Неравенства с двумя переменными]
  • Что является решением такого неравенства? [Пара чисел, которые удовлетворяют неравенству]
  • Определите, является ли пара чисел (-2;3) решением какого либо из этих неравенств? [Являются решением только первого неравенства]
  • Найдите свою пару чисел которая являлась бы решением второго неравенства [Например 3 и 4, 4 и 4, 3 и 5 и т.д.]

Проверка домашнего задания.

Учитель Давайте вспомним , как решаются такие неравенства.

На примере неравенств х2+2 > у и (x-1)^2+(y+2)^2<4 рассказать о решении неравенств с двумя переменными.

Двое учащихся рассказывают и показывают решение неравенств на доске.

  • Чем отличается решение строгого неравенства от нестрогого? [линия функии штриховая]
  • Как можно проверить правильно ли вы выбрали множество? [Правило пробной точки]

Проверим решение №484б и г с помощью программы «Advanced Grapher» на интерактивной доске. (Учитель открывает готовый файл Приложение 1.agr. В окне слева выбирает первую и вторую функцию

Чтобы проверить решение второго неравенства отмените построение предыдущих двух и выберите следующие две)

[Учащиеся сравнивают решение в тетрадях с изображением на интерактивной доске.]

Тестовая работа.

на готовых карточках- координатных плоскостях (Приложение 2) показать решения неравенств а) х>2, б) у<-2; в) -3<у<3; г)│х│<у ; д)│ х-2│>у с последующей проверкой на интерактивной доске с помощью программы «Advanced Grapher». (Приложение 1. agr)

Новая тема.

Учитель. Тема сегодняшнего урока «Системы неравенств с двумя переменными»

  • Как вы думаете, каковы цели сегодняшнего урока?
  • Чему вы должны научиться к концу сегодняшнего урока?

Рассмотрим систему неравенств с двумя переменными.

№496

  • Как вы думаете, что же может, является решением такой системы? [Пара чисел]
  • Какие из пар (4;2), (-5;1), (-2;-1) являются решением этой системы? [Первая]
  • Как по-вашему, сколько решений может иметь такая система? [Множество]
  • Что значит решить систему?c[Найти все решения, или доказать, что таких решений нет]

Учитель. Давайте выясним, какое множество точек задает на координатной плоскости система. Как это сделать? [Решить по отдельности каждое неравенство и найти их пересечение решений.]

Пример 1

Ребята в тетрадях рисуют графики функций, а учитель поэтапно показывает графики на интерактивной доске (Приложение 1.agr)

Как можно проверить правильно ли показано множество решений? [Правило пробной точки]

Пример 2. Выполнение в тетради, затем поэтапная проверка на интерактивной доске (Приложение 1.agr)

Пример 3 Выполнение в тетради, затем поэтапная проверка на интерактивной доске (Приложение 1.agr)

Закрепление.

№497 а, в на обычной доске [Одновременное решение на доске и в тетрадях]

Итоги урока.

– Что называется решением системы неравенств с двумя переменными?

– Как решаются системы линейных неравенств с двумя переменными?

– Как проверить верно ли выбрано решение?

Домашнее задание.

№ 497 (б, г), Доп.задание: Изобразите на координатной плоскости множество решений системы неравенств:

Приложение.

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Элективный курс по математике для 9 класса «Неравенства и системы неравенств с двумя переменными»

Слайды и текст этой презентации

Слайд 1

Министерство Образования РХ МОУ «Копьевская средняя общеобразовательная школа»Элективный курс по математике для предпрофильной подготовки учащихся 9 класса Автор: Зубкова Л. И., учитель математики . Неравенства и системы неравенств с двумя переменными

Слайд 2

Пояснительная запискаЭлективный курс для учащихся 9 класса «Неравенства и системы неравенств с двумя переменными» углубляет ранее приобретенные знания при построении графиков различных функций и расширяет представления учащихся о взаимосвязи между алгебраическими соотношениями и их геометрическими образами на координатной плоскости.

Слайд 3

Задачи курса:-создание ситуации успеха для каждого обучающегося с учетом уровня его развития; -формирование умений использовать приемы логических рассуждений при решении задач; -совершенствование представлений о специфике учебной деятельности в классах математического профиля; -развитие умений группового общения.

Слайд 4

Задачи содержанияСодержание курса позволяет ученику любого уровня активно включаться в учебно –познавательный процесс и максимально проявить себя, группируется в соответствии с индивидуальными различиями учащихся в обученности, общих и математических умственных способностях, направленности познавательных интересов.

Слайд 5

Методика курсаМетодика изучения данного курса ориентирована, прежде всего, на овладение практическими навыками на основе минимального объема теории. Большая часть-уроки-практикумы, на которых проводится коллективное обсуждение решений с помощью учителя, работа в группах. Выделяется время на самостоятельную работу учащихся в классе и дома с целью проверки результативности работы. С некоторыми заданиями удобнее работать индивидуально, с последующим обсуждением результатов.

Слайд 6

Требования к учащимсяЗнать и уметь применять: 1)-понятие неравенства; 2)-понятие системы неравенств; 3)-определение функций и их графики; 4)-способы преобразования графиков .

Слайд 7

Требования к учащимся :Уметь: 1) строить графики функций; 2) изображать на плоскости решение неравенств и систем неравенств.

Слайд 8

Тема 1Линейная функция. Обратная пропорциональность. Свойства и графики.

Слайд 9

Тема 2Квадратичная функция. Свойства и график. Уравнение окружности. Уравнение эллипса. Их графики. Преобразование графиков.

Слайд 10

Тема 3Задание областей координатной плоскости линейными неравенствами с двумя переменными и системой таких неравенств. Геометрическая интерпретация нелинейных неравенств с двумя переменными и их систем.

Слайд 11

Тема 4 Решение текстовых задач с помощью систем неравенств.

Слайд 12

Рекомендуемая литература1.Алгебра.8кл.:Учебник для класса с углубленным изучением математики/ Ю.Н.Макарычев, Н. Г. Миндюк, К. И.Нешков,-6 изд., Мнемозина, 2006,-367с 2. 1.Алгебра.9кл.:Учебник для класса с углубленным изучением математики/ Ю.Н.Макарычев, Н. Г. Миндюк, К. И.Нешков,-4 изд., Мнемозина, 2005,-439с 3.Г. В. Дородиев и др.Курс по выбору для 9класса «Избранные вопросы математики».Математика в школе.-2003г. N10,стр. 19. 4.Н.В.Коржуев, Н.Э. Богатырева. Обучение решению текстовых задач с неравенствами. Математика в школе.-1993г.N3,стр.54.

Слайд 13

Текстовые задачи (приложение 1)1. Прибывших на парад солдат планировали построить так, чтобы в каждом ряду стояло по 24 человека. Но в действительности не все прибывшие смогли участвовать в параде, и их перестроили так., что число рядов стало на 2 меньше, а число человек в ряду на 26 больше нового числа рядов. Если бы все солдаты участвовали в параде, то их можно было бы построить так, чтобы число рядов было равно числу человек в ряду. Сколько солдат прибыло на парад? 2. Из двух целых положительных чисел второе больше квадрата первого. Сумма квадрата разности первого числа и 3 и квадрата разности второго и 4 меньше 4. Найти эти числа.

Слайд 14

Преобразование графиков(инверсия) (приложение 2)Определение: Две точки А и В называются инвертными относительно некоторой прямой l (оси), если выполнены три условия:1)Точки А и В лежат по одну сторону от прямой l 2)Прямая АВ перпендикулярна l 3)Произведение расстояний от точки А до оси l и точки В до оси l равно единице. Для точек на оси инверсия не определена

Слайд 15

Преобразование графиков (приложение 2)Определение : Отображение плоскости на себя при котором каждая ее точка переходит в инвертную ей относительно данной прямой называется инверсией плоскости (для точек оси понятие инверсии не определено ) Теорема : График функции g(x)=1/f(x)получается из графика функции y=f(x) с помощью инверсии относительно оси х.

Слайд 16

Приложение 2

Слайд 17

Формы контроля уровня достижений уч-ся и критерии оценок (приложение 3)При промежуточном контроле выставляется оценка «5» или «4». Итоговая оценка будет выставляться в форме «зачтено/не зачтено»

Слайд 18

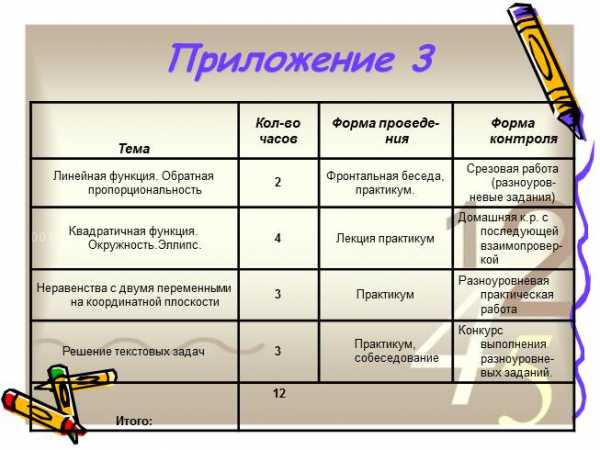
Приложение 3Тема Кол-во часов Форма проведе-ния Форма контроля Линейная функция. Обратная пропорциональность 2 Фронтальная беседа, практикум. Срезовая работа (разноуров- невые задания) Квадратичная функция. Окружность.Эллипс. 4 Лекция практикум Домашняя к.р. с последующей взаимопровер-кой Неравенства с двумя переменными на координатной плоскости 3 Практикум Разноуровневая практическая работа Решение текстовых задач 3 Практикум, собеседование Конкурс выполнения разноуровне-вых заданий. Итого: 12     12     12    

lusana.ru

Презентация решение систем неравенств 9 класс

(9 класс)

А. Нивен

Запомним

Решить систему неравенств – это значит найти значение переменной , при котором верно каждое из неравенств системы.

Запомним

Если надо решить систему неравенств, то :

  • решаем каждое неравенство системы отдельно
  • изображаем полученные решения на числовой прямой и смотрим пересечения этих решений.

Эта общая часть и является решением данной системы неравенств.

Содержание

  • Решение систем линейных неравенств
  • Решение двойных неравенств
  • Решение систем, содержащих квадратные неравенства
6 2х – 4 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 5х 6 -1 2х 5х 5 2х х 1 х 1 3,5 х Ответ: (1; 3,5)"

Решим систему неравенств (состоящую из линейных неравенств)

5х + 1 6

2х – 4

Решение: решим каждое неравенство отдельно

5х + 1 6 2х – 4

5х 6 -1 2х

5х 5 2х

х 1 х

1 3,5 х

Ответ: (1; 3,5)

- 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4]"

Решим систему неравенств

5х + 12 ≤ 3х+ 20

х

2х + 7 ≥ 0

Решение: решим каждое неравенство отдельно

5х + 12 ≤ 3х+ 20 х 2х + 7 ≥ 0

5х – 3х ≤ - 12 + 20 х – 2х

2х ≤ 8 -х

х ≤ 4 х - 3 х ≥ -3,5

Изобразим на числовой прямой:

-3,5 -3 4

Ответ: ( -3; 4]

12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [2; +∞) 2) Нет решения"

Работа в парах:

Решить систему

неравенств:

1) 3х – 2 ≥ х + 1

4 – 2х ≤ х – 2

2) 3х 12 + 11х

5х – 1 ≥ 0

Проверим ответы:

1) [2; +∞)

2) Нет решения

Примеры двойных неравенств

Прочитайте неравенства :

-6 х 0

-1,2 ≤ х 3,5

0 х ≤ 5,9

0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 0 2) 4х + 2 ≤ 6 х - 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 или (-0,5; 1]"

Решение двойных неравенств

Решить неравенство: 0 4х +2 ≤ 6

Решение: составим систему: 4х + 2 0

4х + 2 ≤ 6

Решим каждое неравенство системы отдельно:

1) 4х + 2 0 2) 4х + 2 ≤ 6

х - 0,5 х ≤ 1

Полученные результаты изобразим на числовой прямой:

-0,5 1 х

Ответ: -0,5 или (-0,5; 1]

Решите неравенства, работая в парах

Решить неравенства:

Проверим

ответы:

1) [-1; 2]

2) (2,5; 7 ]

3) [- 1,5; - 1)

4) (-2; 1)

5) (-4; 0)

  • -6 ≤ - 3х ≤ 3
  • 4 ≤ 13
  • -2 ≤ 6х + 7 1
  • 0,3
9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; +∞)"

Решим систему неравенств (в которую входит квадратное неравенство)

Решить систему неравенств: х ² - 5х + 4 ≤ 0

9 - 4х

Решение: решим каждое неравенство системы отдельно

1) х ² - 5х + 4 ≤ 0 2) 9 - 4х

х ² - 5х + 4 = 0 - 4х

т.к. а+в+с=0, то х 1 =1; х 2 =4 х 9/4=2,25

Полученные результаты изобразим на числовой прямой:

1 2,25 4 х

Ответ: [ 4; +∞)

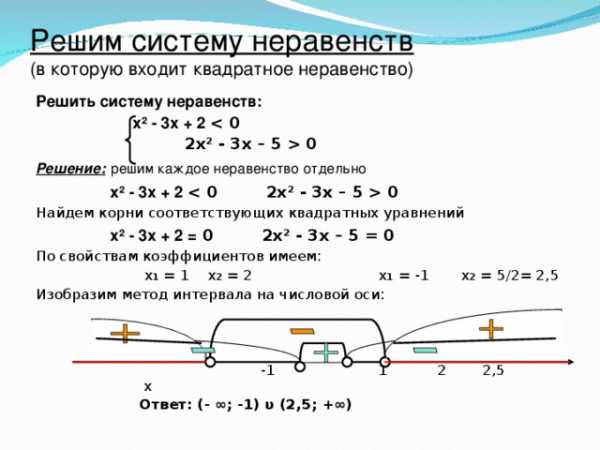0 Решение: решим каждое неравенство отдельно х ² - 3х + 2 2х² - 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² - 3х + 2 = 0 2х² - 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞)"

Решим систему неравенств (в которую входит квадратное неравенство)

Решить систему неравенств:

х ² - 3х + 2

2х² - 3х – 5 0

Решение: решим каждое неравенство отдельно

х ² - 3х + 2 2х² - 3х – 5 0

Найдем корни соответствующих квадратных уравнений

х ² - 3х + 2 = 0 2х² - 3х – 5 = 0

По свойствам коэффициентов имеем:

х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5

Изобразим метод интервала на числовой оси:

-1 1 2 2,5 х

Ответ: (- ∞; -1) υ (2,5; +∞)

0 4х – 1 ≥ 0 2) 4х² - 1 ≤ 0 х² 1 3х² - 2х – 1 х² - х – 6 0"

Решим системы неравенств, работая вместе

1) 6х² - 5х + 1 0

4х – 1 ≥ 0

2) 4х² - 1 ≤ 0

х² 1

х² - х – 6 0

0 4х – 1 ≥ 3 3) 2х² - 7х + 5 2 – х ≥ 0 Проверим ответы: 1) (4; 9 ] 2) [1; 2) 3) (- ∞ ; 1 )"

Решите системы неравенств, работая самостоятельно

1) х² - 10х + 9 ≥ 0

12 – 3х

2) 2х²- 5х + 2 0

4х – 1 ≥ 3

3) 2х² - 7х + 5

2 – х ≥ 0

Проверим ответы:

1) (4; 9 ]

2) [1; 2)

3) (- ∞ ; 1 )

kopilkaurokov.ru

Системы Неравенств С Двумя Переменными 9 Класс Презентация

Системы Неравенств С Двумя Переменными 9 Класс Презентация Rating: 3,7/5 5129votes

Уравнения и неравенства с двумя переменными по предмету алгебра за 1. Тема: Уравнения и неравенства. Системы уравнений и неравенств. Урок: Уравнения и неравенства с двумя переменными. Рассмотрим в общем виде уравнение и неравенство с двумя переменными. Можно перефразировать данную задачу – найти геометрическое место точек (ГМТ), построить график уравнения или неравенства. Пример 1 – решить уравнение и неравенство: Иначе говоря, задача подразумевает найти ГМТ.

Системы Неравенств С Двумя Переменными 9 Класс Презентация Макарычев

Рассмотрим решение уравнения. В данном случае значение переменной х может быть любым, в связи с этим имеем: Очевидно, что решением уравнения является множество точек, образующих прямую Рис. График уравнения, пример 1. Решениями заданного уравнения являются, в частности, точки (- 1; 0), (0; 1), (х. Руководство По Ремонту Иж Юпитер 5 Скачать Бесплатно. Решением заданного неравенства является полуплоскость, расположенная над прямой , включая саму прямую (см. Действительно, если взять любую точку х.

Если же взять точку в полуплоскости над прямой, имеем . Если мы возьмем точку в полуплоскости под прямой, то она не удовлетворит нашему неравенству: . Теперь рассмотрим задачу с окружностью и кругом. Пример 2 – решить уравнение и неравенство: Мы знаем, что заданное уравнение – это уравнение окружности с центром в начале координат и радиусом 1.

Похожие презентации. Системы линейных уравнений с двумя переменными. Решение уравнений, неравенств и их систем с модулями, 9 класс.

Рис. Иллюстрация к примеру 2. В произвольной точке х. Решением заданного неравенства является множество точек, расположенных внутри окружности, не учитывая саму окружность (см. Несложно заметить, что график данного уравнения симметричен относительно обеих осей. Тогда если точка (х. Таким образом, достаточно найти решение там, где обе переменные неотрицательны, и взять симметрию относительно осей: Рис.

Cкачать: Урок Системы неравенств с двумя переменными. Первым рассматривается решение системы неравенств х2+у2<=9 и .

  1. РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ (8 КЛАСС) · Решение систем неравенств с двумя переменными. Презентация на тему: Решение систем неравенств. Скачать эту презентацию. Получить код Наши баннеры. Решение систем неравенств Павлова Лариса ВасильевнаШкола 403.
  2. Презентация 9 класса по предмету "Математика" на тему: "Алгебра 9 класс «Графическое решение неравенств с двумя переменными» урок 2 Учитель: .
  3. Решение систем неравенств с двумя переменными. Кнопки: Презентация на тему: Решение систем неравенств 9 класс .
  4. Презентация была опубликована 3 года назад пользователемИнна. 9 Сколько решений имеет система в зависимости от параметра а? Факультативное занятие в 11 классе: Графический подход к решению задач с .
  5. Ориентирован на учебник: «Алгебра. Содержит 31 видеоурок, 31 презентацию и 31 тест. Системы неравенств с двумя переменными.
  6. Разработка трёх уроков по теме "Системы неравенств с двумя переменными" 9 класс.

Иллюстрация к примеру 3. Итак, как мы видим, решением уравнения является квадрат. Рассмотрим так называемый метод областей на конкретном примере. Пример 4 – изобразить множество решений неравенства: Согласно методу областей, первым делом рассматриваем функцию, стоящую в левой части, если справа ноль. Это функция от двух переменных: Аналогично методу интервалов, временно отходим от неравенства и изучаем особенности и свойства составленной функции. ОДЗ: , значит, ось х выкалывается.

Теперь укажем, что функция равна нулю, когда числитель дроби равен нулю, имеем: Строим график функции. График функции , учитывая ОДЗТеперь рассмотрим области знакопостоянства функции, они образованы прямой  и ломаной . Между отрезком ломаной  и прямой  – область D2, ниже прямой  – область D3, между отрезком ломаной  и прямой  – область D4. В каждой из выбранных областей функция сохраняет знак, значит достаточно в каждой области проверить произвольную пробную точку. В области  возьмем точку (0; 1). Имеем: Так, вся область  положительна и удовлетворяет заданному неравенству. В области  возьмем точку (1.

Имеем: Так, вся область  отрицательна и не удовлетворяет заданному неравенству. В области  возьмем точку (0; -5). Имеем: Так, вся область  положительна и удовлетворяет заданному неравенству. В области  возьмем точку (- 3; 1). Имеем: Так, вся область  отрицательна и не удовлетворяет заданному неравенству.

Изобразим множество решений неравенства, как требовалось в задаче: Рис. Решение примера 4. Итак, мы рассмотрели решение различных уравнений и неравенств с двумя переменными, на следующем уроке одну из переменных назовем параметром. Список литературы. Мордкович А. Г. Алгебра и начала математического анализа. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа.

Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П.

Алгебра и начала математического анализа. Tutoronline. ru (Источник). Tutoronline. ru (Источник). Nado. 5. ru (Источник). Домашнее задание. Фильм Экстра На Немецком подробнее. Решить уравнение: а) ; б) ; в) ; г) ; 2.

Решить неравенство: а)  б) ; в) ; г) .

villedownloadfree.netlify.com