Конспект урока 8 класс измерение информации: План-конспект урока по теме «Единицы измерения информации» (8 класс, учебник Семакина)

Содержание

План-конспект урока по теме «Единицы измерения информации» (8 класс, учебник Семакина)

ПЛАН-КОНСПЕКТ УРОКА

«Измерение информации. Единицы измерения
информации»

8 класс

Учитель
информатики Алена Павловна Куриляк, МБОУ «Полазненская средняя
общеобразовательная школа №3»

Цель урока: познакомить
с понятиями: «измерение информации», «алфавит», «мощность алфавита», «алфавитный
подход в измерении информации», научить измерять информационный объём
сообщений, с учётом информационного веса символов.

Тип урока: объяснительно-демонстрационный
с элементами практикума.

Нагляднось: презентация
«Измерение информации».

Учебная литература: учебник
«Информатика». 8-й класс (базовый курс) И.Г.Семакин, «Информатика»
задачник-практикум (1 часть) И.Г.Семакин.

Требования к знаниям и умениям:

Учащиеся должны знать:

·
что такое «алфавит», «мощность алфавита», «алфавитный
подход в измерении информации»;

·
как измерить информационный объём;

·
как определяется единица измерения
информации бит;

·
что такое байт, килобайт, мегабайт,
гигабайт.

Учащиеся должны уметь:

·
приводить примеры сообщений, несущих 1 бит
информации;

·
измерять информационный объем текста;

·
представлять количество полученной
информации в различных единицах (битах, байтах, килобайтах, мегабайтах,
гигабайтах).

План урока

I. Орг.
момент — 1 мин.

II. Проверка
домашнего задания — 2 мин.

III. Новый
материал. Измерение информации. Алфавитный подход — 25 мин.

IV. Закрепление
изученного — 14 мин.

V. Подведение
итогов урока. — 2 мин.

VI. Домашнее
задание — 1 мин.

Содержание урока

I. Орг. момент.

II. Проверка домашнего задания.

Задачник-практикум
№ 1. с. 11 № 2, 5, 8, 11, 19^*.

III. Новый материал.

1. Введение.

Процесс
познания окружающего мира приводит к накоплению информации в форме знаний.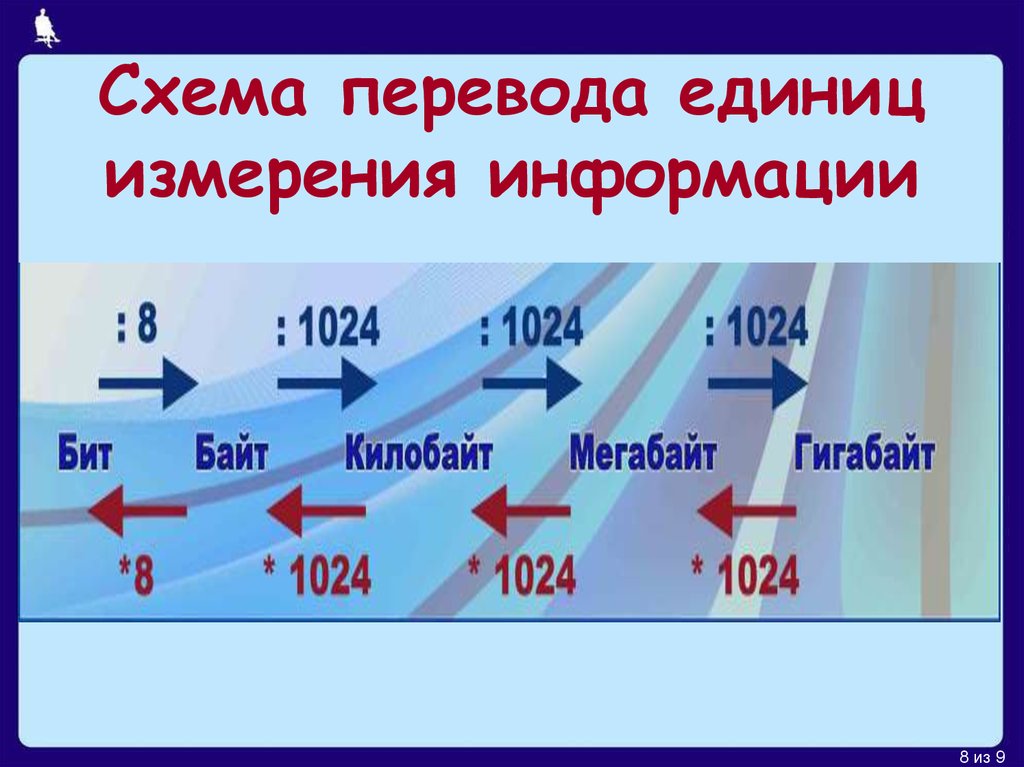

Как
же узнать, много получено информации или нет?

Необходимо
измерить объём информации. А как это сделать мы сегодня узнаем.

Получение
новой информации приводит к расширению знаний или, как иначе можно сказать, к
уменьшению неопределённости знания.

Если
некоторое сообщение приводит к уменьшению неопределённости нашего знания, то
можно сказать, что такое знание содержит информацию.

2. Как можно измерить количество информации.

Для
измерения различных величин существуют эталонные единицы измерения.

Например:

·
Расстояние измеряют в миллиметрах,
сантиметрах, дециметрах…

·
Массу измеряют в граммах, килограммах,
тоннах…

·
Время измеряют в секундах, минутах,
сутках, годах…

Следовательно,
для измерения информации должна быть введена своя эталонная единица.

Существует два подхода к измерению информации:

а) Содержательный (вероятностный). Количество
информации связывается с содержанием (смыслом) полученного сообщения или с
учётом вероятности событий.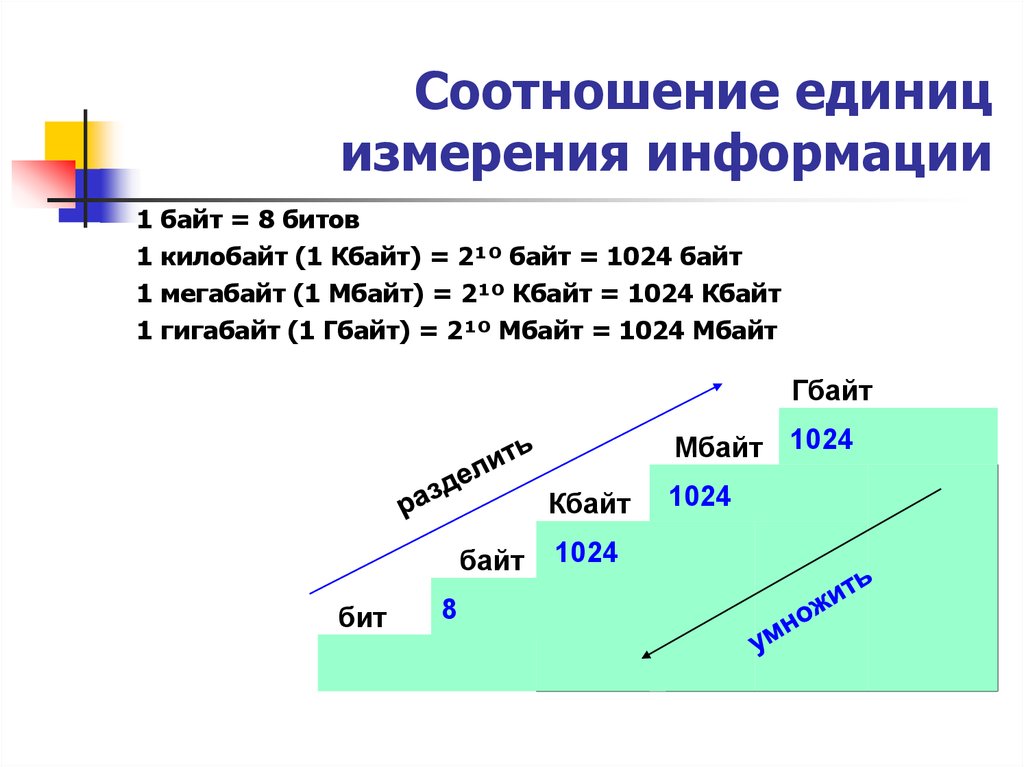

б) Алфавитный. Позволяет
измерять информационный объём текста на любом языке (естественном или
формальном), при использовании данного подхода объём информации не связывают с
содержанием текста, в данном случае, объём зависит от информационного веса
символов.

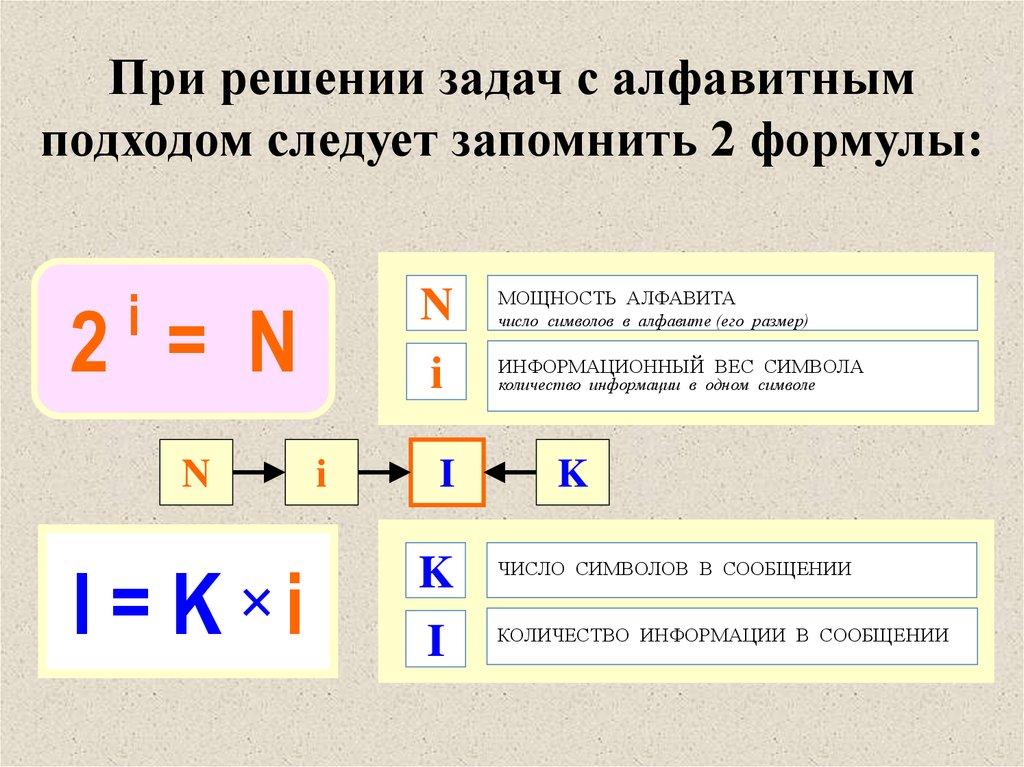
3. Алфавитный подход к измерению информации.

—
Давайте вспомним, что же такое алфавит?

·
Алфавит – весь набор букв, знаков
препинания, цифр, скобок и других символов, используемых в тексте.

*Алфавит
включают и пробел (пропуск между словами).

—
Что такое мощность алфавита?

·
Мощность алфавита — полное число символов
в алфавите.

Например:
мощность алфавита русских букв и используемых символов равна 54:

33
буквы + 10 цифр + 11 знаков препинания, скобки, пробел.

Наименьшую
мощность имеет алфавит, используемый в компьютере (машинный язык), его называют
двоичным алфавитом, т.к. он содержит только два знака «0», «1».

Информационный
вес символа двоичного алфавита принят за единицу измерения информации и
называется 1 бит.

Попробуйте определить объём информационного сообщения:

Информация,
записанная на машинном языке, весит:

01110
— … бит

010010
— … бит

010
— … бита

0111111011110
— … бит

При
алфавитном подходе считают, что каждый символ текста, имеет информационный вес.

Информационный
вес символа зависит от мощности алфавита.

С
увеличением мощности алфавита, увеличивается информационный вес каждого
символа.

Для
измерения объёма информации необходимо определить сколько раз информация равная
1 биту содержится в определяемом объёме информации.

Например:

1)
Возьмём четырёхзначный алфавит (придуманный)

Все
символы исходного алфавита можно закодировать всеми возможными комбинациями,
используя цифры двоичного алфавита.

Получим
двоичный код каждого символа алфавита. Для того чтобы закодировать символы
алфавита мощность которого равна четырём, нам понадобится два символа двоичного
кода.

Следовательно, каждый символ четырёхзначного алфавита
весит 2 бита.

2)
Закодируйте с помощью двоичного кода каждый символ алфавита, мощность которого
равна 8.

Вывод.
Весь алфавит, мощность которого равна 8 можно закодировать на машинном языке с
помощью трёх символов двоичного алфавита.

—
Как вы думаете, каков информационный объём каждого символа восьмизначного алфавита?

Каждый символ восьмизначного алфавита весит 3 бита.

3).
Закодируйте с помощью двоичного кода каждый символ алфавита, мощность которого
равна 16.

—
Какой можно сделать вывод?

Алфавит
из шестнадцати символов можно закодировать с помощью четырёхзначного двоичного
кода.

—
Решите задачу.

Задача: Какой объём
информации содержат 3 символа 16 – символьного алфавита?

Решение:

Так
как каждый символ алфавита мощностью 16 знаков можно закодировать с помощью
четырёхзначного двоичного кода, каждый символ исходного алфавита весит 4 бита.

Так
как всего использовали 3 символа алфавита мощностью 16 символов, следовательно:
4 бит • 3 = 12 бит

Ответ:
объём информации записанный 3 знаками алфавита мощностью 16 символов равен 12
бит.

Запишем
таблицу соответствия мощности алфавита (N) и количеством знаков в коде (b) —
разрядностью двоичного кода.

Вывод.

Информационный
вес каждого символа, выраженный в битах (b), и мощность алфавита (N) связаны
между собой формулой: N = 2^b

Алфавит,
из которого составляется на компьютере текст (документ) состоит из 256
символов.

Этот
алфавит содержит символы: строчные и прописные латинские и русские буквы,
цифры, знаки арифметических операций, всевозможные скобки, знаки препинания и
другие символы.

—
Узнайте, какой объём информации содержится в одном символе алфавита, мощность
которого равна 256.

Решение.
Из формулы N = 2^b следует 256 = 2⁸.

Вывод.
Значит, каждый символ алфавита используемого в компьютере для печати документов
весит 8 бит.

Эту
величину приняли так же за единицу измерения информации и дали название байт.

8 бит = 1 байт

Задача. Статья содержит 30
страниц, на каждой странице — 40 строк, в каждой строке 50 символов. Какой
объём информации содержит статья?

Ход решения.

1)
На каждой странице 50 • 40 = 2000 символов;

2)
во всей статье 2000 • 30 = 60000 символов;

3)
т.к. вес каждого символа равен 1 байту, следовательно, информационный объём
всей статьи 60000 • 1 = 60000 байт или 60000 • 8 = 480000 бит.

— Как видно из задачи байт «мелкая»
единица измерения информационного объёма текста, поэтому для измерения больших
объёмов информации используются более крупные единицы.

Единицы измерения информационного объёма:

1
килобайт = 1 Кб = 210 байт = 1024 байт

1
мегабайт = 1 Мб = 210 Кб = 1024 Кб

1
гигабайт = 1 Гб = 210 Мб = 1024 Мб

—
Попробуйте перевести результат задачи, в более крупные единицы измерения:

60000
байт • 58,59375 Кб

60000
байт • 0,057 Мб

IV. Закрепление изученного.

Задачник-практикум
№ 1. С. 19 № 19, 20, 22, 23, 25.

V. Подведение итогов.

VI. Домашнее задание.

Задачник-практикум
№ 1.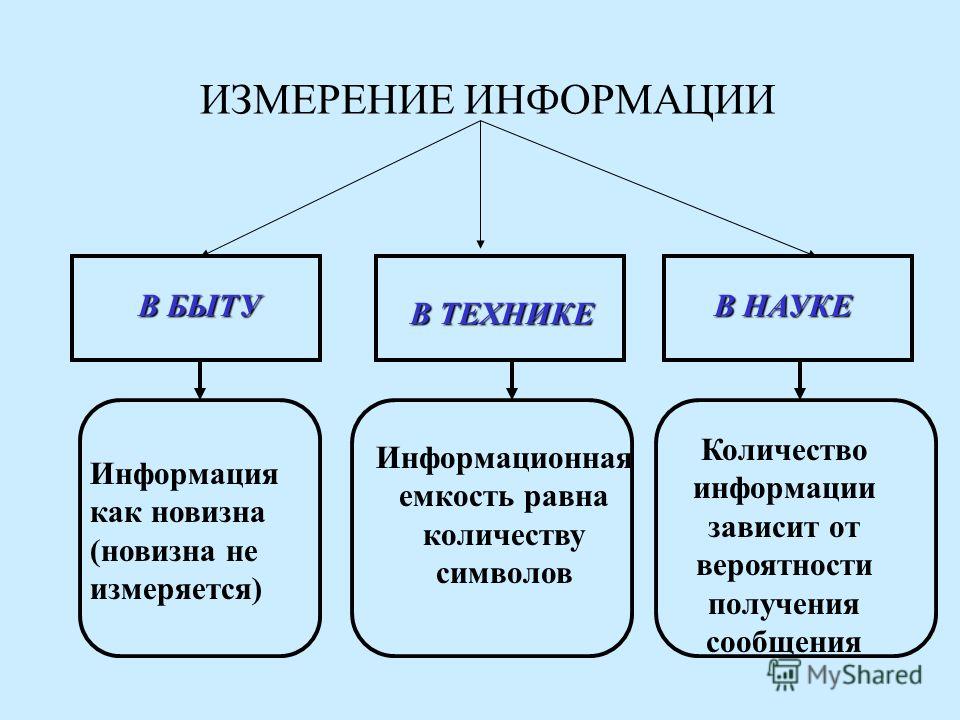 с. 20 № 21, 24, 26.

Урок информатики в 8-ом классе (№1) Тема: «Измерение информации. Содержательный и алфавитный подход к измерению информации» | План-конспект урока по информатике и икт (8 класс) на тему:

Урок информатики в 8-ом классе (№1)

Тема: «Измерение информации. Содержательный и алфавитный подход к измерению информации»

Цель: Обобщающий урок по теме, самостоятельная работа.

Задачи:

образовательные – дать понятие количества информации, познакомить с содержательным и алфавитным подходом при определении количества информации, познакомить с единицами измерения информации, формировать практические навыки по определению количества информации.

развивающие – продолжить формирование научного мировоззрения, расширять словарный запас по теме «Информация».

воспитательные – формировать интерес к предмету, воспитывать настойчивость в преодолении трудностей в учебной работе.

Метод обучения: объяснительно-иллюстративный.

Тип урока: комбинированный.

Формы учебной работы учащихся:

фронтальная работа, работа в группах, индивидуальная работа.

Основные понятия: алфавит, мощность алфавита, информационный вес символа в алфавите, производные единицы измерения информации.

Оборудование:

доска,
маркер,
мультимедийная установка,
компьютеры,
стенды с тематической информацией,
Программное обеспечение: Mytest, PowerPoint,

План урока:

1.Орг.момент.

2.Повторение пройденного материала в 7 классе.

3. Активация познавательной деятельности

4.Физкультминутка.

5.Закрепление материала. Решение задач.

6.Подведение итогов.

Домашнее задание.

Ход урока:

1. Организационный этап (приветствие, определение отсутствующих на уроке, готовность учащихся к уроку) (1 мин.)

2. Повторение пройденного материала в 7 классе. (см. мультимедийную презентацию)

1. Сегодня мы с вами вспомним, что такое информация, как она изменяется,в каких единицах измеряется .

Мы с вами говорили о том, что в основе нашего мира лежат три составляющие – вещество, энергия и информация.

— Можно ли измерить вещество? (можно взвесить, определить длину, найти объем и т.д.)

— Можно ли определить количество энергии? (можно тепловую, электроэнергию и т.д.)

— Но как измерить количество информации?

Количество информации в одном том же сообщении, с точки зрения разных людей, может быть разным. Пример, для человека, не владеющего китайским языком, вывеска на китайском языке не несёт никакой информации. Информативным для человека является то сообщение, которое содержит новые и понятные сведения.

Задание № 1. Определите количество информации с позиции «информативно» или «не информативно».

Столица России – Москва (не инф., т.к. уже знаем).
Сумма квадратов катетов равна квадрату гипотенузы (не инф., уже знаем).
Эйфелева башня имеет высоту 300 метров и вес 9000 тонн (инф.).
Дифракцией света называется совокупность явлений, которые обусловлены волновой природой света и наблюдаются при его распространении в среде с резко выраженной оптической неоднородностью (не инф. , т.к. непонятно).

Следует отличать понятия информация и информативность.

— Содержит ли учебник физики 8 класса информацию? (да)

— Для кого он будет информативным – для ученика 8 класса или 1 класса? (для ученика 8 класса)

Вывод: количество информации зависит от информативности.

Информативность можно обозначить 1, не информативная информация равна 0. Но это не даёт точного определения количества информации.

Существует 2 подхода при определении количества информации – содержательный и алфавитный. Содержательный применяется для измерения информации, используемой человеком, а алфавитный – компьютером.

Компьютер не понимает смысла информации, поэтому для её измерения нужен другой подход. Информация передаётся с помощью сигналов. Горит зелёный свет – можно переходить улицу, горит красный – стой. Поднял руку на уроке – учитель понял, что ты можешь ответить на его вопрос. В этих примерах сигнал имеет два состояния, их двух вариантов мы выбираем один.

Сообщение содержит информацию, если оно приводит к уменьшению неопределенности наших знаний.

Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений. (Выделенное курсивом учащиеся записывают в тетрадь).

Для количественного выражения любой величины необходимо определить единицу измерения. Например, для измерения длины выбран определенный эталон метр, массы – килограмм.

Минимальная единица информации называется бит.

1 бит – это такое количество информации, уменьшающее неопределенность знаний в два раза.

Чтобы закодировать все символы нужна комбинация из 8 нулей и единиц, подобный набор называют двоичным кодом и это составляет

1 байт = 8 бит = 1 символ.

1 килобайт=1024 байт

1мегабайт=1024 килобайт

1 гигабайт=1024 мегабайт

1 терабайт=1024 гигабайт

//Для человека получение новой информации приводит к расширению знаний, или к уменьшению неопределенности. Например, сообщение о том, что завтра среда, не приводит к уменьшению неопределенности, поэтому оно не содержит информацию.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. Мы знаем до броска, что может произойти одно из двух событий – монета окажется в одном из двух положений: «орел» или «решка». После броска наступает полная определенность (визуально получаем информацию о том, что выпал, например, «орел»). Информационное сообщение о том, что выпал «орел» уменьшает нашу неопределенность в 2 раза, так как получено одно из двух информационных сообщений.

В окружающей действительности достаточно часто встречаются ситуации, когда может произойти больше, чем 2 равновероятных события. Так, при бросании шестигранного игрального кубика – 6 равновероятных событий. Событие выпадение одной из граней кубика уменьшает неопределенность в 6 раз. Чем больше начальное число событий, тем больше неопределенность нашего знания, тем больше мы получим информации при получении информационного сообщения. //

3. Активация познавательной деятельности

N = 2 I, где N – количество возможных событий, I – количество информации.

Задача № 1. Сколько бит информации несет сообщение о том, что из колоды карт достали даму пик?

Ответ: 32=2 I, т.е. I=5 бит

3. Алфавитный подход к измерению информации (5 мин.)

Суть алфавитного подхода к измерению информации определяется по количеству использованных для ее представления знаков некоторого алфавита. Например, если при представлении числа XVIII использовано 5 знаков римского алфавита, то это и есть количество информации. То же самое число, т. е. ту же самую информацию, можно записать в десятичной системе (18). Как видим, получается 2 знака, т. е. другое значение количества информации.

Алфавит – конечный набор символов, используемых для представления информации.

Мощность алфавита – число символов в алфавите.

(записать определение в тетрадь)

Для того чтобы при измерении одной и той же информации получалось одно и то же значение количества информации, необходимо договориться об использовании определенного алфавита. Так как в технических системах применяется двоичный алфавит, то его же используют для измерения количества информации.

Количество знаков в алфавите N=2, N=2 i , I – количество информации, I = 3 бита.

N=2 i , где N – мощность алфавита, количество символов в алфавите,

i — информационный вес каждого символа, измеряется в битах. I – информационный объем текста, высчитывается по формуле. I=K*i, где К – количество символов в тексте.

Чем большее количество знаков в алфавите, тем большее количество информации несет 1 знак алфавита.

4. Физкультминутка. (1 мин.)

Раздаю детям карточки с единицами измерения информации, надо встать и собрать равенства.

5. Закрепление материала. Решение задач на определение количества информации.

№ 1. Определите самостоятельно количество информации, которое несет 1 буква русского алфавита.

Ответ: буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению информации).

№ 2. Два текста содержат одинаковое число символов. i=64

И находим i

В какой степени 2 будет равняться 64? В 6-ой степени)

И ответ- 6 бит

6. Подведение итогов урока в форме теста

— Какие существуют подходы к определению количества информации?

Ответ: существует 2 подхода к измерению количества информации – смысловой и технический или алфавитный.

— В чем состоит отличие одного подхода от другого?

Ответ: при смысловом подходе количество информации – мера уменьшения неопределенности знания при получении информационного сообщения, при алфавитном – количество знаков в сообщении * количество информации, которое несет 1 знак алфавита.

— Назовите единицы измерения информации от самых маленьких до самых больших.

Ответ: бит, байт, Кб, Мб, Гб, Тб.

— На какую величину отличается байт от Кб, Кб от Мб, Мб от Гб?

Ответ: 1024 (210).

— Сколько битов содержится в 1 байте?

Ответ: 8.

— Что такое бит при смысловом и алфавитном подходе к определению количества информации?

Ответ: при смысловом подходе бит – уменьшение неопределенности знания в 2 раза при получении информационного сообщения;

при алфавитном подходе бит – информационная емкость одного знака при двоичном кодировании.

7. Домашнее задание (3 мин.) (С.И.Семакин «Информатика. Базовый курс. 8 класс»)

1. Приведите примеры информационных сообщений, которые несут 1 бит информации.

Измерение — Группа по изучению уроков

Как правило, обучение и изучение каждого атрибута измерения состоит из четырех этапов: (1) прямое сравнение; (2) косвенное сравнение; (3) измерение в произвольных (нестандартных) единицах; и (4) измерение в стандартных единицах. В CCSS эти этапы четко описаны в преподавании и изучении линейных измерений от детского сада до 2-го класса. Однако учащиеся должны пройти эти этапы со всеми измеримыми атрибутами, даже если они могут тратить меньше времени на некоторые этапы, поскольку они приобретают больше опыта в измерениях. . Например, когда учащиеся узнают об объеме твердых тел в пятом классе, они, скорее всего, потратят гораздо меньше времени на первые три этапа по сравнению с тем, что они сделали, когда узнали о длине. Тем не менее, для студентов по-прежнему важно пройти эти этапы, чтобы они могли понять, что такое объем, процесс его измерения и как использовать инструменты для этого.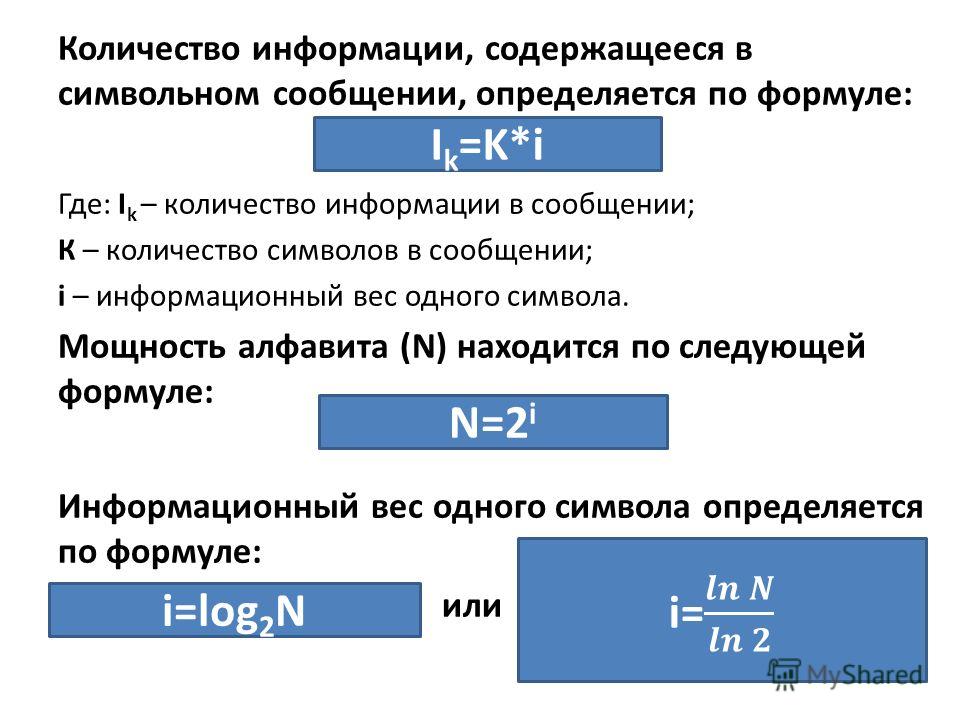

Стадия 1: Прямое сравнение

Итак, почему важно следовать этим четырем стадиям, когда мы начинаем наши инструкции по измерению? Основное внимание на первых двух этапах уделяется тому, чтобы помочь учащимся понять измеряемые атрибуты. В конце концов, прежде чем мы сможем что-то измерить, нам действительно нужно понять, что именно мы хотим измерить. Например, прежде чем мы сможем измерить длину, нам нужно понять, что такое длина. Поставив рядом два предмета (прямое сравнение), учащиеся могут определить, какой из них длиннее, а какой короче. Благодаря такому опыту учащиеся понимают, что длина — это расстояние между двумя концами объекта. (Хотя мы можем использовать разные слова, «высота» на самом деле не является атрибутом. Ее можно рассматривать как длину в вертикальной ориентации.) Конечно, посредством прямого сравнения учащиеся получают некоторое фундаментальное понимание того, как измерять объект. также. Например, при сравнении длин двух объектов важно, чтобы один конец объектов был выровнен.

Нельзя сказать, что верхний сегмент на рисунке ниже длиннее только потому, что он «выпирает» дальше вправо.

Учащиеся также узнают, что интересующее нас «пространство» находится на прямой траектории. Таким образом, мы не можем просто сравнить положения конечных точек, как показано на рисунке ниже.

Прежде чем мы сможем сравнить эти два объекта, конечные точки второго объекта должны быть расположены по прямой линии. Эти знания имеют основополагающее значение для понимания ребенком измерения.

Стадия

2: Косвенное сравнение

К сожалению, не всегда возможно прямое сравнение двух объектов. В ситуациях, когда это не так, иногда полезно использовать третий объект, который можно сравнивать непосредственно с каждым из двух объектов и действовать как ссылка между ними. Например, если один дверной проем шире размаха ваших рук, а другой уже, чем размах рук, вы знаете, что первый шире второго. Косвенное сравнение обеспечивает большую гибкость при сравнении двух объектов. Это также дает детям возможность испытать важное математическое свойство отношений, называемое транзитивностью. Это свойство утверждает, что если a > b и b > c, то a > c. Конечно, формальное изучение такого свойства произойдет гораздо позже.

Этап 3: Измерение с произвольными (нестандартными) Единицы

Возможно, более важной причиной обучения и изучения непрямого сравнения является то, что оно готовит почву для самой фундаментальной идеи о процессе измерения: использование единицы измерения . При использовании третьего объекта для косвенного сравнения его количество не всегда может быть промежуточным между количеством исходных двух объектов. Например, деревянная палка может быть намного короче обоих дверных проемов. Однако в этих случаях можно определить, что один дверной проем выше трех (одних и тех же) деревянных палочек, поставленных встык, а другой короче трех деревянных палочек. Теперь мы можем сказать, что первый дверной проем выше (длиннее), чем второй.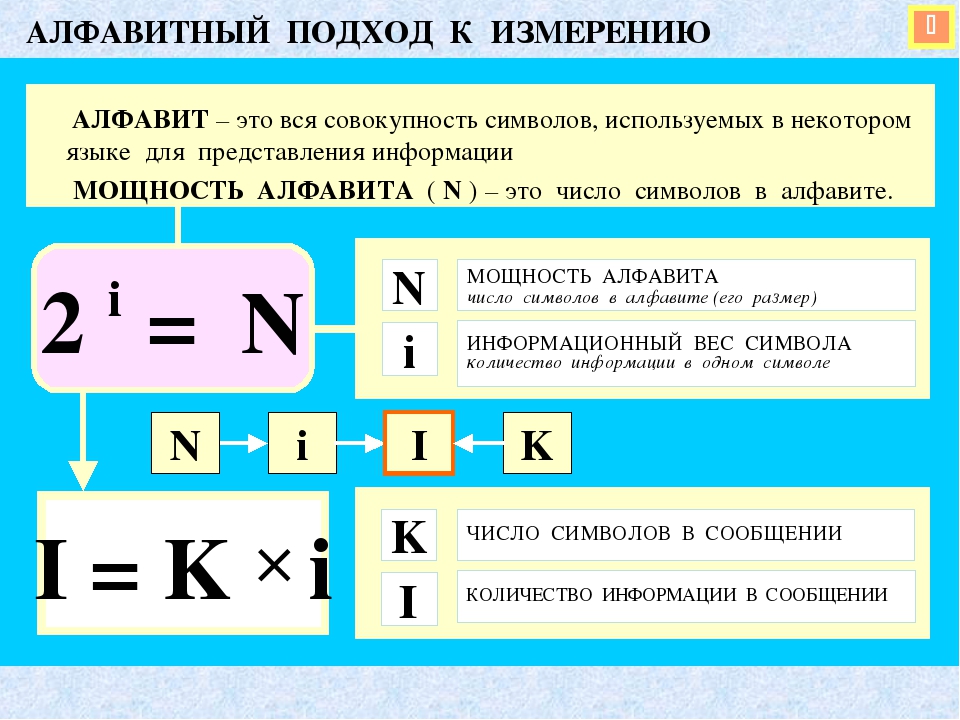

Нетрудно заметить, что такие переживания становятся основанием для идеи выражения признака через число третьего предмета, единицы, необходимого для его «покрытия». Когда мы переходим на эту стадию, мы теперь действительно «измеряем» в том смысле, что мы присваиваем номер объекту с точки зрения того, сколько атрибутов он имеет. Есть много преимуществ для выражения количества атрибута с помощью чисел. Ясно, что это упрощает процесс сравнения, поскольку нам больше не нужно находить разные объекты для использования в качестве эталона — сравнение нескольких объектов можно легко выполнить, просто сравнив числа одной установленной единицы. Еще одним важным преимуществом присвоения атрибутам чисел является то, что мы можем ответить не только на вопрос «что длиннее?» но и «на сколько?» В общем, как только мы выражаем количество атрибута числами, арифметические операции могут использоваться для ответа на более сложные вопросы. Несмотря на то, что CCSS прямо не заявляет об этих достоинствах, я надеюсь, что учителя помогут учащимся испытать и понять их.

Зачем

учить студентов использовать нестандартные единицы измерения?

Некоторые люди могут возразить, что, как только мы дойдем до этого этапа, мы должны просто использовать стандартные единицы измерения. Этот аргумент, возможно, имеет смысл позже, в начальных классах, когда учащиеся узнают об измерении трех или четырех различных атрибутов. Однако на уровне начального класса важно помнить, что учащиеся все еще изучают процесс измерения: выберите единицу измерения, затем определите, сколько итераций единицы необходимо, чтобы сравняться с атрибутом объекта, который вы измеряют. Для нас это так очевидно, а с детьми не так. Введение стандартных единиц на этом этапе потребует от детей одновременного изучения двух новых идей — новых единиц и нового процесса. Есть и другие соображения. Во-первых, некоторые единицы могут быть слишком маленькими или слишком большими, так что размер полученных чисел может не подходить для детей в данное время. Используя нестандартные единицы измерения, учителя могут контролировать диапазон чисел, которые могут получить учащиеся. Кроме того, важно отметить, что измерение в стандартных единицах обычно означает измерение с помощью различных инструментов. Например, если вы измеряете в дюймах, скорее всего, вы будете измерять линейкой. Однако обучение использованию линейки или любого измерительного инструмента также является сложной задачей само по себе — это может быть третьей новой идеей, с которой придется столкнуться учащимся, если мы введем стандартные единицы, не изучив нестандартные единицы .

Этап

Четвертый: измерение в стандартных единицах измерения

Хотя это может показаться немного парадоксальным, использование нестандартных единиц полезно для детей, чтобы понять необходимость наличия стандартных единиц. Например, если два ученика измерят ширину одного и того же дверного проема карандашами, они могут получить разные результаты. Этот тип опыта позволит им увидеть, что они не могут сравнивать числа, если их единицы измерения не совпадают. Именно тогда мы можем представить идею общих единиц, а затем, наконец, идею стандартных единиц, таких как дюймы, футы, сантиметры и метры.

Предварительная алгебра онлайн и планы уроков

Посмотрите наши демонстрации уроков!

Математика в восьмом классе обычно представляет собой курс предварительной алгебры, который помогает подготовить учащихся к алгебре в средней школе. Наша учебная программа по математике для 8-го класса может использоваться либо в качестве основной программы домашнего обучения, либо в качестве дополнения к другой учебной программе домашнего обучения или традиционной школе. Следующая информация объяснит, какие шаги вы должны предпринять, чтобы достичь целей и задач вашего ребенка по математике в 8-м классе, и как может помочь наша учебная программа по математике для 8-го класса.

Какую математику должен знать восьмиклассник?

Математическая программа для 8-го класса должна охватывать различные области математики, а не только арифметику. Основными разделами программы по математике для 8-го класса являются числовой смысл и операции, алгебра, геометрия и пространственный смысл, измерения, анализ данных и вероятность. Хотя эти математические направления могут вас удивить, все они являются важными уроками для математической программы 8-го класса.

Эти навыки улучшат беглость математики и помогут опираться на математические факты, концепции и стратегии, полученные в прошлом, что сделает будущие успехи более достижимыми. Вот некоторые темы, которые восьмиклассники уже должны знать по математике:

Запись чисел в словесной, стандартной, расширенной и экспоненциальной записи
Определение и использование соотношений и ставок
Умножение и деление положительных и отрицательных рациональных чисел
Нахождение периметра и площади двумерных фигур
Идентификация и построение упорядоченных пар в четырех квадрантах и вдоль осей
Расчет вероятностей независимых и зависимых событий

Если вашему учащемуся нужно повторить математические концепции 7-го класса, вы можете легко получить доступ к этим урокам благодаря нашим гибким параметрам уровня обучения, которые дают вам доступ на один уровень выше и на один ниже уровня по умолчанию для вашего ребенка.

Математические задачи для восьмого класса

Ниже приводится общий список некоторых целей обучения математике, которых должны достичь восьмиклассники:

Определите рациональные и иррациональные числа и опишите их значения.
Вычислить и аппроксимировать основные квадратные корни.
Определение и преобразование фигуры на координатной плоскости.
Решайте задачи с двумя переменными с помощью линейных уравнений.
Дайте определение и различие между различными типами методов выборки.
Используйте технологию для определения среднего значения, медианы, режима и диапазона набора реальных данных.

Математический прицел и последовательность для восьмиклассников

Глава 1. «Системы счисления»

Урок 1. Экспоненциальное представление

Выражайте числа от нуля до единицы в экспоненциальном представлении.

Урок 2. Рациональные и иррациональные числа

Определите рациональные и иррациональные числа и опишите их значения.

Урок 3. Абсолютное значение

Определите и объясните абсолютное значение.

Глава 2. Сравнение чисел и операций в экспоненциальном представлении.

Урок 2. Сравнение небольших чисел в экспоненциальном представлении

Сравнение небольших чисел в экспоненциальном представлении.

Урок 3. Сложение и вычитание чисел в экспоненциальном представлении

Сложение и вычитание чисел в экспоненциальном представлении.

Урок 4: Использование научной нотации с технологией

Использование научных обозначений с технологией

Глава 3: «Реальные числа»

Урок 1: Повторяя децималы на фракции

. дроби.

Урок 2. Корни

Вычисление и приближение главных квадратных корней.

Урок 3. Использование корней для решения уравнений

Использование корней для решения уравнений.

Урок 4.

Сравнение и упорядочивание

Сравнивайте и упорядочивайте числа во многих формах, включая дроби, десятичные дроби, экспоненциальное представление, абсолютное значение и радикалы.

Урок 5. Оценка

Используйте оценку для ситуаций, когда используются действительные числа.

Урок 6. Свойства

Применение свойств для решения задач с вещественными числами.

Урок 7. Операции с действительными числами

Упростите числовые выражения с помощью действительных чисел.

Глава 4. «Теория чисел»

Урок 1. Правила делимости

Используйте правила делимости для решения задач.

Урок 2. Множественные представления

Представление чисел в десятичной системе счисления в других системах счисления (двойке, пятерке и восьмерке) и наоборот.

Урок 3. Простые и составные числа

Определение чисел как относительно простых.

Глава 5: «Отношение, доля и процент»

Урок 1: Скорость изменения

Опишите и используйте скорость изменения для решения проблем.

Урок 2. Пропорции

Используйте отношения пропорциональности, чтобы найти меры длины, веса или массы, а также вместимости или объема.

Урок 3. Проценты

Решайте реальные задачи с процентами больше 100.

Глава 6. «Вычисления в реальном мире»

Урок 1. Операции

Решайте реальные задачи с рациональными числами (включая целые, десятичные дроби и дроби).

Урок 2: Реальные задачи

Решайте реальные задачи с отношениями, коэффициентами, пропорциями и процентами.

Урок 3. Многоэтапные задачи

Решайте реальные двух- или трехэтапные задачи с целыми числами, десятичными дробями, дробями, отношениями, долями, пропорциями и процентами.

Глава 7. Выражения и уравнения

Урок 2.

Выражения с показателями степени

Подставьте рациональные числа в выражения с показателями степени и радикалами.

Урок 3. Выражения и уравнения

Преобразование словесных выражений и уравнений в алгебраические выражения и уравнения (включая одну или несколько переменных и показателей степени).

Урок 4. Выражения, уравнения и неравенства

Перевод словесных выражений и предложений в алгебраические неравенства и наоборот.

Урок 5. Выражения в реальном мире

Используйте переменные для представления неизвестных величин в реальных ситуациях.

Урок 6. Упрощение

Объединяйте и упрощайте алгебраические выражения максимум с двумя переменными.

Урок 7. Подстановка

Вычисляйте алгебраические выражения и уравнения, подставляя целые значения вместо переменных и упрощая.

Урок 8. Неравенства

Алгебраически решать линейные неравенства с одной переменной.

Глава 8. «Нахождение решений и решение уравнений»

Урок 1. Определение количества решений линейного уравнения

Определение количества решений линейного уравнения.

Урок 2. Решение уравнений с переменными в обеих частях

Решите уравнения с переменными в обеих частях.

Урок 3. Решение уравнений, требующих распределительного свойства

Решите уравнения, требующие распределительного свойства.

Урок 4. Решение уравнений, требующих объединения одинаковых членов

Решите уравнения, требующие объединения одинаковых членов.

Глава 9: «Системы уравнений»

Урок 1: Анализ систем уравнений

Анализ систем уравнений.

Урок 2. Определение количества решений линейного уравнения

Определение количества решений линейного уравнения.

Глава 10. «Плоская геометрия»

Урок 1.

Геометрические свойства

Используйте свойства параллельности, перпендикулярности и симметрии для решения реальных задач.

Урок 2. Многоугольники

Сравните и опишите свойства выпуклых и вогнутых многоугольников.

Урок 3. Теорема Пифагора

Примените теорему Пифагора для решения реальных задач.

Урок 4. Соответствие и сходство

Определите сходство и сходство в реальных ситуациях и обосновайте.

Урок 5. Преобразования

Определение и выполнение преобразований (отражение, перемещение, вращение и расширение) фигуры на координатной плоскости.

Урок 6. Пропорциональные отношения

Определите, как изменения размеров влияют на площадь и периметр.

Глава 11. «Расширенные преобразования»

Урок 1. Преобразование линий и сегментов линий

Преобразование линий и сегментов линий.

Урок 2.

Преобразование углов

Преобразование углов.

Урок 3. Преобразование параллельных линий

Преобразование параллельных линий.

Урок 4. Понимание соответствия

Понимание соответствия.

Урок 5. Использование последовательности преобразований

Использование последовательности преобразований.

Урок 6. Понимание похожих фигур

Понимание похожих фигур.

Урок 7. Описание последовательностей трансформаций, демонстрирующих сходство

Опишите последовательности трансформаций, которые показывают сходство.

Глава 12. «Треугольники»

Урок 1. Неформальное доказательство теорем о треугольниках

Неформальное доказательство теорем о треугольниках.

Урок 2. Понимание углов, образующихся при пересечении параллельных прямых секущей

Понимание углов, образующихся при пересечении параллельных прямых секущей.

Урок 3. Исследование подобия углов

Исследуйте сходство углов.

Глава 13. «Расширенная теорема Пифагора»

Урок 1. Использование обратной теоремы Пифагора

Используйте обратную теорему Пифагора.

Урок 2. Применение теоремы Пифагора в трех измерениях

Применение теоремы Пифагора в трех измерениях.

Урок 3: Применение теоремы Пифагора в координатной плоскости

Примените теорему Пифагора в координатной плоскости.

Глава 14. «Трехмерная геометрия»

Урок 1. Объем

Найдите объем пирамид, призм и конусов.

Урок 2. Применение формул объема

Применение формул объема.

Урок 3. Площадь поверхности

Найдите площадь поверхности пирамид, призм и конусов.

Урок 4. Правильные и неправильные многоугольники

Сравните правильные и неправильные многоугольники.

Урок 5. Измерение угла

Нахождение меры угла в двумерных фигурах и двухмерных сторонах трехмерных фигур на основе геометрических соотношений.

Урок 6. Соотношения пропорциональности

Определите взаимосвязь между объемом или площадью поверхности и размером.

Глава 15. «Измерение»

Урок 1. Масштаб

Интерпретация и применение различных масштабов, включая числовые линии, графики, модели и карты.

Урок 2: Оценка

Выбрать инструменты для измерения величин и размеров с заданной степенью точности и определить максимально возможную погрешность измерения.

Урок 3. Значащие цифры

Определите количество значащих цифр по отношению к наименее точной единице измерения и примените их к реальным условиям.

Глава 16. «Построение графиков»

Урок 1. Таблицы и упорядоченные пары

Урок 2. Уравнения для линий

Графики линейных уравнений в стандартной форме.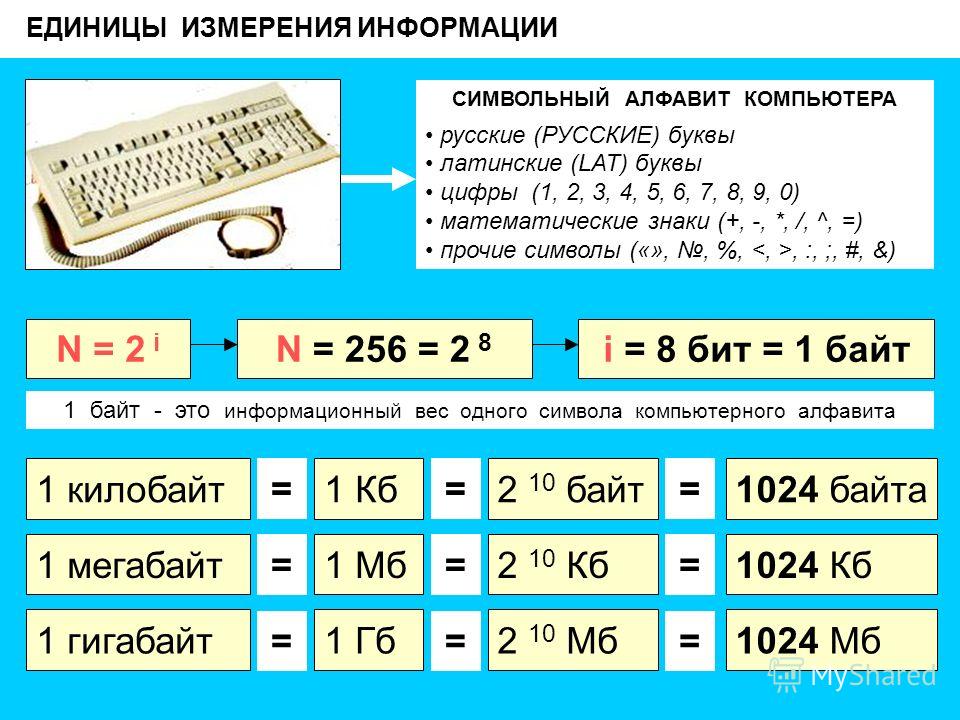

Урок 3. Линейные неравенства

Определение и графическое отображение неравенств на числовой прямой.

Урок 4. Неравенства

Определение и графическое отображение неравенств в координатной плоскости.

Урок 5. Применение линейных неравенств

Решение задач с двумя переменными с помощью линейных неравенств. Глава 17: «Линейные зависимости»

Урок 2. Наклон линии

По графику линии определить наклон.

Урок 3. Запись уравнений в форме наклона и точки пересечения

Учитывая наклон и точку пересечения по оси Y, напишите уравнение.

Урок 4. Поиск правила функции

Найдите правило функции для описания линейной зависимости с помощью таблиц связанных входных и выходных переменных.

Урок 5. Определение линейности функции

Используя информацию из таблицы, графика или правила, определите, является ли функция линейной, и выровняйте ее.

Глава 18. «Понимание, использование и интерпретация уклона»

Урок 1. Отображение пропорциональных отношений и интерпретация уклона

Графики пропорциональных отношений и интерпретация уклона.

Урок 2. Использование похожих треугольников для определения уклона

Использование подобных треугольников для определения уклона.

Урок 3. Использование формы пересечения наклона

Используйте форму пересечения наклона.

Урок 4. Интерпретация y = mx + b как линейной функции

Интерпретация y = mx + b как линейной функции.

Глава 19. «Функции»

Урок 1. Распознавание функций

Распознавание функций.

Урок 2. Сравнение функций, представленных в разных формах

Сравните функции, представленные в разных формах.

Урок 3. Интерпретация y = mx + b как линейной функции

Интерпретируйте y = mx + b как линейную функцию.

Урок 4. Построение линейных функций

Построение линейных функций.

Урок 5. Описание функциональной связи с помощью анализа графика

Описание функциональной связи с помощью анализа графика.

Урок 6. Рисование графиков функций

Графики функций.

Глава 20: «Вероятность»

Урок 1. Условная вероятность

Расчет условных вероятностей и вероятностей зависимых событий.

Урок 2. Методы выборочного контроля

Дайте определение и различие между различными типами методов выборочного контроля.

Урок 3. Применение выборки

Используйте различные методы выборки для сбора данных.

Урок 4. Выборочная погрешность

Определите, является ли выборка необъективной.